2021 VCE Further Maths Exam 2
This is the full VCE Further Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 60
Reading time: 15 minutes
Writing time: 1.5 hours
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
SECTION A – Core
Data analysis
In the sport of heptathlon, athletes compete in seven events.
These events are the 100 m hurdles, high jump, shot-put, javelin, 200 m run, 800 m run and long jump.
Fifteen female athletes competed to qualify for the heptathlon at the Olympic Games.
Their results for three of the heptathlon events – high jump, shot-put and javelin – are shown in Table 1.
Table 1
| Athlete number | High jump (metres) | Shot-put (metres) | Javelin (metres) |
|---|---|---|---|
| 1 | 1.76 | 15.34 | 41.22 |
| 2 | 1.79 | 16.96 | 42.41 |
| 3 | 1.83 | 13.87 | 46.53 |
| 4 | 1.82 | 14.23 | 40.62 |
| 5 | 1.87 | 13.78 | 45.64 |
| 6 | 1.73 | 14.50 | 42.33 |
| 7 | 1.68 | 15.08 | 40.88 |
| 8 | 1.82 | 13.13 | 39.22 |
| 9 | 1.83 | 14.22 | 42.51 |
| 10 | 1.87 | 13.62 | 42.75 |
| 11 | 1.87 | 12.01 | 38.12 |
| 12 | 1.80 | 12.88 | 42.65 |
| 13 | 1.83 | 12.68 | 45.68 |
| 14 | 1.87 | 12.45 | 41.32 |
| 15 | 1.78 | 11.31 | 42.88 |
a. Write down the number of numerical variables in Table 1. 1 mark
b. Complete Table 2 below by calculating the mean height jumped for the high jump, in metres, by the 15 athletes. Write your answer in the space provided in the table. 1 mark
Table 2
| Statistic | High jump (metres) | Shot-put (metres) |
|---|---|---|
| mean | 13.74 | |
| standard deviation | 0.06 | 1.43 |
c. In shot-put, athletes throw a heavy spherical ball (a shot) as far as they can.
Athlete number six, Jamilia, threw the shot 14.50 m.
Calculate Jamilia’s standardised score (z).
Round your answer to one decimal place. 1 mark
d. In the qualifying competition, the heights jumped in the high jump are expected to be approximately normally distributed.
Chara’s jump in this competition would give her a standardised score of \(z = -1.0\)
Use the 68–95–99.7% rule to calculate the percentage of athletes who would be expected to jump higher than Chara in the qualifying competition. 1 mark
e. The boxplot below was constructed to show the distribution of high jump heights for all 15 athletes in the qualifying competition.
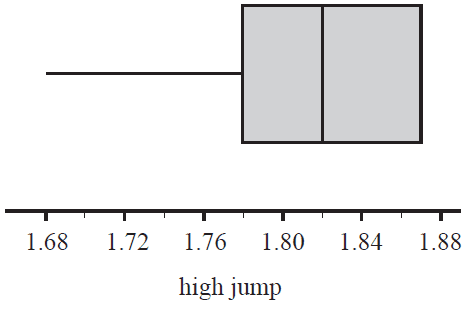
Explain why the boxplot has no whisker at its upper end. 1 mark
f. For the javelin qualifying competition (refer to Table 1 on page 2), another boxplot is used to display the distribution of athletes’ results.
An athlete whose result is displayed as an outlier at the upper end of the plot is considered to be a potential medal winner in the event.
What is the minimum distance that an athlete needs to throw the javelin to be considered a potential medal winner? 2 marks
The two running events in the heptathlon are the 200 m run and the 800 m run. The times taken by the athletes in these two events, time200 and time800, are linearly related.
When a least squares line is fitted to the data, the equation of this line is found to be
\( \textit{time800} = 0.03931 + 5.2756 \times \textit{time200} \)
a. Round the values for the intercept and the slope to three significant figures. Write your answers in the boxes provided. 1 mark
\( \textit{time800} = \) \( + \) \( \times \textit{time200} \)
b. The mean and the standard deviation for each variable, time200 and time800, are shown in the table below.
| Statistic | Time200 (seconds) | Time800 (seconds) |
|---|---|---|
| mean | 24.6492 | 136.054 |
| standard deviation | 0.96956 | 8.2910 |
The equation of the least squares line is
\( \textit{time800} = 0.03931 + 5.2756 \times \textit{time200} \)
Use this information to calculate the coefficient of determination as a percentage.
Round your answer to the nearest percentage. 2 marks
The time series plot below shows the winning time, in seconds, for the women's 100 m freestyle swim plotted against year, for each year that the Olympic Games were held during the period 1956 to 2016.
A least squares line has been fitted to the plot to model the decreasing trend in the winning time over this period.
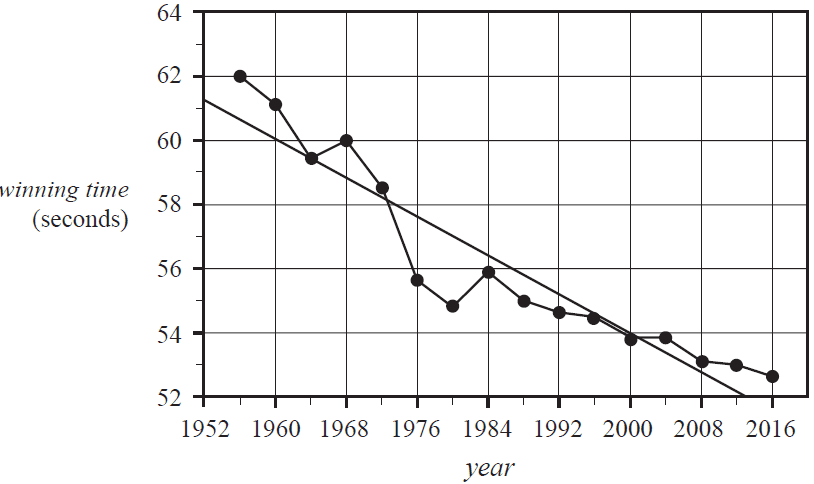
The equation of the least squares line is
\( \textit{winning time} = 357.1 - 0.1515 \times \textit{year} \)
The coefficient of determination is 0.8794
a. Name the explanatory variable in this time series plot. 1 mark
b. Determine the value of the correlation coefficient (\(r\)).
Round your answer to three decimal places. 1 mark
c. Write down the average decrease in winning time, in seconds per year, during the period 1956 to 2016. 1 mark
d. The predicted winning time for the women's 100 m freestyle in 2000 was 54.10 seconds.
The actual winning time for the women's 100 m freestyle in 2000 was 53.83 seconds.
Determine the residual value in seconds. 1 mark
e. The following equation can be used to predict the winning time for the women's 100 m freestyle in the future.
\( \textit{winning time} = 357.1 - 0.1515 \times \textit{year} \)
i. Show that the predicted winning time for the women's 100 m freestyle in 2032 is 49.252 seconds. 1 mark
ii. What assumption is being made when this equation is used to predict the winning time for the women's 100 m freestyle in 2032? 1 mark
The time series plot below shows that the winning time for both men and women in the 100 m freestyle swim in the Olympic Games has been decreasing during the period 1912 to 2016.
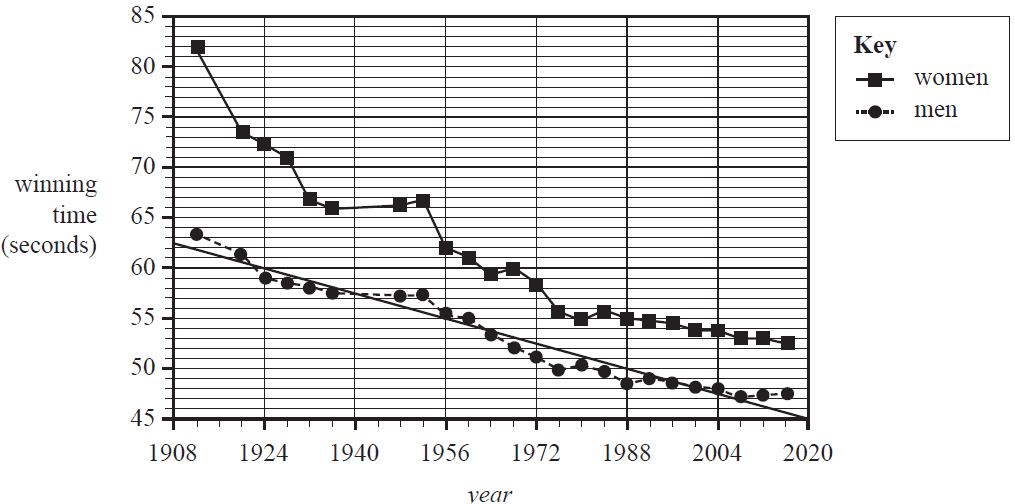
Least squares lines are used to model the trend for both men and women.
The least squares line for the men’s winning time has been drawn on the time series plot above.
The equation of the least squares line for men is
\( \textit{winning time men} = 356.9 - 0.1544 \times \textit{year} \)
The equation of the least squares line for women is
\( \textit{winning time women} = 538.9 - 0.2430 \times \textit{year} \)
a. Draw the least squares line for winning time women on the time series plot above. 1 mark
(Answer on the time series plot above.)
b. The difference between the women’s predicted winning time and the men’s predicted winning time can be calculated using the formula
\( \textit{difference} = \textit{winning time women} - \textit{winning time men} \)
Use the equations of the least squares lines on page 8 and the formula above to calculate the difference predicted for the 2024 Olympic Games.
Round your answer to one decimal place. 2 marks
c. The Olympic Games are held every four years. The next Olympic Games will be held in 2024, then 2028, 2032 and so on.
In which Olympic year do the two least squares lines predict that the winning time for women will first be faster than the winning time for men in the 100 m freestyle? 2 marks
A method for predicting future time differences in the 100 m freestyle swim is to use the formula
\( \textit{difference} = \textit{winning time women} - \textit{winning time men} \)
The resulting data and time series plot are shown below. The plot is clearly non-linear.
| Year | Difference (seconds) |
|---|---|
| 1912 | 18.8 |
| 1920 | 12.2 |
| 1924 | 13.4 |
| 1928 | 12.4 |
| 1932 | 8.6 |
| 1936 | 8.3 |
| 1948 | 9.0 |
| 1952 | 9.4 |
| 1956 | 6.6 |
| 1960 | 6.0 |
| 1964 | 6.1 |
| 1968 | 7.8 |
| 1972 | 7.4 |
| 1976 | 5.7 |
| 1980 | 4.4 |
| 1984 | 6.1 |
| 1988 | 6.3 |
| 1992 | 5.6 |
| 1996 | 5.8 |
| 2000 | 5.5 |
| 2004 | 5.7 |
| 2008 | 5.9 |
| 2012 | 5.5 |
| 2016 | 5.1 |
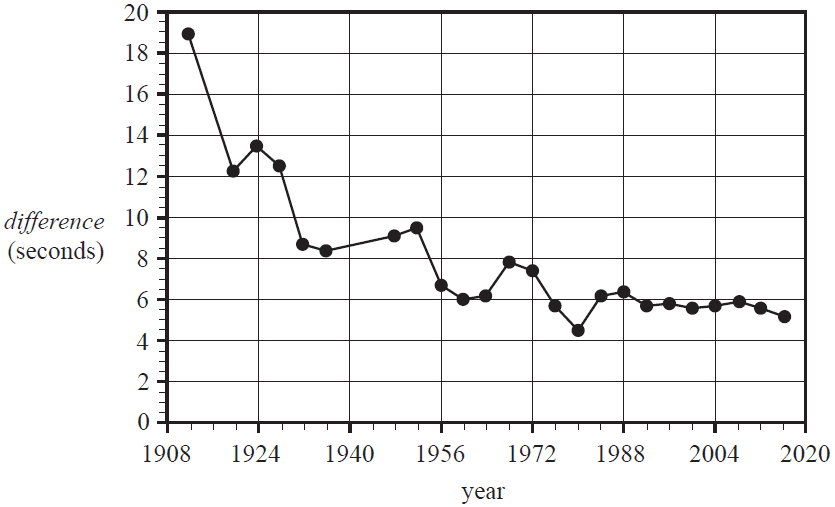
a. Apply a reciprocal transformation to the variable difference to linearise the data. Fit a least squares line to the transformed data and write its equation below.
Round the values of the intercept and the slope to four significant figures. 2 marks
b. Use the equation from part a. to predict, in seconds, the difference between the women's and men's winning times in the year 2032.
Round your answer to one decimal place. 1 mark
Recursion and financial modelling
Sienna invests $420 000 in a perpetuity from which she will receive a regular monthly payment of $1890.
The perpetuity earns interest at the rate of 5.4% per annum.
a. Determine the total amount, in dollars, that Sienna will receive after one year of monthly payments. 1 mark
b. Write down the value of the perpetuity after Sienna has received one year of monthly payments. 1 mark
c. Let \(S_n\) be the value of Sienna's perpetuity after \(n\) months.
Complete the recurrence relation, in terms of \(S_0\), \(S_{n+1}\) and \(S_n\), that would model the value of this perpetuity over time. Write your answers in the boxes provided. 1 mark
\(S_0 = \) , \(S_{n+1} = \) \( \times S_n - 1890 \)
Sienna owns a coffee shop.
A coffee machine, purchased for $12 000, is depreciated in value using the unit cost method.
The rate of depreciation is $0.05 per cup of coffee made.
The recurrence relation that models the year-to-year value, in dollars, of the coffee machine is
\(M_0 = 12\,000, \quad M_{n+1} = M_n - 1440\)
a. Calculate the number of cups of coffee that the machine produces per year. 1 mark
b. The recurrence relation above could also represent the value of the coffee machine depreciating at a flat rate.
What annual flat rate percentage of depreciation is represented? 1 mark
c. Complete the rule below that gives the value of the coffee machine, \(M_n\), in dollars, after \(n\) cups have been produced. Write your answers in the boxes provided. 1 mark
\(M_n = \) \( + \) \( \times n \)
For renovations to the coffee shop, Sienna took out a reducing balance loan of $570 000 with interest calculated fortnightly.
The balance of the loan, in dollars, after \(n\) fortnights, \(S_n\), can be modelled by the recurrence relation
\(S_0 = 570\,000, \quad S_{n+1} = 1.001S_n - 1193\)
a. Calculate the balance of this loan after the first fortnightly repayment is made. 1 mark
b. Show that the compound interest rate for this loan is 2.6% per annum. 1 mark
c. For the loan to be fully repaid, to the nearest cent, Sienna’s final repayment will be a larger amount.
Determine this final repayment amount.
Round your answer to the nearest cent. 1 mark
Sienna invests $152 431 into an annuity from which she will receive a regular monthly payment of $900 for 25 years. The interest rate for this annuity is 5.1% per annum, compounding monthly.
a. Let \(V_n\) be the balance of the annuity after \(n\) monthly payments. A recurrence relation written in terms of \(V_0\), \(V_{n+1}\) and \(V_n\) can model the value of this annuity from month to month.
Showing recursive calculations, determine the value of the annuity after two months.
Round your answer to the nearest cent. 2 marks
b. After two years, the interest rate for this annuity will fall to 4.6%.
To ensure that she will still receive the same number of $900 monthly payments, Sienna will add an extra one-off amount into the annuity at this time.
Determine the value of this extra amount that Sienna will add.
Round your answer to the nearest cent. 1 mark
SECTION B – Modules
Module 1 – Matrices
Elena imports three brands of olive oil: Carmani (C), Linelli (L) and Ohana (O).
The number of 1 litre bottles of these oils sold in January 2021 is shown in matrix \(J\) below.
\[ J = \begin{bmatrix} 2800 \\ 1700 \\ 2400 \end{bmatrix} \begin{matrix} C \\ L \\ O \end{matrix} \]
a. What is the order of matrix \(J\)? 1 mark
b. Elena expected that in February 2021 the sales of all three brands of olive oil would increase by 5%.
She multiplied matrix \(J\) by a scalar value, \(k\), to determine the expected volume of sales for February.
Write down the value of the scalar \(k\). 1 mark
\(k = \)
The main computer system in Elena's office has broken down.
The five staff members, Alex (A), Brie (B), Chai (C), Dex (D) and Elena (E), are having problems sending information to each other.
Matrix \(M\) below shows the available communication links between the staff members.

In this matrix:
- the '1' in row \(A\), column \(B\) indicates that Alex can send information to Brie
- the '0' in row \(D\), column \(C\) indicates that Dex cannot send information to Chai.
a. Which two staff members can send information directly to each other? 1 mark
b. Elena needs to send documents to Chai.
What is the sequence of communication links that will successfully get the information from Elena to Chai? 1 mark
c. Matrix \(M^2\) below is the square of matrix \(M\) and shows the number of two-step communication links between each pair of staff members.

Only one pair of individuals has two different two-step communication links.
List each two-step communication link for this pair. 1 mark
A market research study of shoppers showed that the buying preferences for the three olive oils, Carmani (C), Linelli (L) and Ohana (O), change from month to month according to the transition matrix \(T\) below.
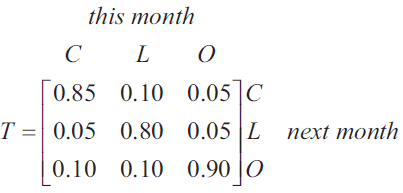
The initial state matrix \(S_0\) below shows the number of shoppers who bought each brand of olive oil in July 2021.
\[ S_0 = \begin{bmatrix} 3200 \\ 2000 \\ 2800 \end{bmatrix} \begin{matrix} C \\ L \\ O \end{matrix} \]
Let \(S_n\) represent the state matrix describing the number of shoppers buying each brand \(n\) months after July 2021.
a. How many of these 8000 shoppers bought a different brand of olive oil in August 2021 from the brand bought in July 2021? 1 mark
b. Using the rule \(S_{n+1} = T \times S_n\), complete the matrix \(S_1\) below. 1 mark
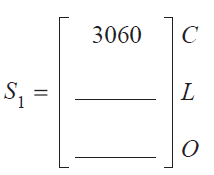
c. Consider the shoppers who were expected to buy Carmani olive oil in August 2021.
What percentage of these shoppers also bought Carmani olive oil in July 2021?
Round your answer to the nearest percentage. 1 mark
d. Write a calculation that shows that Ohana olive oil is the brand bought by 50% of these shoppers in the long run. 1 mark
e. Further research suggests more shoppers will buy olive oil in the coming months.
A rule to model this situation is \(R_{n+1} = T \times R_n + B\), where \(R_n\) represents the state matrix describing the number of shoppers \(n\) months after July 2021.
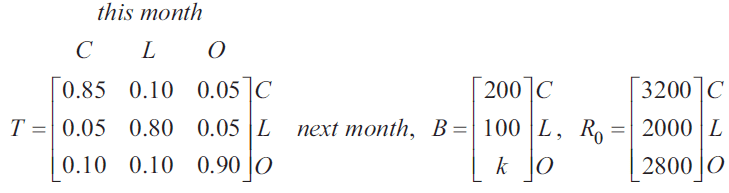
\(k\) represents the extra number of shoppers expected to buy Ohana olive oil each month.
If \(R_2 = \begin{bmatrix} 3333 \\ 2025 \\ 3642 \end{bmatrix}\), what is the value of \(k\)? 1 mark
Five staff members in Elena's office played a round-robin video game tournament, where each employee played each of the other employees once. In each game there was a winner and a loser.
A table of their one-step and two-step dominances was prepared to summarise the results.
| Staff member | One-step dominance | Two-step dominance |
|---|---|---|
| Ike (I) | 3 | 5 |
| Joelene (J) | 3 | 4 |
| Katie (K) | 1 | 1 |
| Leslie (L) | 1 | 2 |
| Mikki (M) | 2 | 4 |
Consider the results matrix shown below.
A '1' in this matrix shows that the player named in that row defeated the player named in that column.
A '0' in this matrix shows that the player named in that row lost to the player named in that column.
Use all of the information provided to complete the results matrix. 2 marks

Module 2 – Networks and decision mathematics
Maggie's house has five rooms, A, B, C, D and E, and eight doors.
The floor plan of these rooms and doors is shown below. The outside area, F, is shown shaded on the floor plan.
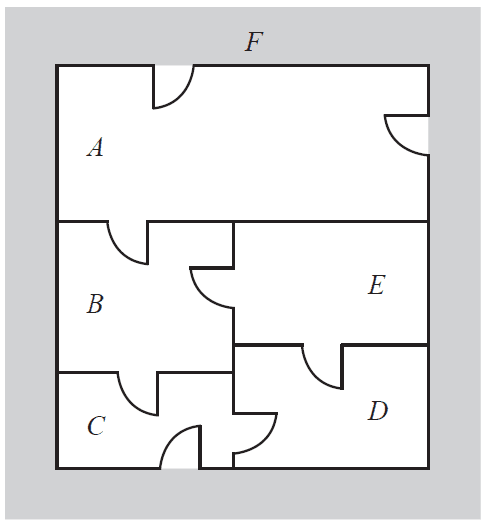
The floor plan is represented by the graph below.
On this graph, vertices represent the rooms and the outside area. Edges represent direct access to the rooms through the doors.
One edge is missing from the graph.
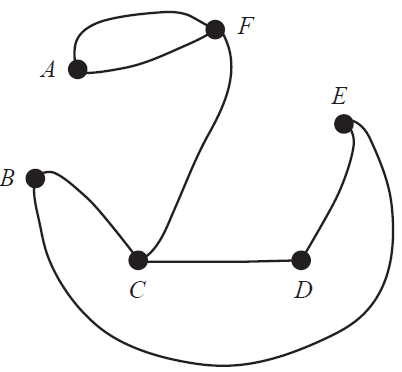
a. On the graph above, draw the missing edge. 1 mark
(Answer on the graph above.)
b. What is the degree of vertex E? 1 mark
c. Maggie hires a cleaner to clean the house.
It is possible for the cleaner to enter the house from the outside area, F, and walk through each room only once, cleaning each room as he goes and finishing in the outside area, F.
i. Complete the following to show one possible route that the cleaner could take. 1 mark
F – – – – – F
ii. What is the mathematical term for such a journey? 1 mark
George lives in Town G and Maggie lives in Town M.
The diagram below shows the network of main roads between Town G and Town M.
The vertices G, H, I, J, K, L, M, N and O represent towns.
The edges represent the main roads. The numbers on the edges indicate the distances, in kilometres, between adjacent towns.
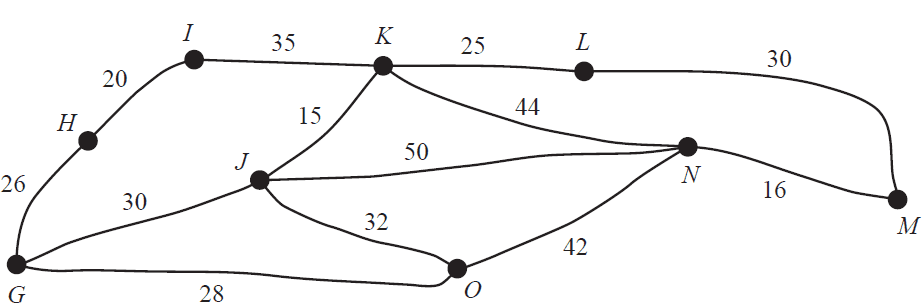
a. What is the shortest distance, in kilometres, between Town G and Town M? 1 mark
b. George plans to travel to Maggie's house. He will pass through all the towns shown above.
George plans to take the shortest route possible.
Which town will George pass through twice? 1 mark
The network diagram below shows the local road network of Town M.
The numbers on the edges indicate the maximum number of vehicles per hour that can travel along each road in this network.
The arrows represent the permitted direction of travel.
The vertices A, B, C, D, E and F represent the intersections of the roads.
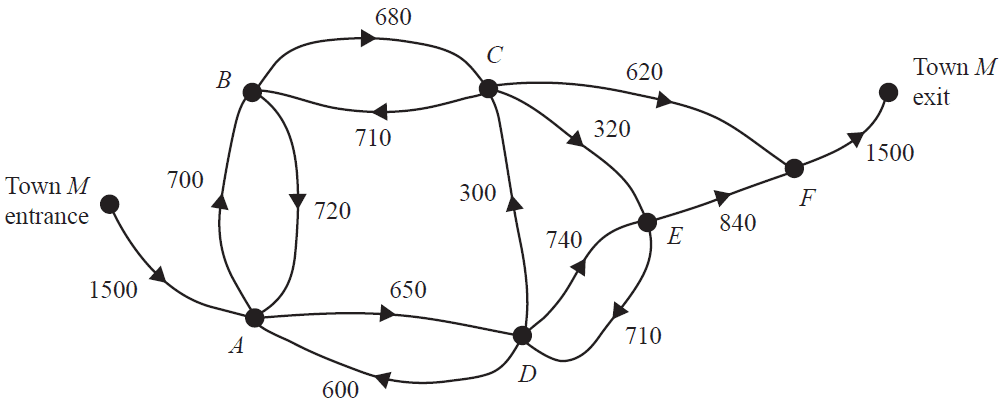
a. Determine the maximum number of vehicles that can travel from the entrance to the exit per hour. 1 mark
b. The local council plans to increase the number of vehicles per hour that can travel from the entrance to the exit by increasing the capacity of only one road.
i. Complete the following sentence by filling in the boxes provided. 1 mark
The road that should have its capacity increased is the road from vertex to vertex .
ii. What should be the minimum capacity of this road to maximise the flow of vehicles from the entrance to the exit? 1 mark
Roadworks planned by the local council require 13 activities to be completed.
The network below shows these 13 activities and their completion times in weeks.
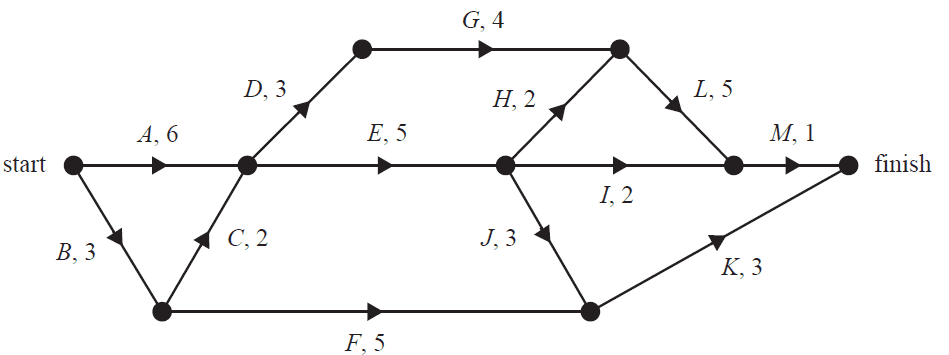
a. What is the earliest start time, in weeks, of activity K? 1 mark
b. How many of these activities have zero float time? 1 mark
c. It is possible to reduce the completion time for activities A, E, F, L and K.
The reduction in completion time for each of these five activities will incur an additional cost.
The table below shows the five activities that can have their completion time reduced and the associated weekly cost, in dollars.
| Activity | Weekly cost ($) |
|---|---|
| A | 140 000 |
| E | 100 000 |
| F | 100 000 |
| L | 120 000 |
| K | 80 000 |
The completion time for each of these five activities can be reduced by a maximum of two weeks.
The overall completion time for the roadworks can be reduced to 16 weeks.
What is the minimum cost, in dollars, of this change in completion time? 1 mark
Module 3 – Geometry and measurement
The game of squash is played with a spherical ball that has a radius of 2 cm.
a. Show that the volume of one squash ball, rounded to two decimal places, is 33.51 cm³. 1 mark
Squash balls may be sold in cube-shaped boxes.
Each box contains one ball and has a side length of 4.1 cm, as shown in the diagram below.
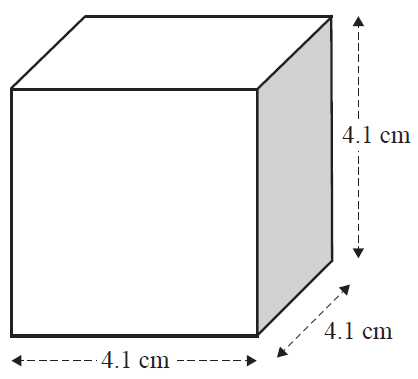
b. Calculate the empty space, in cubic centimetres, that surrounds the ball in the box.
Round your answer to two decimal places. 1 mark
c. Calculate the total surface area, in square centimetres, of one box. 1 mark
d. Retail shops store the cube-shaped boxes in a space within a display unit.
The space has a length of 17.0 cm and a width of 12.5 cm. Due to the presence of a shelf above, there is a maximum height of 8.5 cm available. This is shown in the diagram below.
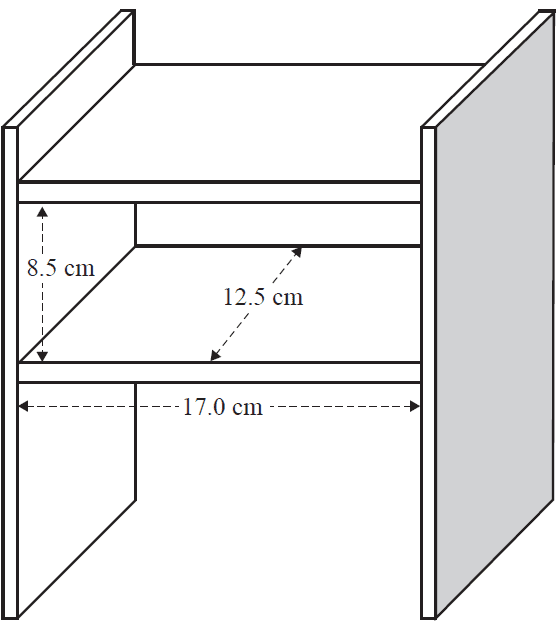
Calculate the maximum number of cube-shaped boxes that can fit into the space within the display unit. 1 mark
The game of squash is played indoors on a court with a front wall, a back wall and two side walls, as shown in the image below.

Each side wall has the following dimensions.
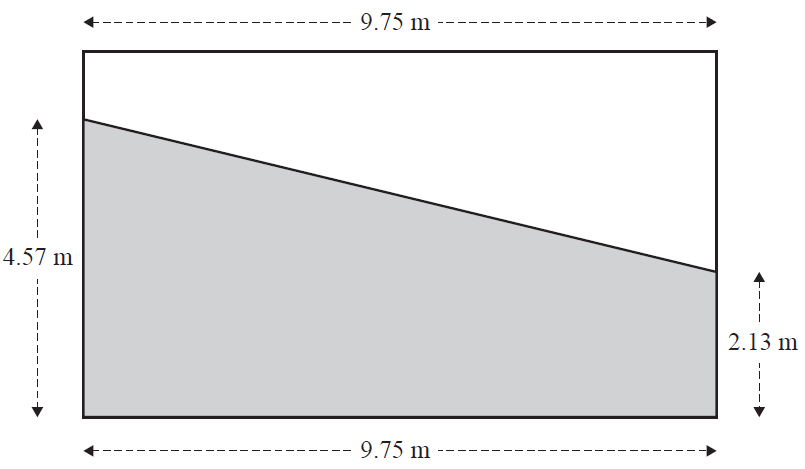
The shaded region in the diagram above is considered part of the playing area.
a. Calculate the area, in square metres, of the shaded region in the diagram above.
Round your answer to two decimal places. 1 mark
b. Calculate the perimeter, in metres, of the shaded region in the diagram on page 28.
Round your answer to one decimal place. 1 mark
c. Two squash players, Wei-Yi and Bao, are playing a match.
The diagram below shows the lines on the court floor.
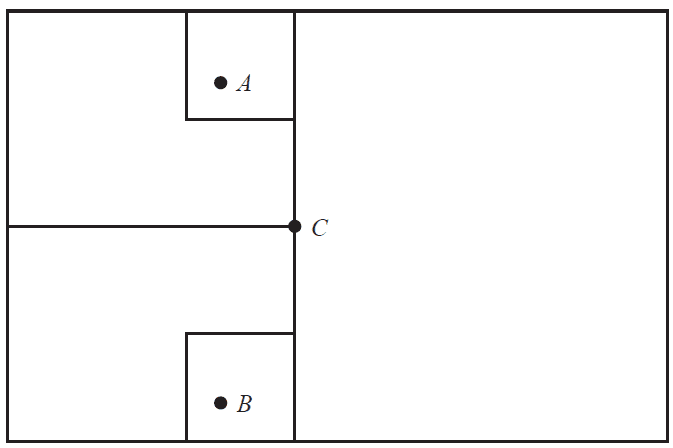
Wei-Yi is serving from point A and Bao is standing at point B.
Point A is 2.7 m from Point C.
Point B is 3.1 m from Point C.
The angle ACB is 119°.
Show that the distance between Wei-Yi and Bao is 5 m, rounded to the nearest metre. 1 mark
Players will travel from around the world to a squash competition in New York City (41° N, 74° W).
The top three female players are from three different cities:
- Wei-Yi is from Shanghai (31° N, 121° E) in China.
- Camilla is from Durban (30° S, 31° E) in South Africa.
- Ozlem is from Istanbul (41° N, 29° E) in Turkey.
a. Which players are from the Northern Hemisphere? 1 mark
The diagram below shows the locations of Shanghai, Durban and New York City.
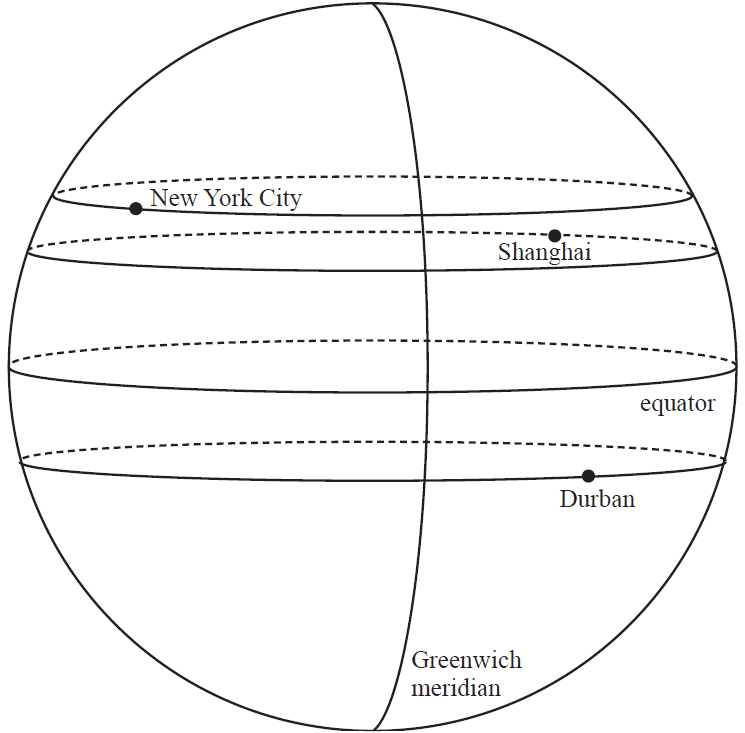
b. The city of Istanbul (41° N, 29° E) is missing from the diagram.
On the diagram above, mark with an ‘X’ the location of Istanbul. 1 mark
(Answer on the diagram above.)
c. The flight from Istanbul (41° N, 29° E) to New York City (41° N, 74° W) travels along a small circle. Assume that the radius of Earth is 6400 km.
i. Show that the radius of this small circle, rounded to the nearest kilometre, is 4830. 1 mark
ii. Calculate the distance that the plane travels between Istanbul (41° N, 29° E) and New York City (41° N, 74° W).
Round your answer to the nearest kilometre. 1 mark
d. Wei-Yi and Camilla both arrive in New York City on Monday 11 January at 10.00 pm, local time.
Wei-Yi’s flight left Shanghai on Monday 11 January at 8.00 pm, local time.
Camilla’s flight left Durban on Monday 11 January at 4.00 am, local time.
Assume that the time difference between Shanghai and New York City is 13 hours, and that the time difference between Durban and New York City is seven hours.
How much longer, in hours, was Camilla’s flight compared to Wei-Yi’s flight? 1 mark
Module 4 – Graphs and relations
The graph below shows the height, in metres, of a drone flying above a new housing estate over a six-minute period of time.
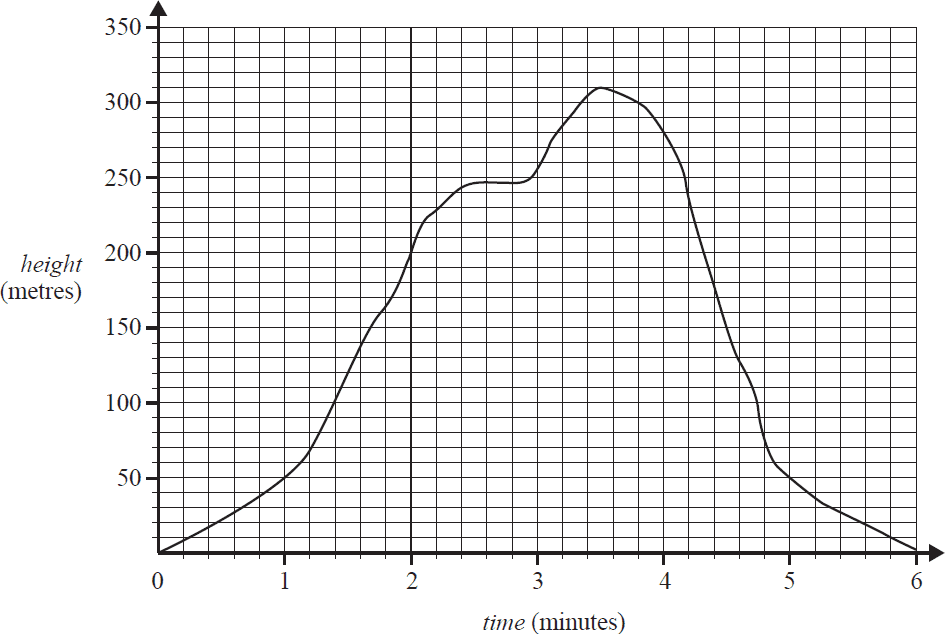
a. For what length of time, in minutes, was the height of the drone at least 50 m? 1 mark
b. What was the average rate of change in the height of the drone, in metres per minute, in the first two minutes? 1 mark
Christy sells blocks of land at the housing estate.
Her pay is based on the number of blocks that she sells each week.
The maximum number of blocks sold each week is 20.
The graph below shows Christy's weekly pay, in dollars, for the number of blocks sold.
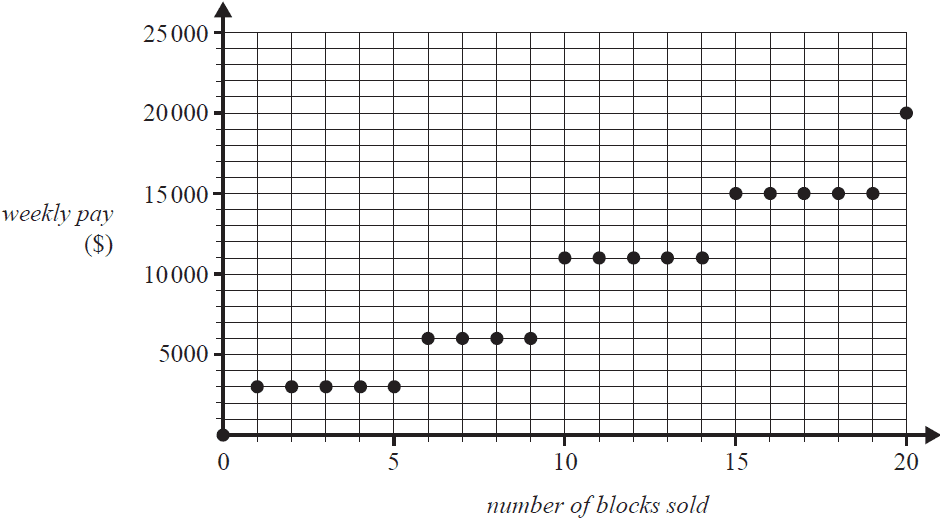
a. What is the minimum number of blocks of land that Christy must sell to receive $6000 in one week? 1 mark
John also sells blocks of land. He is paid $1000 for each block that he sells.
b. Write down all values for the number of blocks of land sold for which Christy and John will receive the same weekly pay. 1 mark
c. John sells no more than three blocks of land for every five blocks of land sold by Christy.
Let \(x\) be the number of blocks that Christy sells.
Let \(y\) be the number of blocks that John sells.
An inequality written as \(y\) in terms of \(x\) can represent this situation.
Complete this inequality in the box below. 1 mark
\(y\)
Lam is a builder constructing a community centre at the new housing estate.
The cost, \(C\), in dollars, for Lam to work onsite for \(n\) weeks is given by
\(C = 10\,000 + k \times n\)
a. The cost of 15 weeks of onsite work is $92 500.
Show that the value of \(k\) is 5500. 1 mark
Lam's revenue for this job is $6500 per week.
b. Determine the number of weeks that Lam needs to work onsite to break even. 1 mark
c. An equation for the profit, \(P\), in dollars, made by Lam in terms of the number of weeks worked onsite, \(n\), can be determined.
Complete this equation by filling in the boxes below. 1 mark
\( P = \) \( \times n + \)
Health and training sessions are held each day at the new community centre.
- Let \(x\) be the number of sessions for children each day.
- Let \(y\) be the number of sessions for adults each day.
- The total number of all sessions each day must be at least 10.
- The number of sessions for adults must not be less than the number of sessions for children.
- It takes 30 minutes for each session for children and 40 minutes for each session for adults.
The constraints on the health and training sessions each day can be represented by the following five inequalities.
Inequality 1 \(x \ge 0\)
Inequality 2 \(y \ge 0\)
Inequality 3 \(x + y \ge 10\)
Inequality 4 \(y \ge x\)
Inequality 5 \(30x + 40y \le 600\)
a. Explain the meaning of Inequality 5 in the context of this situation. 1 mark
The graph below shows the feasible region (shaded) that satisfies Inequalities 1 to 5.
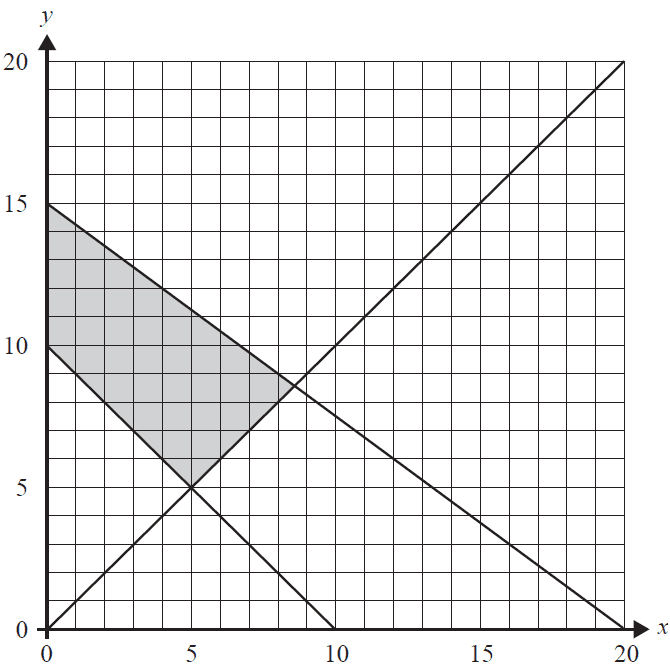
b. What is the maximum number of sessions for children each day? 1 mark
c. The community profits from these sessions.
Each session for children makes a profit of $45 and each session for adults makes a profit of $60.
i. Determine the maximum profit per day from all health and training sessions. 1 mark
ii. List all the points within the feasible region that result in this maximum profit. 1 mark
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
