QCAA Maths Methods Logarithmic Functions Mini Test 2
External Assessment Paper 2 — Technology-active
Number of marks: 7
Perusal time: 30 seconds
Writing time: 10 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Solve for \(x\) given that \(\log_3(x-1) = 2\).
- (A) 7
- (B) 8
- (C) 9
- (D) 10
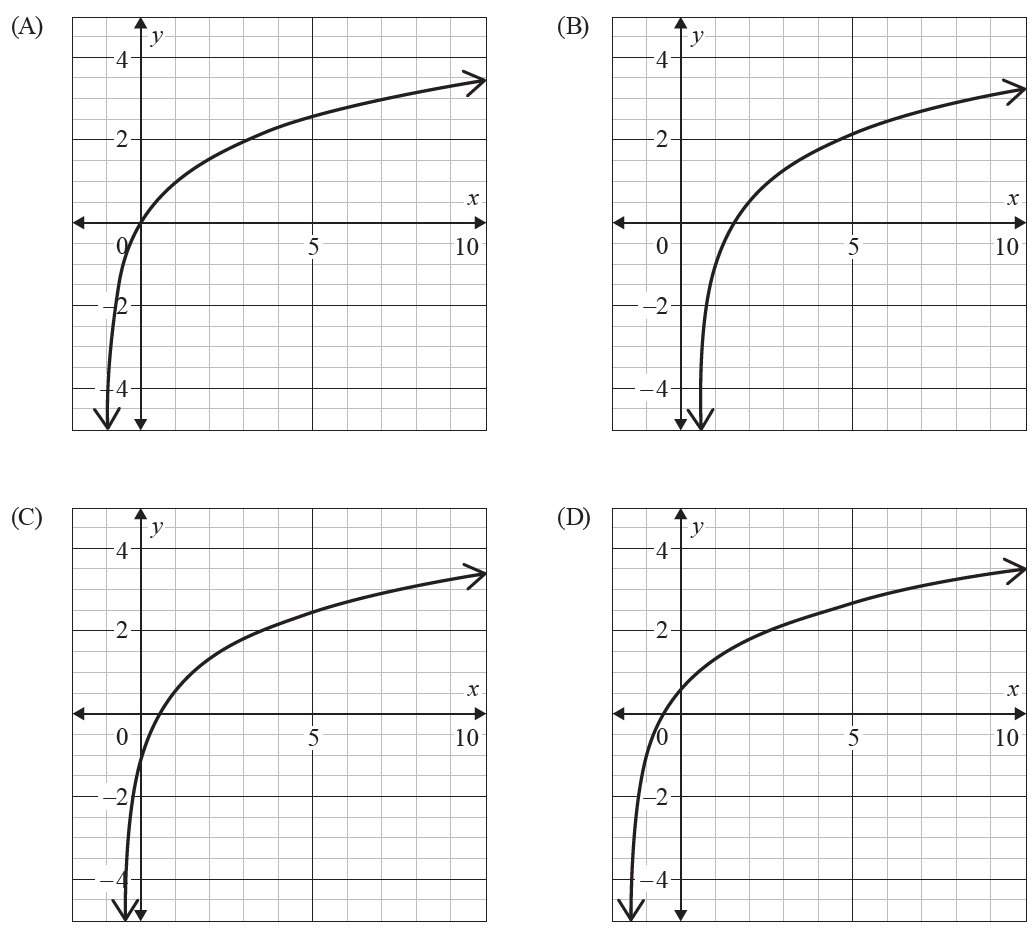
Consider the function \(f(x) = \log_p(x + q)\) where \(p > 1\) and \(0 < q < 1\).
Which of the following could be the graph of \(f(x)\)?
The pH of a substance is a measure of its acidity and is given by the formula pH = \(-\log_{10}[H^+]\) where \([H^+]\) is the concentration of hydrogen ions in moles per litre. If a solution has a pH equal to 0.2, the concentration of hydrogen ions in moles per litre is closest to
- (A) 0.32
- (B) 0.63
- (C) 0.70
- (D) 1.58
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A new internet search engine gives a ranking \(R\) to each website based on the function \( R = \log_{10}(50h^2) \), where \(h\) is the number of hits (visits) the website has received.
If a website currently has 100 hits, determine how many more hits they need to increase their ranking by 1.
END OF PAPER



