QCAA Maths Methods Differential Calculus Mini Test 1
External Assessment Paper 2 — Technology-active
Number of marks: 10
Perusal time: 1 minute
Writing time: 15 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
It is known that \(f'(x) = 0\) and \(f''(x) < 0\) for one of the labelled points on the graph of \(f(x)\).
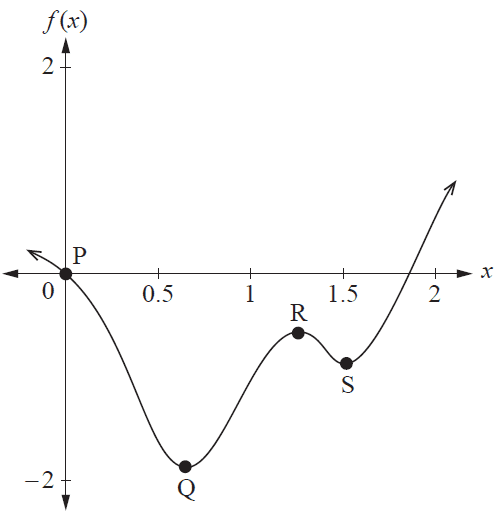
Which point matches this description?
- (A) \(P\)
- (B) \(Q\)
- (C) \(R\)
- (D) \(S\)
Determine the derivative of \(y = 2x \cos(3x)\).
- (A) \(2\cos(3x) - 6x \sin(3x)\)
- (B) \(2\cos(3x) + 6x \sin(3x)\)
- (C) \(-6\sin(3x)\)
- (D) \(-2\sin(3x)\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
The number of termites in a particular nest can be modelled by \(N(t) = \frac{A}{2+e^{-t}}\), where \(A\) is a constant and \(t\) represents time (months) since the nest first became a visible mound above ground level.
It is estimated that when the mound first became visible, the population was \(3 \times 10^5\) termites.
a) Determine the value of \(A\). [1 mark]
b) Determine the number of termites in the nest half a year after the mound became visible. [2 marks]
c) Determine the time in months after the mound became visible for the initial population to increase by 130 000 termites. Express the time as a decimal. [2 marks]
d) Develop a formula for the rate of change in the number of termites at any time after the mound became visible. Express your formula as a fraction. [2 marks]
e) Determine the rate of change in the number of termites five months after the mound became visible. [1 mark]
END OF PAPER



