QCAA Continuous Random Variables Mini Test 1
External Assessment Paper 1 — Technology-free
Number of marks: 12
Perusal time: 1 minute
Writing time: 18 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
The continuous random variable \(Y\) has the probability density function
\[ f(y) = \begin{cases} 1+y, & 0 \le y \le \sqrt{3}-1 \\ 0, & \text{otherwise} \end{cases} \]Determine \(P(0 \le y \le \frac{1}{2})\).
- (A) \(\frac{1}{5}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{5}{8}\)
- (D) \(\frac{3}{4}\)
Determine the mean of the continuous random variable \(X\) with the probability density function
\[ f(x) = \begin{cases} \frac{1}{8}x, & 0 \le x \le 4 \\ 0, & \text{otherwise} \end{cases} \]- (A) \(\frac{1}{8}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{1}{2}\)
- (D) \(\frac{8}{3}\)
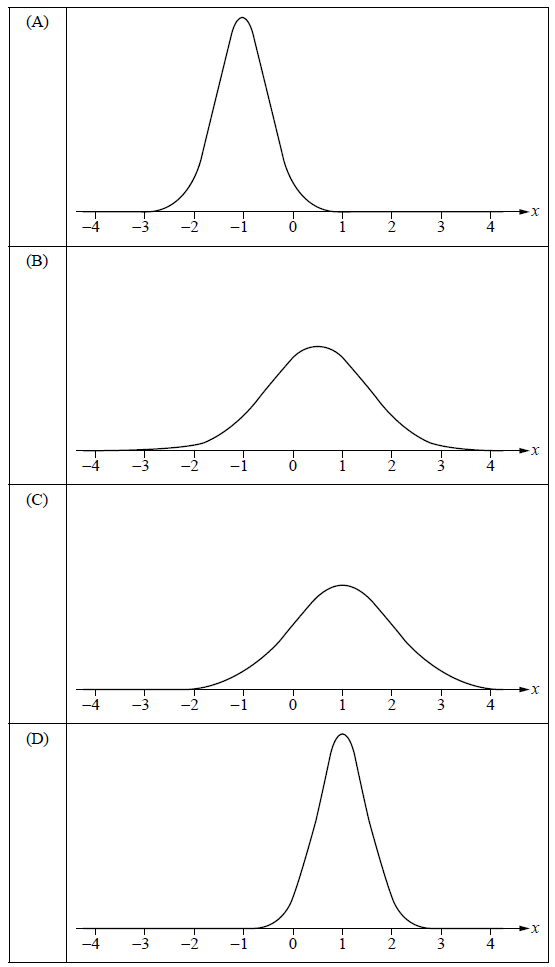
Which normal distribution curve best represents a normal distribution with a mean of 1 and a standard deviation of 0.5?
The weekly amount of money a company spends on repairs is normally distributed, with a mean of $1200 and a standard deviation of $100.
Given that \(\Pr(Z \le -2.5) = 0.0062\) and \(\Pr(Z > 1) = 0.1587\), where \(Z\) is a standard normal random variable, determine the probability that the weekly repair costs will be between $950 and $1300.
- (A) 0.6525
- (B) 0.6587
- (C) 0.8351
- (D) 0.8413
The continuous random variable \(X\) has the probability density function
\[ f(x) = \begin{cases} \frac{3}{x^2}, & 1 \le x \le \frac{3}{2} \\ 0, & \text{otherwise} \end{cases} \]The mean of \(X\) is
- (A) \(\ln\left(\frac{3}{2}\right)\)
- (B) \(\ln\left(\frac{27}{8}\right)\)
- (C) \(\ln\left(\frac{9}{2}\right)\)
- (D) 1
Pulse rates of adult men are approximately normally distributed with a mean of 70 and a standard deviation of 8. Which of the following choices correctly describes how to determine the proportion of men that have a pulse rate greater than 78?
- (A) Determine the area to the left of \(z = 1\) under the standard normal curve.
- (B) Determine the area to the right of \(z = 1\) under the standard normal curve.
- (C) Determine the area to the right of \(z = -1\) under the standard normal curve.
- (D) Determine the area between \(z = -1\) and \(z = 1\) under the standard normal curve.
The life expectancy (in years) of an electronic component can be represented by the probability density function
\[ p(x) = \begin{cases} \frac{1}{x^2}, & x \ge 1 \\ 0, & \text{otherwise} \end{cases} \]The probability that the component lasts between 1 and 10 years is
- (A) 0.010
- (B) 0.100
- (C) 0.900
- (D) 0.990
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A percentile is a measure in statistics showing the value below which a given percentage of observations occur.
The continuous random variable \(X\) has the probability density function
\[ f(x) = \begin{cases} 2x-2, & 1 \le x \le 2 \\ 0, & \text{otherwise} \end{cases} \]Determine the 36th percentile of \(X\).
END OF PAPER



