2024 QCE Maths Methods Paper 2 Mini Test 6
External Assessment Paper 2 — Technology-active
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Calculate the total enclosed area between the graph of \(y=x^2-x-6\) and the \(x\)-axis from \(x=1\) to \(x=5\).
- (A) 5.33
- (B) 7.33
- (C) 12.67
- (D) 20.00
It is known that \(f'(x) = 0\) and \(f''(x) < 0\) for one of the labelled points on the graph of \(f(x)\).
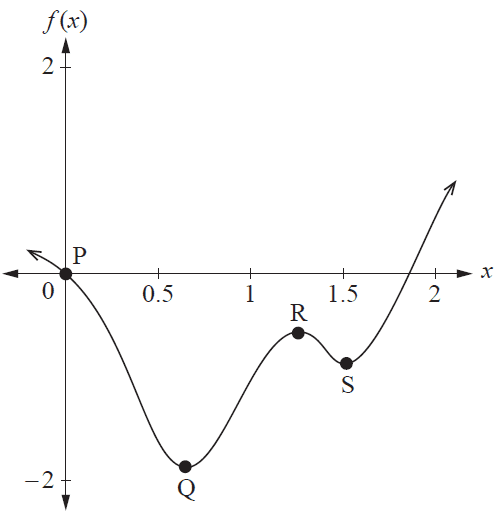
Which point matches this description?
- (A) \(P\)
- (B) \(Q\)
- (C) \(R\)
- (D) \(S\)
The velocity (m s\(^{-1}\)) at time \(t\) (s) of an object is given by \(v(t) = 0.4t^2 + 3t\) for \(t \ge 0\). The change in displacement (m) of the object from four to five seconds is
- (A) 15.43
- (B) 21.63
- (C) 32.53
- (D) 54.17
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
The normal distribution probability density function is \[ p(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \] with the parameters mean, \(\mu\), and standard deviation, \(\sigma\).
The speeds of electric scooter (e-scooter) riders on a particular section of a bike path are approximately normally distributed with a mean of 18 km/h. It is known that \(p(10) = 0.0135\).
The speed limit for e-scooters on this section of bike path is 23 km/h.
A speed camera is set up and records the speeds of 75 e-scooter riders. Every rider travelling faster than the speed limit is given a $143 fine. Before setting up the speed camera, the following suggestion was made.
Evaluate the reasonableness of this suggestion.
END OF PAPER



