2024 QCE Maths Methods Paper 2 Mini Test 5
External Assessment Paper 1 — Technology-free
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
The graph is of the form \(y = \log_a (x + b)\). A point on the graph \((4, 3)\) is labelled. The line \(x = -4\) is an asymptote.
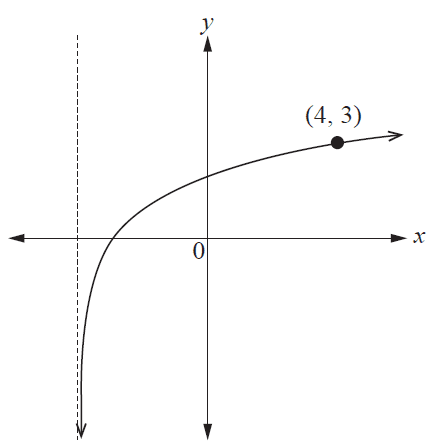
There is a point \(P(x_p, y_p)\) on the graph where \(y_p\) is twice the value of the \(y\)-intercept of the curve. Determine the value of \(x_p\).
The diagram shows some dimensions of a large storage container that is a rectangular prism. The angle \(\angle ABC\) is \(60^\circ\).
A person requires a container that is at least 4 metres in height.
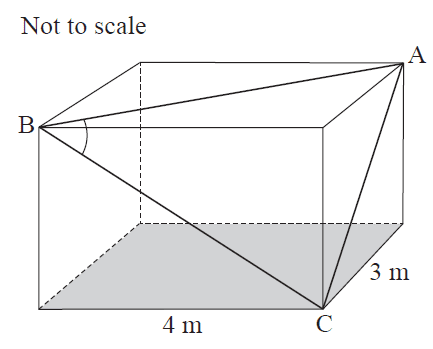
Make a justified decision about whether this storage container meets the person’s requirements.
END OF PAPER



