2024 QCE Maths Methods Paper 1 Mini Test 2
External Assessment Paper 1 — Technology-free
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Simplify \(y = 2\ln(e^x)\)
- (A) \(y = 2x\)
- (B) \(y = 2^x\)
- (C) \(y = \frac{2}{x}\)
- (D) \(y = x^2\)
Determine \(\int_a^b 2\cos(x)dx\), where \(a = \frac{\pi}{3}\) and \(b = \frac{\pi}{2}\).
- (A) \(1 - \frac{\sqrt{3}}{2}\)
- (B) \(\frac{\sqrt{3}}{2} - 1\)
- (C) \(2 - \sqrt{3}\)
- (D) \(\sqrt{3} - 2\)
Differentiate \(y = \ln(x)\cos(x)\) with respect to \(x\).
- (A) \(\frac{\cos(x)}{x}\)
- (B) \(-\frac{\sin(x)}{x}\)
- (C) \(\frac{\cos(x)}{x} + \ln(x)\sin(x)\)
- (D) \(\frac{\cos(x)}{x} - \ln(x)\sin(x)\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Each day over a three-day long weekend, a family spins a pointer on a circular board to decide whether they will spend the day at the beach or bushwalking. The circular board consists of three equal sections.
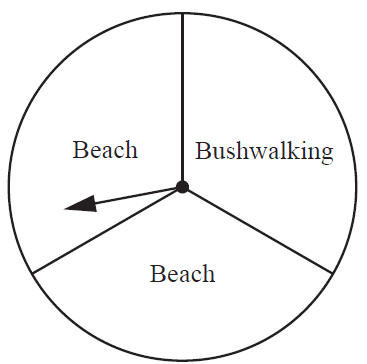
a) Determine the probability that the family will spend all three days bushwalking. [1 mark]
b) Determine the following binomial probabilities, expressed as fully simplified fractions.
i. Exactly two days will be spent at the beach. [2 marks]
ii. Fewer than three days will be spent at the beach. [3 marks]
END OF PAPER



