2023 QCAA Maths Methods External Exam Paper 1
Paper 1 — Technology-free
This is the full QCE Maths Methods External Exam with worked solutions. You can also try Mini-Tests, which are official QCAA exams split into short tests you can do anytime.
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
\(e^{\ln(x)}\) is equivalent to
- (A) \(0\)
- (B) \(1\)
- (C) \(x\)
- (D) \(\frac{1}{x}\)
If \(f(x) = e^{6-2x}\), determine the value of \(f'(2)\).
- (A) \(e^2\)
- (B) \(2e^2\)
- (C) \(-e^2\)
- (D) \(-2e^2\)
A bag contains 10 buttons of the same shape and size in different colours: 5 blue, 3 green and 2 red. If 3 buttons are randomly drawn from the bag, which probability can be calculated using the binomial distribution?
- (A) \(P(3 \text{ green})\) with replacement
- (B) \(P(3 \text{ blue})\) without replacement
- (C) \(P(2 \text{ green and } 1 \text{ red})\) with replacement
- (D) \(P(2 \text{ red and } 1 \text{ blue})\) without replacement
If the gradient of the function \(f(x)\) is given by \(\frac{20}{x^3}\), then \(f(x)\) is equal to
- (A) \(-\frac{60}{x^4} + c\)
- (B) \(-\frac{5}{x^4} + c\)
- (C) \(-\frac{10}{x^2} + c\)
- (D) \(-\frac{40}{x^2} + c\)
Determine \(\int_1^3 \frac{1}{2x} dx\).
- (A) \(\frac{1}{2} \ln 6\)
- (B) \(\frac{1}{2} \ln 5\)
- (C) \(\frac{1}{2} \ln 4\)
- (D) \(\frac{1}{2} \ln 3\)
Substitutions for \(h\) are used to estimate the limit of \(\frac{a^h - 1}{h}\) as \(h \to 0\). Which sequence is the most appropriate?
- (A) \(-4, -2, -1, -0.5, -0.25, -0.125 \dots\)
- (B) \(-0.05, -0.1, -0.2, -0.4, -0.8 \dots\)
- (C) \(2, 1, 0, -1, -2, -3 \dots\)
- (D) \(1, 2, 3, 4, 5, 6 \dots\)
Determine the mean of the continuous random variable \(X\) with the probability density function
\[ f(x) = \begin{cases} \frac{1}{8}x, & 0 \le x \le 4 \\ 0, & \text{otherwise} \end{cases} \]- (A) \(\frac{1}{8}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{1}{2}\)
- (D) \(\frac{8}{3}\)
A sample of size \(n\) was used to estimate a population proportion. An approximate margin of error of 3% was calculated using \(z = 1.96\). Given the sample proportion was 0.6, determine \(n\).
- (A) \(n = \frac{\left(\frac{0.03}{1.96}\right)^2}{0.24}\)
- (B) \(n = \frac{0.24}{\left(\frac{0.03}{1.96}\right)^2}\)
- (C) \(n = \frac{\left(\frac{0.03}{1.96}\right)^2}{2.4}\)
- (D) \(n = \frac{2.4}{\left(\frac{0.03}{1.96}\right)^2}\)
Determine \(\int_0^3 \pi \sin\left(\frac{\pi}{3}x\right)dx\).
- (A) \(3\)
- (B) \(6\)
- (C) \(-3\)
- (D) \(-6\)
The continuous random variable \(Y\) has the probability density function
\[ f(y) = \begin{cases} 1+y, & 0 \le y \le \sqrt{3}-1 \\ 0, & \text{otherwise} \end{cases} \]Determine \(P(0 \le y \le \frac{1}{2})\).
- (A) \(\frac{1}{5}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{5}{8}\)
- (D) \(\frac{3}{4}\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Two random samples (A and B) were obtained using two different Bernoulli experiments. Each Bernoulli trial in the random samples was recorded as 1 (for success) or 0 (for failure). The results are shown.
| A | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| B | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
In sample A, for each trial the mean is 0.8 and the variance is 0.16.
a) Use the sample B results to determine the mean and variance for each trial in sample B. [2 marks]
b) Compare the variability about the means of samples A and B. [2 marks]
The region bounded by the x-axis and the curve of \(f(x) = x(4-x)\) represents the plan of a garden bed. All measurements are in metres.
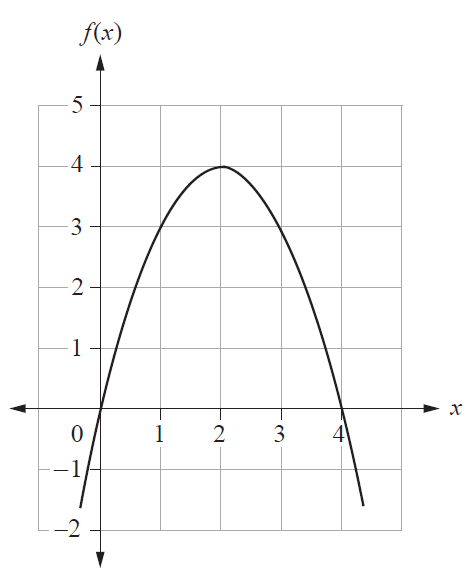
a) Estimate the area of the garden bed using sums of the form \(\sum_{i} f(x_i)\delta x_i\) where \(x_1 = 1\), \(x_2 = 2\), \(x_3 = 3\) and \(x_4 = 4\). [1 mark]
b) Use a definite integral to determine the area of the garden bed. [3 marks]
At a certain airport, the departure of one in five international flights is delayed every day. The status of any flight is independent of other flights.
One international flight is selected at random each day for three days. Each selection is recorded as either 'delayed' or 'not delayed'.
a) State two conditions that make this context suitable for modelling using a binomial random variable. [2 marks]
b) Calculate the probability that at least two of the selected flights were delayed. [3 marks]
The rate of change in the number of bacteria in a science experiment is represented by \(\frac{dP}{dt} = e^{2t}\), \(t \ge 0\), where \(t\) represents the time (hours) since starting the experiment and \(P\) represents the number of bacteria present (thousands). Initially there are 60 000 bacteria present, i.e. \(P(0) = 60\).
a) Determine the equation for \(P(t)\). [2 marks]
b) Determine the change in the number of bacteria during the third hour. Express your answer in terms of \(e\). [2 marks]
c) Determine how long it will take for the number of bacteria present to double after starting the experiment. [2 marks]
In a certain game, players throw one water balloon at a target. There is a one in four chance of hitting the target.
a) State the probabilities of all the possible outcomes for one throw at the target. [2 marks]
b) Let \(H\) be the discrete random variable for one of the possible outcomes. Determine the mean and variance of the distribution of random variable \(H\) when 20 players throw a water balloon at the target. [2 marks]
Solve for \(x\) in the equation \(4 + 7e^{-2x} = 3e^{2x}\).
A chemical is added to the water in a swimming pool at 10:00 am to prevent algae. The amount of chemical absorbed into the water over time \(t\) (hours) is represented by
\[A = 10t^2 - 4t^3, \quad 0 < t \le 1\frac{2}{3}\]Determine the time of day when the rate of absorption of the chemical is at its maximum. Use calculus techniques to verify that your time corresponds to a maximum rate.
A person enters the lowest carriage of a miniature Ferris wheel with a six-metre diameter. The bottom carriage is one metre off the ground. When top speed is reached, it takes three seconds for a carriage to travel from the lowest to the highest point of the ride. It is claimed that:
The vertical motion of the Ferris wheel produces a maximum vertical acceleration on each rider that is more than half the acceleration of free fall.
Free fall occurs when gravity is the only force acting, resulting in an acceleration of 9.8 ms\(^{-2}\).
Evaluate the reasonableness of the claim.
Jaxon and Shari each own a shop and have recorded the number of customers entering their shop on two consecutive days.
| Day 1 | Day 2 | |
| Jaxon's customers | 40 | 30 |
| Shari's customers | 10 | 20 |
| Total | 50 | 50 |
The number of daily customers for each shop can be modelled by the equation \(y = A \ln(Bx)\), where \(x\) is the day and \(y\) is the number of customers. The constants \(A\) and \(B\) are different for each shop.
Determine algebraically whether the total number of customers for Jaxon and Shari's shops will be the same every day in the future.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/


