QCAA Maths Methods 2022 Exam 2 with solutions
Number of marks: 8
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
The position (in cm) of a particle is given by \(x = \cos(4t)\), where \(t\) is time (in seconds). The velocity of the particle when \(t = 5\) is
- (A) 1.6323 cm s\(^{-1}\)
- (B) 0.4081 cm s\(^{-1}\)
- (C) –0.9129 cm s\(^{-1}\)
- (D) –3.6518 cm s\(^{-1}\)
Identify the correct features of the function \(f(x) = xe^x\)
- (A) \(f'(-1) = 0, f''(-1) < 0\)
- (B) \(f'(-1) = 0, f''(-1) > 0\)
- (C) \(f'(-1) < 0, f''(-1) < 0\)
- (D) \(f'(-1) < 0, f''(-1) > 0\)
The derivative of the function \(f(x)\) is given by \(f'(x) = \sin(x^3)\) for the domain \(-1.8 < x < 1.8\). The number of points of inflection that the graph of \(f(x)\) has on this interval is
- (A) 1
- (B) 3
- (C) 4
- (D) 5
The distribution for a sample proportion \(\hat{p}\) has a mean of 0.15 and a standard deviation of 0.0345. The sample size is
- (A) 10
- (B) 14
- (C) 107
- (D) 116
The continuous random variable \(X\) has the probability density function
\[ f(x) = \begin{cases} \frac{\cos(x)}{2}, & -\frac{\pi}{2} \le x \le \frac{\pi}{2} \\ 0, & \text{otherwise} \end{cases} \]The standard deviation of \(X\) is
- (A) 0.467
- (B) 0.684
- (C) 1.211
- (D) 1.467
A stall at the school fete sells cups of lemonade. Assuming the amount of lemonade in a cup is normally distributed with a mean of 60 mL and a standard deviation of 3 mL, 80% of the cups contain more than
- (A) 52.4 mL
- (B) 57.5 mL
- (C) 61.6 mL
- (D) 62.5 mL
A marble moves in one direction in a straight line with velocity \(v = 2\ln(t+1)\) (in metres per second) where \(t\) is time (in seconds) since the marble passed through the origin. Determine the distance from the origin the marble has rolled after 4 seconds.
- (A) 0.40 m
- (B) 1.60 m
- (C) 3.22 m
- (D) 8.09 m
Determine the equation of the asymptote of the function \(f(x) = \log_9(x-3) - 4\).
- (A) \(x = -4\)
- (B) \(x = -3\)
- (C) \(x = 3\)
- (D) \(x = 4\)
Determine the length of side AB in triangle ABC.
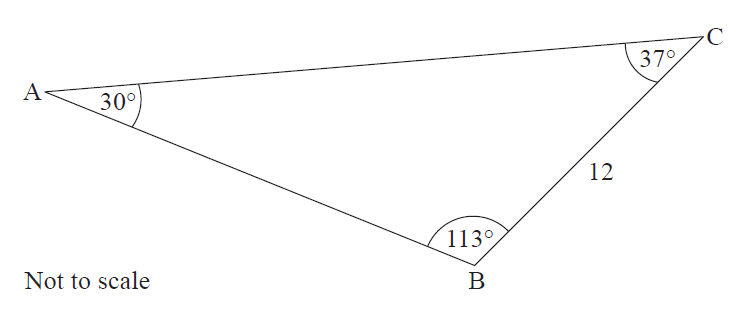
- (A) 22.13
- (B) 14.44
- (C) 9.97
- (D) 7.82
The solution of \(e^{2x-3} = 42\) is
- (A) 1.48
- (B) 2.31
- (C) 3.37
- (D) 4.54
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A salesperson has a 20% probability of making a sale to each customer who enters the store. Each sale is independent of all other sales.
a) Determine the mean number of sales on a day where 25 customers enter the store. [2 marks]
b) Determine the standard deviation of the number of sales on a day where 25 customers enter the store. [2 marks]
c) Determine the minimum number of customers who would have to enter the store to have an 88% chance or more of making at least one sale. [3 marks]
Suppose that the distance travelled by vehicles in a year can be modelled by a normal distribution. In 2021, vehicles travelled a mean of 13 700 km with a standard deviation of 3400 km.
a) Determine the probability that a vehicle chosen at random travelled less than 12 000 km in 2021. [2 marks]
b) Determine the value of \(x\) where 60% of vehicles travelled less than \(x\) km in 2021. [2 marks]
A sandy beach has a fence on one side and ocean on the other. The width of the beach is the distance (in metres) from the fence to the water's edge. The width, \(w(t)\), at a certain point is given by \[ w(t) = a + b \sin\left(\frac{\pi}{6}t - \frac{\pi}{3}\right), \quad 0 \le t \le 24 \]
where \(t\) is time (in hours) since 6 am. The width of the beach is 8 metres at 8 am and 3 metres at 5 pm.
a) Determine \(a\) and \(b\). [2 marks]
b) Determine the rate of change of the width of the beach at 8 am and the first time after this when this rate of change is repeated. [2 marks]
Ravi randomly sampled 200 different pet owners in Brisbane and found that 50 celebrate their pet's birthday.
a) Determine an approximate 95% confidence interval for the proportion of Brisbane pet owners who celebrate their pet's birthday. [2 marks]
Two of Ravi's friends also randomly sampled Brisbane pet owners. The results are shown in the table.
| Friend's name | Number sampled | Number who celebrate their pet's birthday |
| Khadija | 100 | 26 |
| Tim | 150 | 34 |
Khadija suggested a more precise estimate for the proportion of Brisbane pet owners who celebrate their pet's birthday could be obtained by combining their results.
b) Using all available data, determine an approximate 95% confidence interval for the proportion of Brisbane pet owners who celebrate their pet's birthday. [2 marks]
c) Use the results from Questions 14a) and 14b) to evaluate the reasonableness of Khadija's suggestion. [2 marks]
The proportion of all Brisbane pet owners who celebrate their pet's birthday is 0.24.
d) Using the normal approximation, determine the probability that in a randomly selected sample of size 200, more than 30% of pet owners celebrate their pet's birthday. [2 marks]
A hiker begins her journey at a youth hostel (\(H\)) and walks for 8 km on a bearing of 052°T to her lunch stop (\(L\)). She then walks on a bearing of 210°T for 5.2 km until she reaches a campsite (\(C\)).
Determine the direction she would need to walk in a straight line to return directly to the youth hostel.
The time spent waiting in a queue at a certain supermarket is given by (\(X + 11\)) minutes, where \(X\) is a random variable with the probability density function \[ f(x) = \begin{cases} \frac{a(4-x^2)}{32}, & -2 \le x \le 2 \\ 0, & \text{otherwise} \end{cases} \]
Determine the probability of waiting between 10 and 12 minutes in a queue at this supermarket.
A snail is travelling along a straight path from point \(A\). The snail's velocity (cm min\(^{-1}\)) is modelled by \(v(t) = 1.4 \ln(1 + t^2)\), where \(t\) is time (in minutes) for \(0 \le t \le 15\).
An ant passes point \(A\) 12 minutes after the snail and follows the snail's path. The ant moves with a constant acceleration of 2 cm min\(^{-2}\) and passes the snail at \(t = 15\) minutes.
Determine the ant's velocity at point \(A\).
The intelligence quotient (IQ) of individuals in a population is normally distributed, with a mean of 100 and a standard deviation of 16.
Nine individuals are chosen at random from the population.
Determine the probability that no more than two of the individuals have an IQ of at least 120.
Flying foxes enter and leave a fruit-growing region every evening. The rate at which the flying foxes enter the region is modelled by the function \[ A(t) = 42 \sin\left(0.03t - \frac{\pi}{3}\right) + 71, \quad 0 \le t \le 240 \]
The rate at which the flying foxes leave the region is modelled by the function \[ L(t) = 42 \sin\left(0.04t - \frac{\pi}{3}\right) + 42, \quad 0 \le t \le 240 \]
Both \(A(t)\) and \(L(t)\) are measured in animals per minute and \(t\) is measured in minutes after 7 pm.
There are 100 flying foxes in the region at 7 pm.
Determine the maximum number of flying foxes in the region and the time that this occurs.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/


