2021 QCE Maths Methods Paper 2 Mini Test 5
External Assessment Paper 2 — Technology-active
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Determine \(f(x)\), given \(f'(x) = 6x^2 + \frac{1}{x^2} + \frac{1}{x}\) and \(f(1) = 5\).
- (A) \(f(x) = 2x^3 + \frac{3}{x^3} + \ln(x) - 1\)
- (B) \(f(x) = 2x^3 - \frac{1}{x} + \ln(x) + 4\)
- (C) \(f(x) = 2x^3 - \frac{1}{x} + \frac{2}{x^2} + 2\)
- (D) \(f(x) = 2x^3 + \frac{3}{x^3} + \frac{2}{x^2} - 2\)
The displacement (in metres) of a particle is given by \(s(t) = -3\cos(t) + 2\sin(t)\), where \(t\) is in seconds.
The instantaneous velocity of the particle at time \(t = \frac{\pi}{2}\) seconds is
- (A) -3 m s\(^{-1}\)
- (B) -2 m s\(^{-1}\)
- (C) 2 m s\(^{-1}\)
- (D) 3 m s\(^{-1}\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Rabbits and foxes are among two species of mammals that live on an isolated island.
Rabbits represent a significant food source for the foxes.
The populations of rabbits and foxes were monitored each month for two years.
The graph shows the population of foxes (in thousands) and the population of rabbits (in thousands), at any time \(t\) (in months) over the two years. The two populations can be modelled using trigonometric functions.
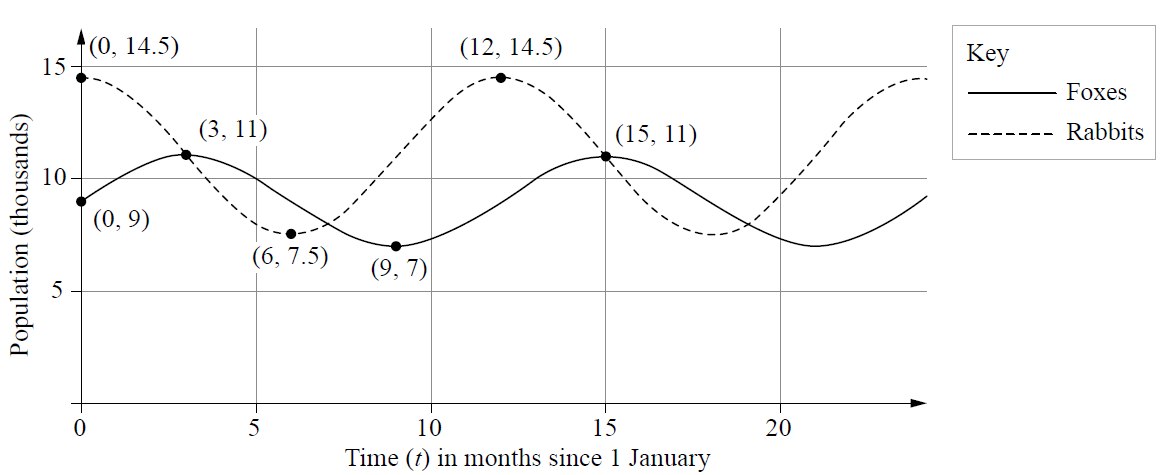
Jane believes that there were periods of time over the two years when the total population of foxes and rabbits on the island exceeded 25 000.
Evaluate the reasonableness of Jane's claim.
The number of animals in a population (in thousands) is modelled by the function \(P\) such that \[ P(t) = \frac{100}{1+4e^{-t}} \] where \(t\) is in years.
Determine the number of animals in the population when the population is growing the fastest.
END OF PAPER


