QCAA Maths Methods 2021 Exam 1 with solutions

Number of marks: 55

Perusal time: 5 minutes

Writing time: 90 minutes

Section 1

Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.

QUESTION 1 [2021 Paper 1 Q1]

\(2\log_{10}(x) - \log_{10}(3x)\) is equal to

(A) \(\log_{10}\left(\frac{x}{3}\right)\)
(B) \(\log_{10}(x^2 - 3x)\)
(C) \(\frac{2\log_{10}(x)}{\log_{10}(3x)}\)
(D) \(-\log_{10}(x)\)

QUESTION 2 [2021 Paper 1 Q2]

The table shows the time a technician has spent servicing photocopiers.

Time (in minutes)	Frequency
\(0 \le t < 5\)	10
\(5 \le t < 10\)	20
\(10 \le t < 15\)	30
\(15 \le t < 20\)	40

What is the probability that a given service required at least 10 minutes but less than 20 minutes?

(A) 0.15
(B) 0.35
(C) 0.70
(D) 0.85

QUESTION 3 [2021 Paper 1 Q3]

Determine \(\int 10e^{4x} dx\)

(A) \(\frac{10e^{4x+1}}{4x+1} + c\)
(B) \(40e^{4x} + c\)
(C) \(\frac{5}{2}e^{4x} + c\)
(D) \(2e^{5x} + c\)

QUESTION 4 [2021 Paper 1 Q4]

The second derivative of the function \(f(x)\) is given by \(f''(x) = \frac{2x}{1+x^2}\).
The interval on which the graph of \(f(x)\) is concave up is

(A) \(x < 0\)
(B) \(x \le 0\)
(C) \(x > 0\)
(D) \(x \ge 0\)

QUESTION 5 [2021 Paper 1 Q5]

The graph of \(f''(x)\) is shown.

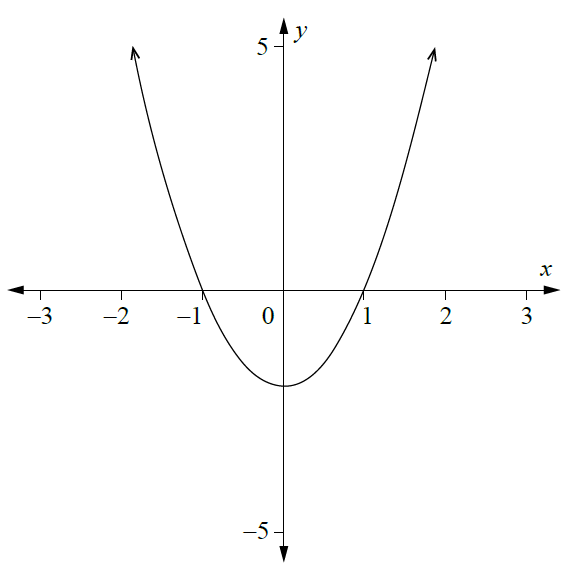
Graph of the second derivative, f''(x), which is a parabola opening upwards with its vertex at (0, -2) and x-intercepts at approximately -1.4 and 1.4.

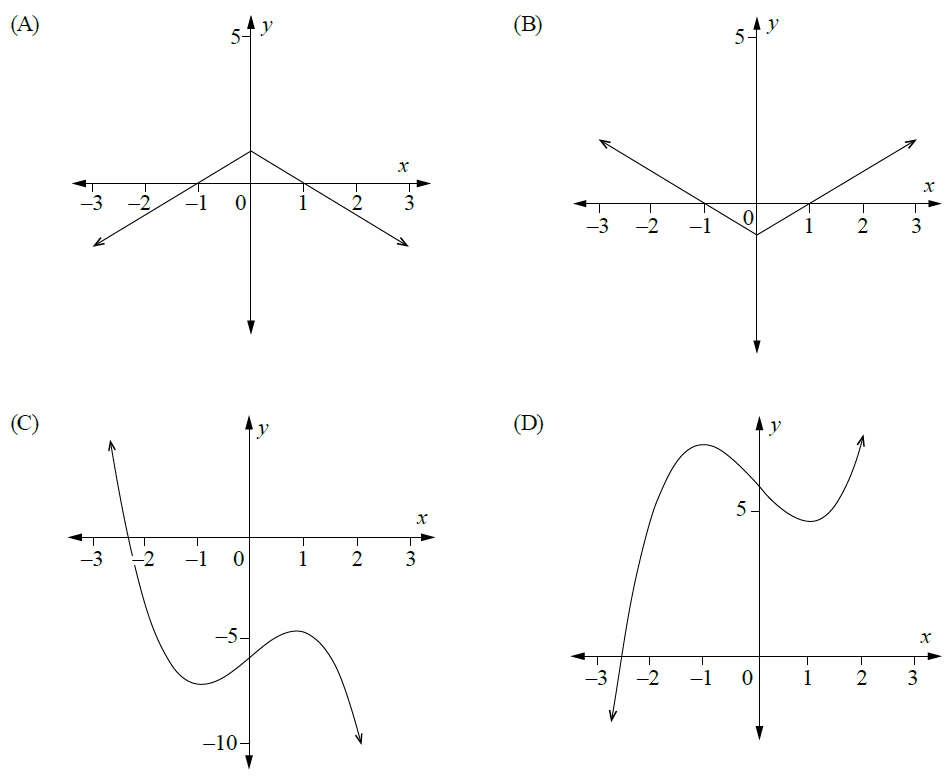
Which of the following could be the graph of \(f'(x)\)?

Graph for option A, showing a V-shape function with vertex at (0, 2).

QUESTION 6 [2021 Paper 1 Q6]

A random variable \(X\) is the number of successes in a Bernoulli experiment with \(n\) trials, each with a probability of success \(p\) and a probability of failure \(q\). The probability distribution table of \(X\) is shown.

\(k\)	\(P(X=k)\)
0	\(\frac{1}{81}\)
1	\(\frac{8}{81}\)
2	\(\frac{24}{81}\)
3	\(\frac{32}{81}\)
4	\(\frac{16}{81}\)

Which values of \(n\), \(p\) and \(q\) will generate this probability distribution?

(A) \(n=4, p=\frac{2}{3}, q=\frac{1}{3}\)
(B) \(n=4, p=\frac{1}{3}, q=\frac{2}{3}\)
(C) \(n=5, p=\frac{2}{3}, q=\frac{1}{3}\)
(D) \(n=5, p=\frac{1}{3}, q=\frac{2}{3}\)

QUESTION 7 [2021 Paper 1 Q7]

Determine \(\int_{1}^{3} (2x+3)dx\)

(A) 2
(B) 4
(C) 14
(D) 16

QUESTION 8 [2021 Paper 1 Q8]

The continuous random variable \(X\) has the probability density function

\[ f(x) = \begin{cases} \frac{3}{x^2}, & 1 \le x \le \frac{3}{2} \\ 0, & \text{otherwise} \end{cases} \]

The mean of \(X\) is

(A) \(\ln\left(\frac{3}{2}\right)\)
(B) \(\ln\left(\frac{27}{8}\right)\)
(C) \(\ln\left(\frac{9}{2}\right)\)
(D) 1

QUESTION 9 [2021 Paper 1 Q9]

A basket contains 10 green apples and 30 red apples. Three apples are drawn at random from the basket with replacement. Determine the probability that exactly two of the three apples are green.

(A) \(\frac{3}{64}\)
(B) \(\frac{9}{64}\)
(C) \(\frac{10}{64}\)
(D) \(\frac{27}{64}\)

QUESTION 10 [2021 Paper 1 Q10]

Handspans of teenagers are approximately normally distributed, with a mean of 15 cm and a standard deviation of 2 cm.

Which of the following groups is expected to be the largest?

(A) teenagers with handspans that are between 7 cm and 11 cm
(B) teenagers with handspans that are between 11 cm and 15 cm
(C) teenagers with handspans that are between 13 cm and 17 cm
(D) teenagers with handspans that are between 17 cm and 21 cm

Section 2

Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.

QUESTION 11 (5 marks) [2021 Paper 1 Q11]

Determine the derivative with respect to \(x\) of the following functions.

a) \(y = (e^x + 1)^3\) [2 marks]

b) \(y = \frac{\sin(x)}{x^2}\) (Give your answer in simplest form.) [3 marks]

QUESTION 12 (5 marks) [2021 Paper 1 Q12]

Solve for \(x\) in the following.

a) \(\log_2(5x+7) = 5\) [2 marks]

b) \(\log_{10}(x+3) + \log_{10}(x-3) = \log_{10}(9x-29)\) [3 marks]

QUESTION 13 (5 marks) [2021 Paper 1 Q13]

Consider the functions \(f(x) = x^2\) and \(g(x) = 4x\).

a) Determine the \(x\)-coordinates of the points of intersection of the graphs of the two functions. [2 marks]

b) Use the results from Question 13a) to calculate the area enclosed by the graphs of \(f(x)\) and \(g(x)\). [3 marks]

QUESTION 14 (4 marks) [2021 Paper 1 Q14]

Consider the function \(f(x) = \ln(3x+4)\), for \(x > \frac{-4}{3}\).

a) Determine \(f'(x)\). [1 mark]

b) Determine the \(x\)-intercept of the graph of \(f(x)\). [2 marks]

c) Determine the gradient of the tangent to the graph of \(f(x)\) at the \(x\)-intercept. [1 mark]

QUESTION 15 (4 marks) [2021 Paper 1 Q15]

In the isosceles triangle \(ABC\), angle \(C\) is \(120^\circ\) and side \(a\) is 4 cm.

a) Draw the triangle, indicating all given information. [1 mark]

Note: If you make a mistake in the diagram, cancel it by ruling a single diagonal line through your work and use the additional diagram on page 17 of this question and response book.

b) Calculate the area of the triangle in cm\(^2\). (Give your answer in simplest form.) [3 marks]

QUESTION 16 (4 marks) [2021 Paper 1 Q16]

A tangent is drawn at the point \((1, e)\) on the graph of the function \(y = e^{2-x}\) as shown.

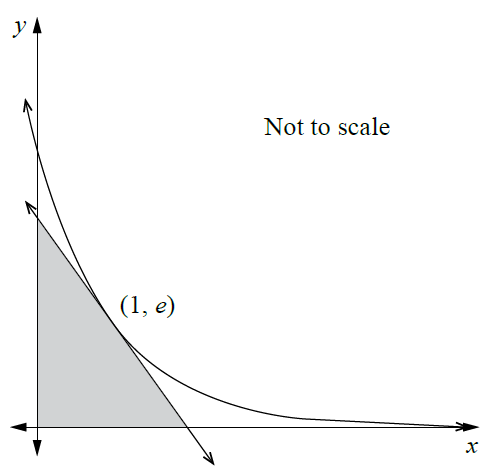
Graph of y = e^(2-x) with a tangent at (1, e)

Determine the area of the shaded triangle.

QUESTION 17 (3 marks) [2021 Paper 1 Q17]

In any five-day working week Leonardo either catches a bus to work or uses another form of transportation. On average, he catches the bus to work on three of the five days. His decision on any given day is independent of his decision on any other day.

Determine the probability that Leonardo catches a bus to work on exactly one day in a given five-day working week.

QUESTION 18 (4 marks) [2021 Paper 1 Q18]

The graph of \(y = f(x)\), where \(f(x)\) is the quadratic function \(f(x) = ax^2 + bx + 4\), is shown. Two regions of the area between the graph of \(y = f(x)\) and the \(x\)-axis are shaded.

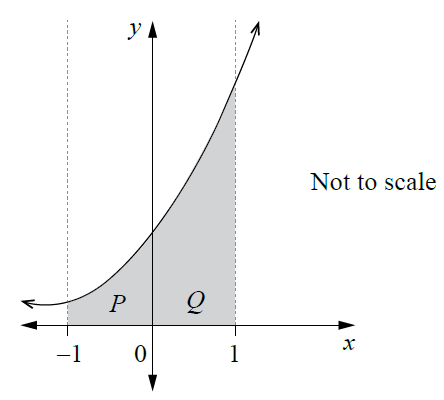
Graph of a quadratic function f(x) with shaded areas P and Q

Region \(P\) has an area of \(\frac{13}{6}\) units\(^2\) and Region \(Q\) has an area of \(\frac{43}{6}\) units\(^2\).

Determine the values of \(a\) and \(b\).

QUESTION 19 (4 marks) [2021 Paper 1 Q19]

A firm aims to have 95% confidence in estimating the proportion of office workers who respond to an email in less than an hour to within \(\pm 0.05\).

A survey has never been undertaken before, so no past data is available.

The firm believes that if the proportion is 0.5, then this will result in the largest variability in the sample proportion.

Based on this, determine the sample size needed using the approximate value of \(z = 2\) for the 95% confidence interval.

Justify the choice of 0.5 for the proportion.

QUESTION 20 (7 marks) [2021 Paper 1 Q20]

The population of rabbits (\(P\)) on an island, in hundreds, is given by \(P(t) = t^2 \ln(3t) + 6\), \(t > 0\), where \(t\) is time in years.

Determine the intervals of time when the population is increasing and the intervals when it is decreasing.

END OF PAPER

QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/