VCE General Maths Networks and Decision Mathematics 2017 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 2.5 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Networks and decision mathematics - 2017 - Exam 2
Bus routes connect six towns.
The towns are Northend (N), Opera (O), Palmer (P), Quigley (Q), Rosebush (R) and Seatown (S).
The graph below gives the cost, in dollars, of bus travel along these routes.
Bai lives in Northend (N) and he will travel by bus to take a holiday in Seatown (S).
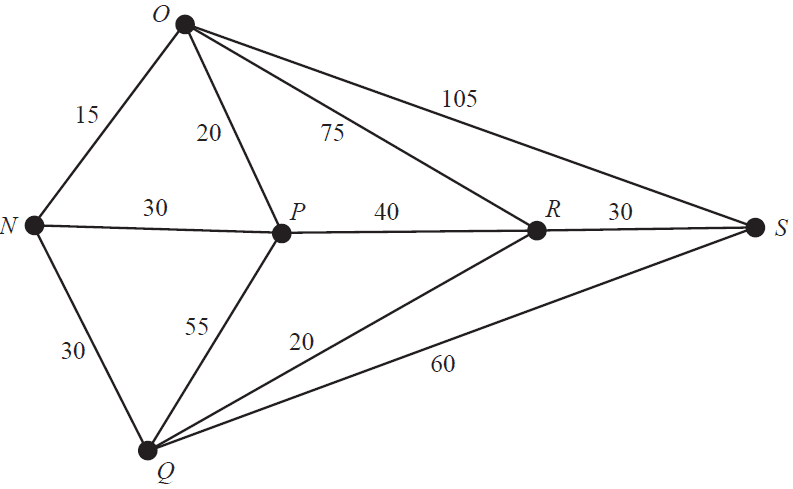
a. Bai considers travelling by bus along the route Northend (N) – Opera (O) – Seatown (S).
How much would Bai have to pay? 1 mark
b. If Bai takes the cheapest route from Northend (N) to Seatown (S), which other town(s) will he pass through? 1 mark
c. Euler's formula, \(v + f = e + 2\), holds for this graph.
Complete the formula by writing the appropriate numbers in the boxes provided below. 1 mark

Bai joins his friends Agatha, Colin and Diane when he arrives for the holiday in Seatown.
Each person will plan one tour that the group will take.
Table 1 shows the time, in minutes, it would take each person to plan each of the four tours.
Table 1
| Agatha | Bai | Colin | Diane | |
|---|---|---|---|---|
| Tour 1 | 13 | 7 | 13 | 12 |
| Tour 2 | 14 | 9 | 8 | 7 |
| Tour 3 | 19 | 25 | 21 | 18 |
| Tour 4 | 10 | 7 | 11 | 10 |
The aim is to minimise the total time it takes to plan the four tours.
Agatha applies the Hungarian algorithm to Table 1 to produce Table 2.
Table 2 shows the final result of all her steps of the Hungarian algorithm.
Table 2
| Agatha | Bai | Colin | Diane | |
|---|---|---|---|---|
| Tour 1 | 3 | 0 | 3 | 3 |
| Tour 2 | 6 | 4 | 0 | 0 |
| Tour 3 | 0 | 9 | 2 | 0 |
| Tour 4 | 0 | 0 | 1 | 1 |
a. In Table 2 there is a zero in the column for Colin.
When all values in the table are considered, what conclusion about minimum total planning time can be made from this zero? 1 mark
b. Determine the minimum total planning time, in minutes, for all four tours. 1 mark
While on holiday, the four friends visit a theme park where there are nine rides.
On the graph below, the positions of the rides are indicated by the vertices.
The numbers on the edges represent the distances, in metres, between rides.
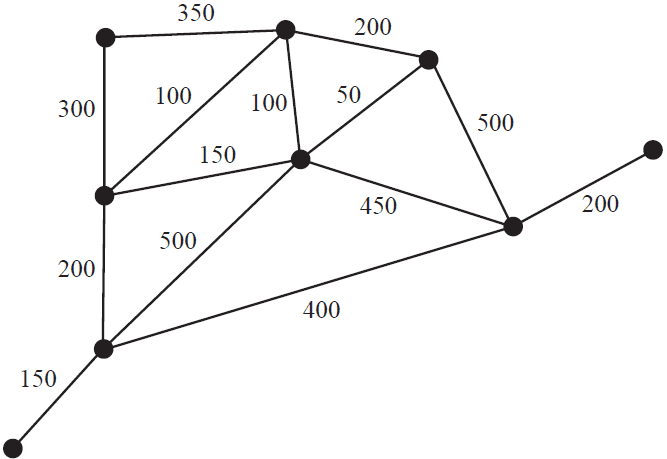
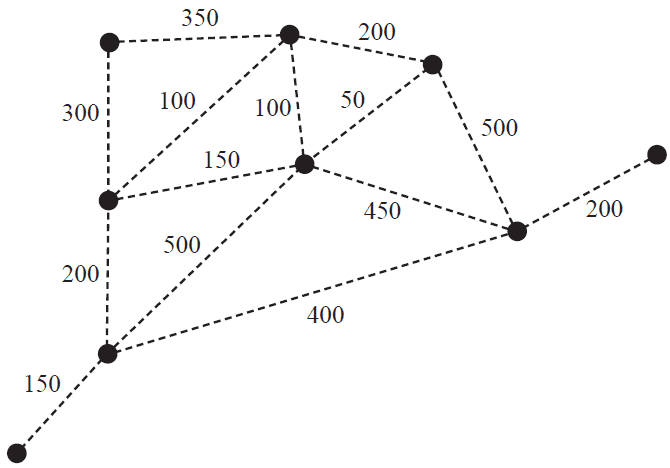
a. Electrical cables are required to power the rides.
These cables will form a connected graph.
The shortest total length of cable will be used.
i. Give a mathematical term to describe a graph that represents these cables. 1 mark
ii. Draw in the graph that represents these cables on the diagram below. 1 mark
The rides at the theme park are set up at the beginning of each holiday season.
This project involves activities A to O.
The directed network below shows these activities and their completion times in days.
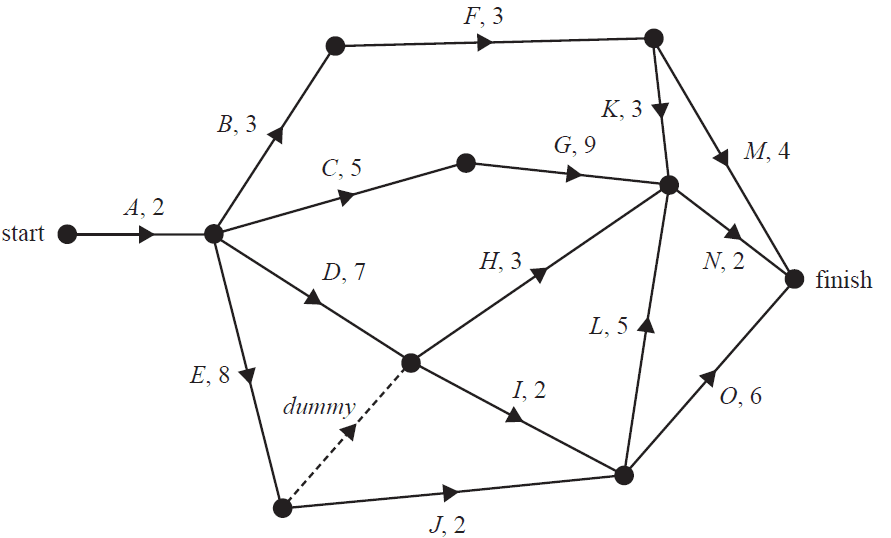
a. Write down the two immediate predecessors of activity I. 1 mark
b. The minimum completion time for the project is 19 days.
i. There are two critical paths. One of the critical paths is A–E–J–L–N.
Write down the other critical path. 1 mark
ii. Determine the float time, in days, for activity F. 1 mark
c. The project could finish earlier if some activities were crashed.
Six activities, B, D, G, I, J and L, can all be reduced by one day.
The cost of this crashing is $1000 per activity.
i. What is the minimum number of days in which the project could now be completed? 1 mark
ii. What is the minimum cost of completing the project in this time? 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
