VCE General Maths Networks and Decision Mathematics 2018 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Networks and decision mathematics - 2018 - Exam 2
The graph below shows the possible number of postal deliveries each day between the Central Mail Depot and the Zenith Post Office.
The unmarked vertices represent other depots in the region.
The weighting of each edge represents the maximum number of deliveries that can be made each day.
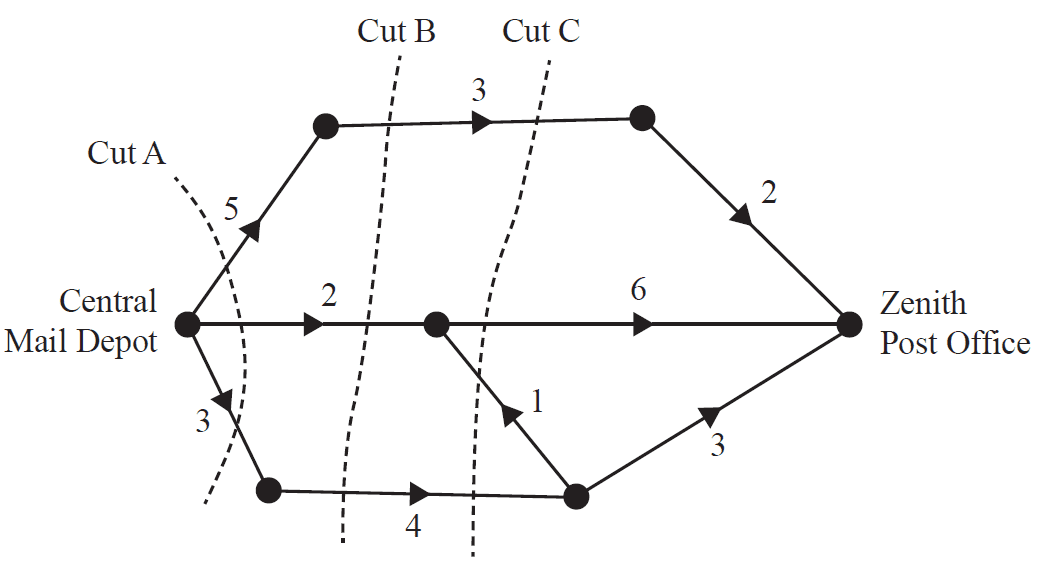
a. Cut A, shown on the graph, has a capacity of 10.
Two other cuts are labelled as Cut B and Cut C.
i. Write down the capacity of Cut B. 1 mark
ii. Write down the capacity of Cut C. 1 mark
b. Determine the maximum number of deliveries that can be made each day from the Central Mail Depot to the Zenith Post Office. 1 mark
In one area of the town of Zenith, a postal worker delivers mail to 10 houses labelled as vertices \(A\) to \(J\) on the graph below.
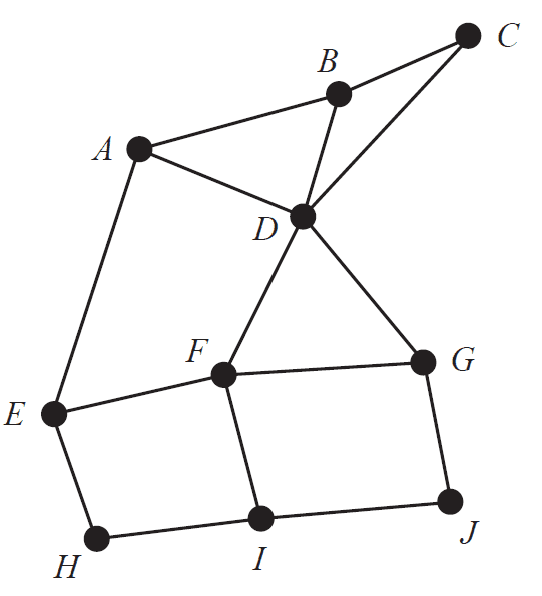
a. Which one of the vertices on the graph has degree 4? 1 mark
For this graph, an Eulerian trail does not currently exist.
b. For an Eulerian trail to exist, what is the minimum number of extra edges that the graph would require? 1 mark
c. The postal worker has delivered the mail at \(F\) and will continue her deliveries by following a Hamiltonian path from \(F\).
Draw in a possible Hamiltonian path for the postal worker on the diagram below. 1 mark
At the Zenith Post Office all computer systems are to be upgraded.
This project involves 10 activities, \(A\) to \(J\).
The directed network below shows these activities and their completion times, in hours.
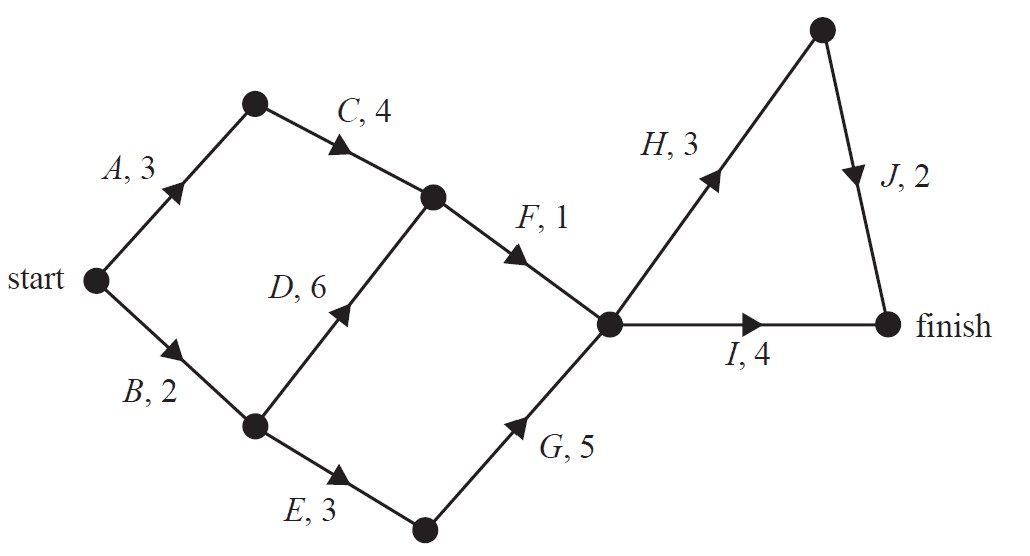
a. Determine the earliest starting time, in hours, for activity \(I\). 1 mark
b. The minimum completion time for the project is 15 hours.
Write down the critical path. 1 mark
c. Two of the activities have a float time of two hours.
Write down these two activities. 1 mark
d. For the next upgrade, the same project will be repeated but one extra activity will be added.
This activity has a duration of one hour, an earliest starting time of five hours and a latest starting time of 12 hours.
Complete the following sentence by filling in the boxes provided. 1 mark
The extra activity could be represented on the network above by a directed edge from the
end of activity to the start of activity .
Parcel deliveries are made between five nearby towns, \(P\) to \(T\).
The roads connecting these five towns are shown on the graph below. The distances, in kilometres, are also shown.
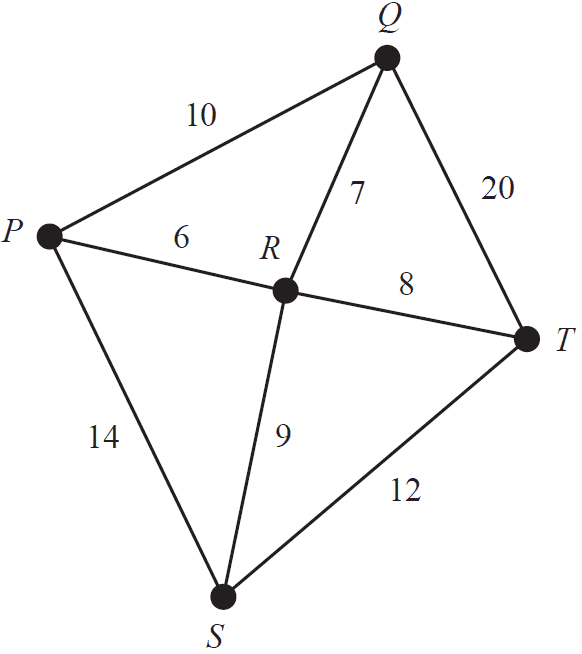
A road inspector will leave from town \(P\) to check all the roads and return to town \(P\) when the inspection is complete. He will travel the minimum distance possible.
a. How many roads will the inspector have to travel on more than once? 1 mark
b. Determine the minimum distance, in kilometres, that the inspector will travel. 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
