VCE General Maths Networks and Decision Mathematics 2024 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Networks and decision mathematics - 2024 - Exam 2 (Part 1)
A supermarket has five departments, with areas allocated as shown on the floorplan below.
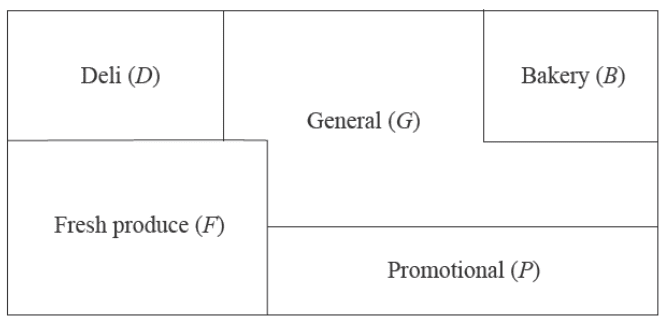
The floorplan is represented by the graph below.
On this graph, vertices represent departments and edges represent boundaries between two departments.
This graph is incomplete.
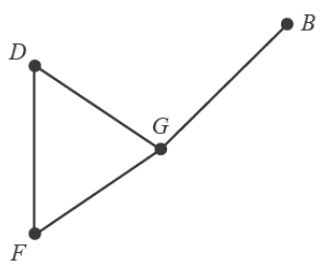
a. Draw the missing vertex and missing edges on the graph above. Include a label. 1 mark
Karla is standing in the Promotional department.
She wants to visit each department in the supermarket once only.
b.
i. In which department will she finish? 1 mark
ii. What is the mathematical name for this type of journey? 1 mark
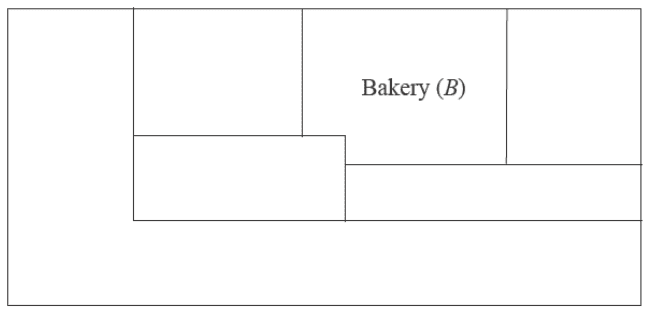
c. The supermarket adds a new Entertainment department (\(E\)), and the floorplan is rearranged.
The boundaries between the departments are represented in the adjacency matrix below, where a ‘1’ indicates a boundary between the departments.
\[ \begin{array}{@{}c@{\,}c} & \begin{array}{@{}cccccc@{}} B & D & E & F & G & P \end{array} \\ \begin{matrix} B \\ D \\ E \\ F \\ G \\ P \end{matrix} & \left[ \begin{array}{cccccc} 0 & 1 & 1 & 1 & 0 & 1 \\ 1 & 0 & 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 & 1 \\ 1 & 1 & 0 & 0 & 1 & 1 \\ 0 & 1 & 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 1 & 1 & 0 \end{array} \right] \end{array} \]
Use the adjacency matrix to complete the floorplan below by labelling each department. The Bakery (\(B\)) is already labelled. 1 mark
A manufacturer (\(M\)) makes deliveries to the supermarket (\(S\)) via a number of storage warehouses, \(L, N, O, P, Q\) and \(R\). These eight locations are represented as vertices in the network below.
The numbers on the edges represent the maximum number of deliveries that can be made between these locations each day.
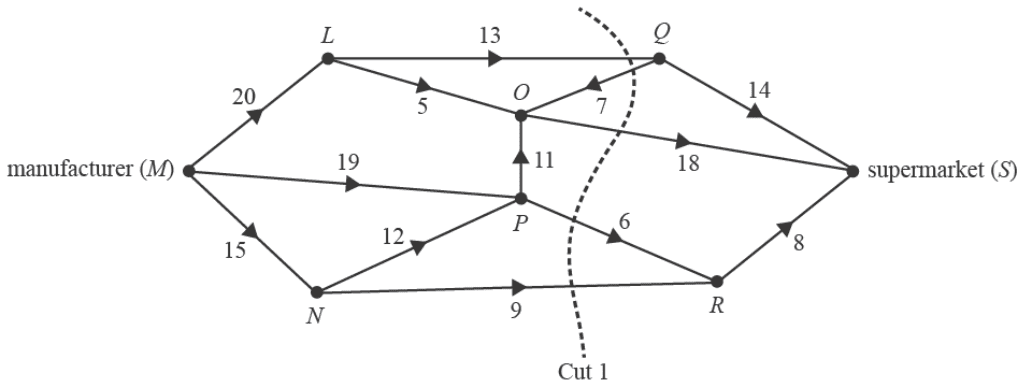
a. When considering the possible flow of deliveries through this network, many different cuts can be made.
Determine the capacity of Cut 1, shown above. 1 mark
b. Determine the maximum number of deliveries that can be made each day from the manufacturer to the supermarket. 1 mark
c. The manufacturer wants to increase the number of deliveries to the supermarket.
This can be achieved by increasing the number of deliveries between one pair of locations.
Complete the following sentence by writing the locations in the boxes provided:
To maximise this increase, the number of deliveries should be increased between locations and 1 mark
An upgrade to the supermarket requires the completion of 11 activities, \(A\) to \(K\).
The directed network below shows these activities and their completion time, in weeks.
The minimum completion time for the project is 29 weeks.
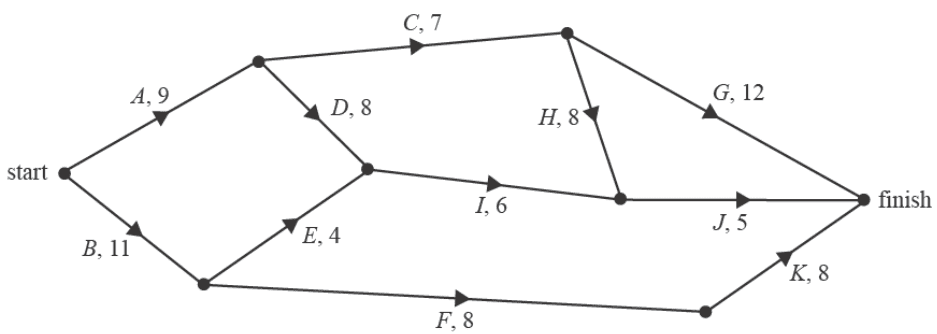
a. Write down the critical path. 1 mark
b. Which activity can be delayed for the longest time without affecting the minimum completion time of the project? 1 mark
Use the following information to answer parts c–e.
A change is made to the order of activities.
The table below shows the activities and their new latest starting times in weeks.
| Activity | Latest starting time (weeks) |
|---|---|
| A | 0 |
| B | 2 |
| C | 10 |
| D | 9 |
| E | 13 |
| F | 14 |
| G | 18 |
| H | 17 |
| I | 19 |
| J | 25 |
| K | 22 |
A dummy activity is now required in the network.
c. On the directed network below, draw a directed edge to represent the dummy activity. Include a label. 1 mark
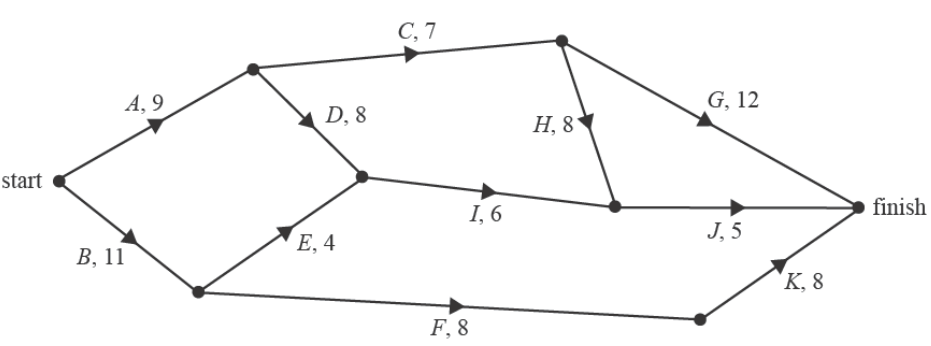
d. What is the new minimum completion time of the project? 1 mark
e. The owners of the supermarket want the project completed earlier.
They will pay to reduce the time of some of the activities.
A reduction in completion time of an activity will incur an additional cost of $10 000 per week.
Activities can be reduced by a maximum of two weeks.
The minimum number of weeks an activity can be reduced to is seven weeks.
What is the minimum amount the owners of the supermarket will have to pay to reduce the completion time of the project as much as possible? 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
