VCE General Maths Networks and Decision Mathematics 2016 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Networks and decision mathematics - 2016
Lee, Mandy, Nola, Oscar and Pieter are each to be allocated one particular task at work.
The bipartite graph below shows which task(s), 1–5, each person is able to complete.
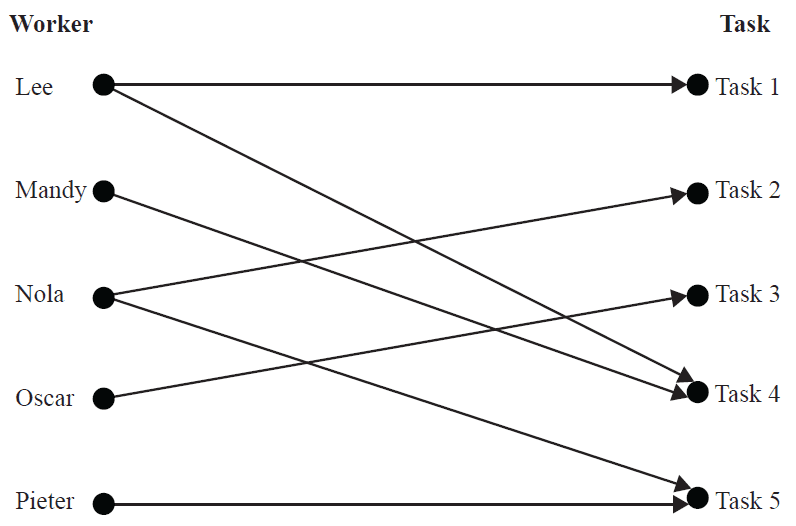
Each person completes a different task.
Task 4 must be completed by
- A. Lee.
- B. Mandy.
- C. Nola.
- D. Oscar.
- E. Pieter.
The following directed graph shows the flow of water, in litres per minute, in a system of pipes connecting the source to the sink.
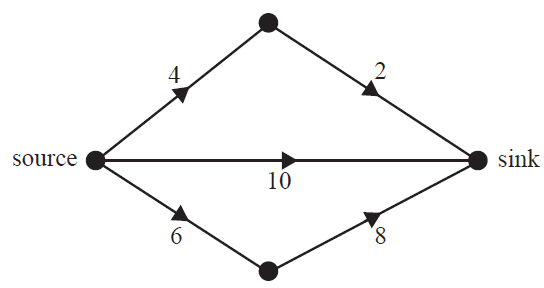
The maximum flow, in litres per minute, from the source to the sink is
- A. 10
- B. 14
- C. 18
- D. 20
- E. 22
The following graph with five vertices is a complete graph.
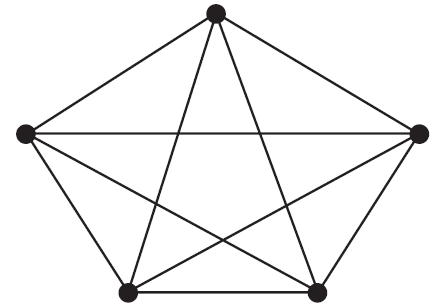
Edges are removed so that the graph will have the minimum number of edges to remain connected.
The number of edges that are removed is
- A. 4
- B. 5
- C. 6
- D. 9
- E. 10
The minimum spanning tree for the network below includes the edge with weight labelled \(k\).
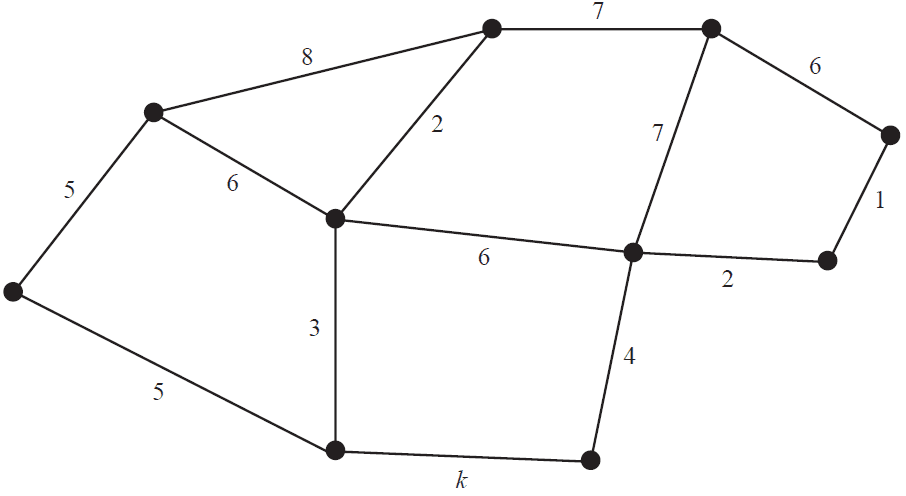
The total weight of all edges for the minimum spanning tree is 33.
The value of \(k\) is
- A. 1
- B. 2
- C. 3
- D. 4
- E. 5
Consider the planar graph below.
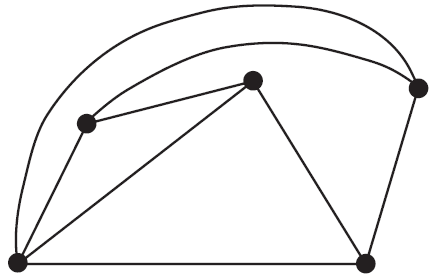
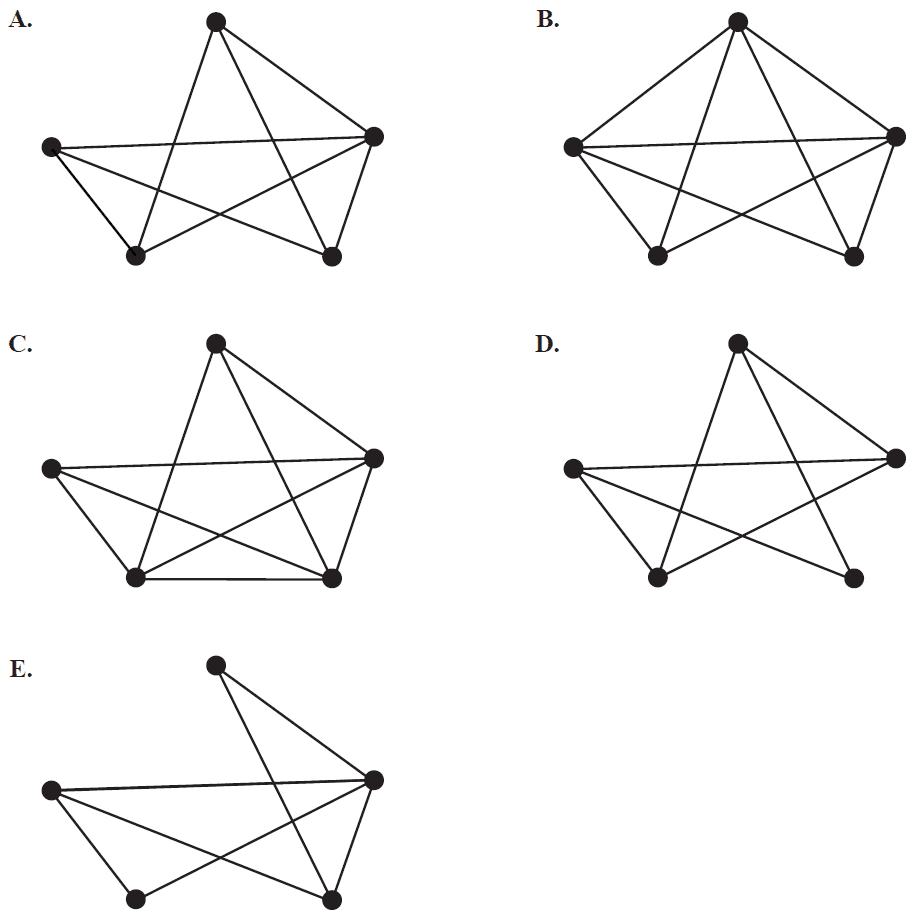
Which one of the following graphs can be redrawn as the planar graph above?
Use the following information to answer Questions 6 and 7.
The directed graph below shows the sequence of activities required to complete a project.
All times are in hours.
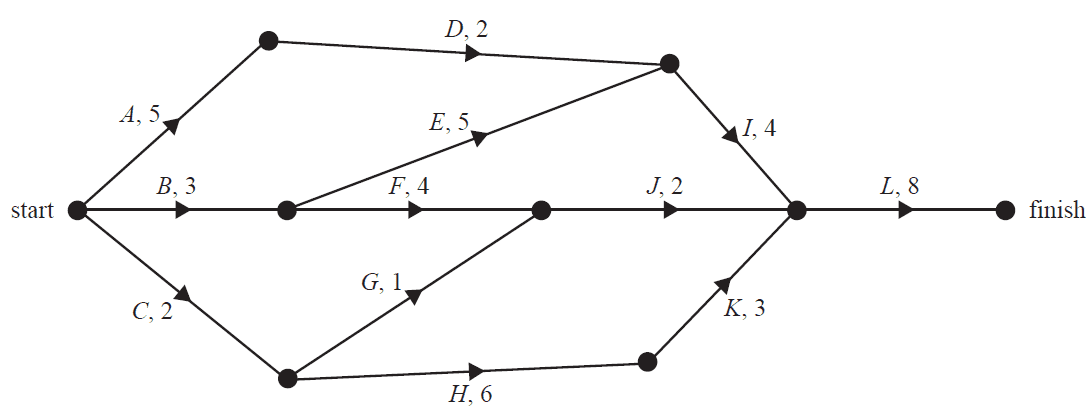
The number of activities that have exactly two immediate predecessors is
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
There is one critical path for this project.
Three critical paths would exist if the duration of activity
- A. \(I\) were reduced by two hours.
- B. \(E\) were reduced by one hour.
- C. \(G\) were increased by six hours.
- D. \(K\) were increased by two hours.
- E. \(F\) were increased by two hours.
Five children, Alan, Brianna, Chamath, Deidre and Ewen, are each to be assigned a different job by their teacher. The table below shows the time, in minutes, that each child would take to complete each of the five jobs.
| Alan | Brianna | Chamath | Deidre | Ewen | |
|---|---|---|---|---|---|
| Job 1 | 5 | 8 | 5 | 8 | 7 |
| Job 2 | 5 | 7 | 6 | 7 | 4 |
| Job 3 | 9 | 5 | 7 | 5 | 9 |
| Job 4 | 7 | 7 | 9 | 8 | 5 |
| Job 5 | 4 | 4 | 4 | 4 | 3 |
The teacher wants to allocate the jobs so as to minimise the total time taken to complete the five jobs.
In doing so, she finds that two allocations are possible.
If each child starts their allocated job at the same time, then the first child to finish could be either
- A. Alan or Brianna.
- B. Brianna or Deidre.
- C. Chamath or Deidre.
- D. Chamath or Ewen.
- E. Deidre or Ewen.
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
