VCE General Maths Matrices 2016 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2016 - Exam 2
Module 1 – Matrices
Question 1 (3 marks)A travel company arranges flight (F), hotel (H), performance (P) and tour (T) bookings. Matrix \(C\) contains the number of each type of booking for a month.
\[ C = \begin{bmatrix} 85 \\ 38 \\ 24 \\ 43 \end{bmatrix} \begin{matrix} F \\ H \\ P \\ T \end{matrix} \]a. Write down the order of matrix \(C\). 1 mark
A booking fee, per person, is collected by the travel company for each type of booking. Matrix \(G\) contains the booking fees, in dollars, per booking.
\[ G = \begin{array}{c@{}c} \begin{array}{@{}cccc@{}} F & H & P & T \end{array} \\ \left[ \begin{array}{@{}cccc@{}} 40 & 25 & 15 & 30 \end{array} \right] \end{array} \]b. i. Calculate the matrix product \(J = G \times C\). 1 mark
ii. What does matrix \(J\) represent? 1 mark
The travel company has five employees, Amara (A), Ben (B), Cheng (C), Dana (D) and Elka (E). The company allows each employee to send a direct message to another employee only as shown in the communication matrix \(G\) below. The matrix \(G^2\) is also shown below.
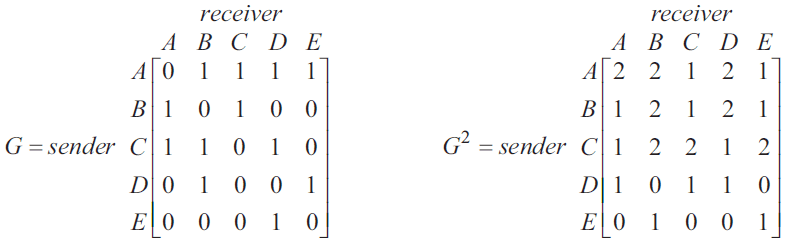
The '1' in row E, column D of matrix \(G\) indicates that Elka (sender) can send a direct message to Dana (receiver).
The '0' in row E, column C of matrix \(G\) indicates that Elka cannot send a direct message to Cheng.
a. To whom can Dana send a direct message? 1 mark
b. Cheng needs to send a message to Elka, but cannot do this directly. Write down the names of the employees who can send the message from Cheng directly to Elka. 1 mark
The travel company is studying the choice between air (A), land (L), sea (S) or no (N) travel by some of its customers each year. Matrix \(T\), shown below, contains the percentages of customers who are expected to change their choice of travel from year to year.
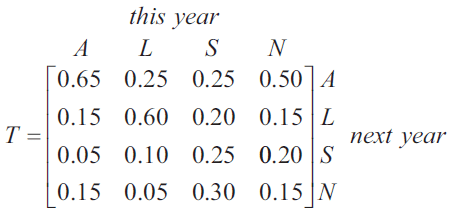
Let \(S_n\) be the matrix that shows the number of customers who choose each type of travel \(n\) years after 2014. Matrix \(S_0\) below shows the number of customers who chose each type of travel in 2014.
\[ S_0 = \begin{bmatrix} 520 \\ 320 \\ 80 \\ 80 \end{bmatrix} \begin{matrix} A \\ L \\ S \\ N \end{matrix} \]
Matrix \(S_1\) below shows the number of customers who chose each type of travel in 2015.
\[ S_1 = TS_0 = \begin{bmatrix} 478 \\ d \\ e \\ f \end{bmatrix} \begin{matrix} A \\ L \\ S \\ N \end{matrix} \]a. Write the values missing from matrix \(S_1\) (\(d, e, f\)) in the boxes provided below. 1 mark
\(d = \) \(e = \) \(f = \)
b. Write a calculation that shows that 478 customers were expected to choose air travel in 2015. 1 mark
c. Consider the customers who chose sea travel in 2014. How many of these customers were expected to choose sea travel in 2015? 1 mark
d. Consider the customers who were expected to choose air travel in 2015. What percentage of these customers had also chosen air travel in 2014? Round your answer to the nearest whole number. 1 mark
e. In 2016, the number of customers studied was increased to 1360. Matrix \(R_{2016}\), shown below, contains the number of these customers who chose each type of travel in 2016.
The company intends to increase the number of customers in the study in 2017 and in 2018. The matrix that contains the number of customers who are expected to choose each type of travel in 2017 (\(R_{2017}\)) and 2018 (\(R_{2018}\)) can be determined using the matrix equations shown below.
\(R_{2017} = TR_{2016} + B \quad R_{2018} = TR_{2017} + B\)
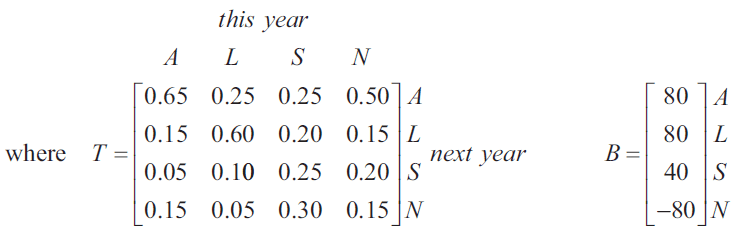
i. The element in the fourth row of matrix \(B\) is -80. Explain this number in the context of selecting customers for the studies in 2017 and 2018. 1 mark
ii. Determine the number of customers who are expected to choose sea travel in 2018. Round your answer to the nearest whole number. 2 marks
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
