VCE General Maths Matrices 2018 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 12
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2018 - Exam 2
A toll road is divided into three sections, \(E\), \(F\) and \(G\).
The cost, in dollars, to drive one journey on each section is shown in matrix \(C\) below.
\[ C = \begin{bmatrix} 3.58 \\ 2.22 \\ 2.87 \end{bmatrix} \begin{matrix} E \\ F \\ G \end{matrix} \]
a. What is the cost of one journey on section \(G\)? 1 mark
b. Write down the order of matrix \(C\). 1 mark
c. One day Kim travels once on section \(E\) and twice on section \(G\).
His total toll cost for this day can be found by the matrix product \(M \times C\).
Write down the matrix \(M\). 1 mark
\(M\) =
The Westhorn Council must prepare roads for expected population changes in each of three locations: main town (\(M\)), villages (\(V\)) and rural areas (\(R\)).
The population of each of these locations in 2018 is shown in matrix \(P_{2018}\) below.
\[ P_{2018} = \begin{bmatrix} 2100 \\ 1800 \\ 1700 \end{bmatrix} \begin{matrix} M \\ V \\ R \end{matrix} \]
The expected annual change in population in each location is shown in the table below.
| Location | main town | villages | rural areas |
| Annual change | increase by 4% | decrease by 1% | decrease by 2% |
a. Write down matrix \(P_{2019}\), which shows the expected population in each location in 2019. 1 mark
\(P_{2019}\) =
b. The expected population in each of the three locations in 2019 can be determined from the matrix product
\(P_{2019} = F \times P_{2018}\)
where \(F\) is a diagonal matrix.
Write down matrix \(F\). 1 mark
\(F\) =
The Hiroads company has a contract to maintain and improve 2700 km of highway.
Each year sections of highway must be graded (\(G\)), resurfaced (\(R\)) or sealed (\(S\)).
The remaining highway will need no maintenance (\(N\)) that year.
Let \(S_n\) be the state matrix that shows the highway maintenance schedule for the \(n\)th year after 2018.
The maintenance schedule for 2018 is shown in matrix \(S_0\) below.
\[ S_0 = \begin{bmatrix} 700 \\ 400 \\ 200 \\ 1400 \end{bmatrix} \begin{matrix} G \\ R \\ S \\ N \end{matrix} \]
The type of maintenance in sections of highway varies from year to year, as shown in the transition matrix, \(T\), below.
\[ T = \begin{array}{cc} & \begin{array}{cccc} \textit{this year} \end{array} \\ & \begin{array}{cccc} G & R & S & N \end{array} \\ \begin{matrix} G \\ R \\ S \\ N \end{matrix} & \left[ \begin{array}{cccc} 0.2 & 0.1 & 0.0 & 0.2 \\ 0.1 & 0.1 & 0.0 & 0.2 \\ 0.2 & 0.1 & 0.2 & 0.1 \\ 0.5 & 0.7 & 0.8 & 0.5 \end{array} \right] \end{array} \begin{array}{c} \textit{next year} \end{array} \]
a. Of the length of highway that was graded (\(G\)) in 2018, how many kilometres are expected to be resurfaced (\(R\)) the following year? 1 mark
b. Show that the length of highway that is to be graded (\(G\)) in 2019 is 460 km by writing the appropriate numbers in the boxes below. 1 mark
\(\times\) 700 + \(\times\) 400 + \(\times\) 200 + \(\times\) 1400 = 460
The state matrix describing the highway maintenance schedule for the \(n\)th year after 2018 is given by
\(S_{n+1} = T S_n\)
c. Complete the state matrix, \(S_1\), below for the highway maintenance schedule for 2019 (one year after 2018). 1 mark
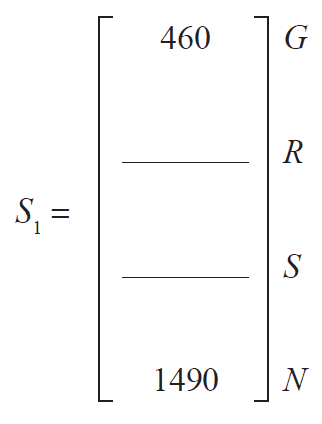
d. In 2020, 1536 km of highway is expected to require no maintenance (\(N\)).
Of these kilometres, what percentage is expected to have had no maintenance (\(N\)) in 2019?
Round your answer to one decimal place. 1 mark
e. In the long term, what percentage of highway each year is expected to have no maintenance (\(N\))?
Round your answer to one decimal place. 1 mark
Beginning in the year 2021, a new company will take over maintenance of the same 2700 km highway with a new contract.
Let \(M_n\) be the state matrix that shows the highway maintenance schedule of this company for the \(n\)th year after 2020.
The maintenance schedule for 2020 is shown in matrix \(M_0\) below.
For these 2700 km of highway, the matrix recurrence relation shown below can be used to determine the number of kilometres of this highway that will require each type of maintenance from year to year.
\(M_{n+1} = T M_n + B\)
where
\[ M_0 = \begin{bmatrix} 500 \\ 400 \\ 300 \\ 1500 \end{bmatrix} \begin{matrix} G \\ R \\ S \\ N \end{matrix}, \quad T = \begin{array}{cc} & \begin{array}{cccc} \textit{this year} \end{array} \\ & \begin{array}{cccc} G & R & S & N \end{array} \\ \begin{matrix} G \\ R \\ S \\ N \end{matrix} & \left[ \begin{array}{cccc} 0.2 & 0.1 & 0.0 & 0.2 \\ 0.1 & 0.1 & 0.0 & 0.2 \\ 0.2 & 0.1 & 0.2 & 0.1 \\ 0.5 & 0.7 & 0.8 & 0.5 \end{array} \right] \end{array} \begin{array}{c} \textit{next year} \end{array}, \quad B = \begin{bmatrix} k \\ 20 \\ 10 \\ -60 \end{bmatrix} \]
a. Write down the value of \(k\) in matrix \(B\). 1 mark
b. How many kilometres of highway are expected to be graded (\(G\)) in the year 2022? 1 mark
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
