VCE General Maths Matrices 2022 Exam 2 Mini Test
VCAA General Maths Exam 2
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 2 minutes
Writing time: 12 minutes
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In all questions where a numerical answer is required, you should only round your answer when instructed to do so.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2022 - Exam 2 (Part 1)
Matrix \(C\) shows the nightly cost, in dollars, of three types of family accommodation at a ski resort: hostel (\(H\)), motel (\(M\)) and apartment (\(A\)).
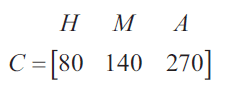
The Dwyer family is planning to stay at the ski resort for five nights.
a. Complete the matrix equation below to show the cost of staying at each type of accommodation for five nights. 1 mark
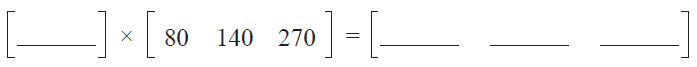
b. The family has decided to stay at the motel for two nights and in an apartment for three nights.
Write down the column matrix \(A\) for which the product matrix \(CA\) gives the total accommodation cost for the five nights. 1 mark
Students from a nearby school spend one school term skiing at the resort. One year, the school term begins on 16 July and ends on 22 September.
The resort has three different types of ski runs, each of which is classified as beginner (\(B\)), intermediate (\(I\)) or advanced (\(A\)).
Each day, the students use one of the three types of ski runs.
Matrix \(T\) below contains the proportion of students who are expected to change their choice of ski run from day to day.
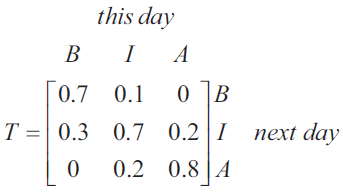
Let \(S_n\) be the matrix that shows the number of students who choose each type of ski run \(n\) days after 16 July.
Matrix \(S_0\) below shows the number of skiers who chose each type of ski run on 16 July.
\[ S_0 = \begin{bmatrix} 210 \\ 190 \\ 80 \end{bmatrix} \begin{matrix} B \\ I \\ A \end{matrix} \]
a. How many skiers are expected to choose the same ski run on 17 July? 1 mark
b. Consider the skiers who are expected to choose the advanced ski run on 17 July.
What percentage of these skiers also chose the advanced ski run on 16 July?
Round your answer to the nearest whole number. 1 mark
c. What is the maximum number of students expected to ski the intermediate ski run on any one day?
Round your answer to the nearest whole number. 1 mark
At the end of the school term, the students vote for who they want to captain the ski team for the next ski season.
Three students – Ali, Lee and Max – have been nominated for captain.
Seven days before the end of the school term, the students were asked who they planned to vote for.
The following table shows each candidate and the number of students who plan to vote for each candidate at the start of the seven days.
| Candidate | Number of people who plan to vote for the candidate |
|---|---|
| Ali | 160 |
| Lee | 140 |
| Max | 180 |
Each day all students are asked who they plan to vote for.
It is expected that students may change the candidate they plan to vote for each day over the seven days as follows. Some percentages are missing.
- 40% of students who plan to vote for Ali one day will plan to vote for Ali the next day.
- 30% of students who plan to vote for Ali one day will plan to vote for Lee the next day.
- 50% of students who plan to vote for Lee one day will plan to vote for Lee the next day.
- 30% of students who plan to vote for Lee one day will plan to vote for Max the next day.
- 50% of students who plan to vote for Max one day will plan to vote for Max the next day.
- 20% of students who plan to vote for Max one day will plan to vote for Lee the next day.
a. How many students plan to vote for Ali after one day? 1 mark
b. Max decides to withdraw his nomination after one day.
Matrix \(T\) below shows the proportion of students who change their preferred candidate from one day to the next for the remaining six days after Max withdraws his nomination.

At the end of the seven days, who is expected to become captain of the ski team and how many votes will this person receive?
Round your answer to the nearest whole number. 2 marks
End of Question and Answer Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
