VCE General Maths Matrices 2016 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2016
The transpose of \(\begin{bmatrix} 2 & 7 & 10 \\ 13 & 19 & 8 \end{bmatrix}\) is
- A. \(\begin{bmatrix} 13 & 19 & 8 \\ 2 & 7 & 10 \end{bmatrix}\)
- B. \(\begin{bmatrix} 10 & 7 & 2 \\ 8 & 19 & 13 \end{bmatrix}\)
- C. \(\begin{bmatrix} 2 & 13 \\ 7 & 19 \\ 10 & 8 \end{bmatrix}\)
- D. \(\begin{bmatrix} 13 & 2 \\ 19 & 7 \\ 8 & 10 \end{bmatrix}\)
- E. \(\begin{bmatrix} 8 & 10 \\ 19 & 7 \\ 13 & 2 \end{bmatrix}\)
The matrix product \(\begin{bmatrix} 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} L \\ E \\ A \\ P \\ S \end{bmatrix}\) is equal to
- A. \(\begin{bmatrix} L \\ A \\ P \\ S \\ E \end{bmatrix}\)
- B. \(\begin{bmatrix} L \\ E \\ A \\ P \\ S \end{bmatrix}\)
- C. \(\begin{bmatrix} P \\ L \\ E \\ A \\ S \end{bmatrix}\)
- D. \(\begin{bmatrix} P \\ A \\ L \\ E \\ S \end{bmatrix}\)
- E. \(\begin{bmatrix} P \\ E \\ A \\ L \\ S \end{bmatrix}\)
The table below shows the number of each type of coin saved in a moneybox.
| Coin | 5 cent | 10 cent | 20 cent | 50 cent |
|---|---|---|---|---|
| Number | 15 | 32 | 48 | 24 |
The matrix product that displays the total number of coins and the total value of these coins is
- A. \([5 \quad 10 \quad 20 \quad 50] \begin{bmatrix} 15 \\ 32 \\ 48 \\ 24 \end{bmatrix}\)
- B. \([15 \quad 32 \quad 48 \quad 24] \begin{bmatrix} 1 & 5 \\ 1 & 10 \\ 1 & 20 \\ 1 & 50 \end{bmatrix}\)
- C. \([5 \quad 10 \quad 20 \quad 50] \begin{bmatrix} 1 & 15 \\ 1 & 32 \\ 1 & 48 \\ 1 & 24 \end{bmatrix}\)
- D. \([15 \quad 32 \quad 48 \quad 24] \begin{bmatrix} 5 \\ 10 \\ 20 \\ 50 \end{bmatrix}\)
- E. \(\begin{bmatrix} 5 & 10 & 20 & 50 \\ 15 & 32 & 48 & 24 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 1 \\ 1 \end{bmatrix}\)
Let \(M = \begin{bmatrix} 1 & 2 & 3 & 4 \\ 3 & 4 & 5 & 6 \end{bmatrix}\)
The element in row \(i\) and column \(j\) of \(M\) is \(m_{ij}\).
The elements of \(M\) are determined by the rule
- A. \(m_{ij} = i + j - 1\)
- B. \(m_{ij} = 2i - j + 1\)
- C. \(m_{ij} = 2i + j - 2\)
- D. \(m_{ij} = i + 2j - 2\)
- E. \(m_{ij} = i + j + 1\)
Families in a country town were asked about their annual holidays.
Every year, these families choose between staying at home (\(H\)), travelling (\(T\)) and camping (\(C\)).
The transition diagram below shows the way families in the town change their holiday preferences from year to year.
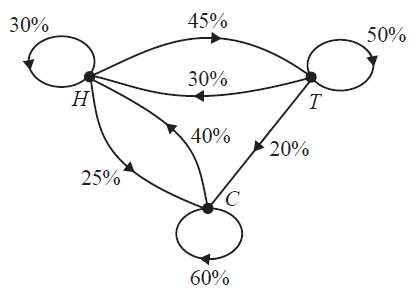
A transition matrix that provides the same information as the transition diagram is

Each week, the 300 students at a primary school choose art (\(A\)), music (\(M\)) or sport (\(S\)) as an afternoon activity.
The transition matrix below shows how the students’ choices change from week to week.
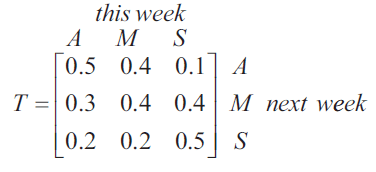
Based on the information above, it can be concluded that, in the long term
- A. no student will choose sport.
- B. all students will choose to stay in the same activity each week.
- C. all students will have chosen to change their activity at least once.
- D. more students will choose to do music than sport.
- E. the number of students choosing to do art and music will be the same.
The matrix below shows the result of each match between four teams, \(A, B, C\) and \(D\), in a bowling tournament. Each team played each other team once and there were no draws.
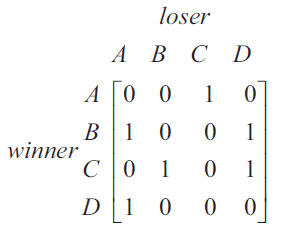
In this tournament, each team was given a ranking that was determined by calculating the sum of its one-step and two-step dominances. The team with the highest sum was ranked number one (1). The team with the second-highest sum was ranked number two (2), and so on.
Using this method, team \(C\) was ranked number one (1).
Team \(A\) would have been ranked number one (1) if the winner of one match had lost instead.
That match was between teams
- A. \(A\) and \(B\).
- B. \(A\) and \(D\).
- C. \(B\) and \(C\).
- D. \(B\) and \(D\).
- E. \(C\) and \(D\).
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
