VCE General Maths Matrices 2017 Exam 1 Mini Test

VCAA General Maths Exam 1

This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.

Number of marks: 8

Reading time: 3 minutes

Writing time: 18 minutes

Formula Sheet

Free AI Tutor

Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.

Matrices - 2017

Module 1 – Matrices

Question 1 [2017 Exam 1 M1 Q1]

Kai has a part-time job.
Each week, he earns money and saves some of this money.
The matrix below shows the amounts earned ($E$) and saved ($S$), in dollars, in each of three weeks.

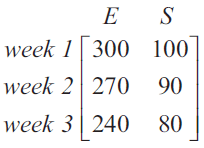
How much did Kai save in week 2?

A. $80
B. $90
C. $100
D. $170
E. $270

Question 2 [2017 Exam 1 M1 Q2]

The matrix below shows how five people, Alan ($A$), Bevan ($B$), Charlie ($C$), Drew ($D$) and Esther ($E$), can communicate with each other.

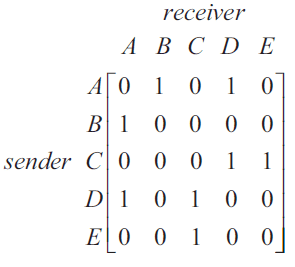
A '1' in the matrix shows that the person named in that row can send a message directly to the person named in that column.
For example, the '1' in row 3 and column 4 shows that Charlie can send a message directly to Drew.
Esther wants to send a message to Bevan.
Which one of the following shows the order of people through which the message is sent?

A. Esther – Bevan
B. Esther – Charlie – Bevan
C. Esther – Charlie – Alan – Bevan
D. Esther – Charlie – Drew – Bevan
E. Esther – Charlie – Drew – Alan – Bevan

Question 3 [2017 Exam 1 M1 Q3]

Which one of the following matrix equations has a unique solution?

A. $\begin{bmatrix} 1 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 2 \\ 10 \end{bmatrix}$
B. $\begin{bmatrix} 6 & -6 \\ -4 & 4 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 60 \\ 36 \end{bmatrix}$
C. $\begin{bmatrix} 8 & -4 \\ 4 & 2 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 12 \\ 18 \end{bmatrix}$
D. $\begin{bmatrix} 7 & 0 \\ 5 & 0 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 14 \\ 15 \end{bmatrix}$
E. $\begin{bmatrix} 4 & -2 \\ 6 & -3 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} 36 \\ 24 \end{bmatrix}$

Question 4 [2017 Exam 1 M1 Q4]

A permutation matrix, $P$, can be used to change $\begin{bmatrix} F \\ E \\ A \\ R \\ S \end{bmatrix}$ into $\begin{bmatrix} S \\ A \\ F \\ R \\ E \end{bmatrix}$.
Matrix $P$ is

A. $\begin{bmatrix} 0 & 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 & 0 \\ 1 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & 1 & 0 \end{bmatrix}$
B. $\begin{bmatrix} 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \end{bmatrix}$
C. $\begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 \end{bmatrix}$
D. $\begin{bmatrix} 1 & 0 & 0 & 0 & 1 \\ 0 & 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 & 1 \end{bmatrix}$
E. $\begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \end{bmatrix}$

Question 5 [2017 Exam 1 M1 Q5]

Four teams, $A, B, C$ and $D$, competed in a round-robin competition where each team played each of the other teams once. There were no draws.
The results are shown in the matrix below.

$ \begin{array}{cc} & \textit{loser} \\ \textit{winner} & \begin{array}{c@{}c} & \begin{array}{@{}cccc@{}} A & B & C & D \end{array} \\ \begin{matrix} A \\ B \\ C \\ D \end{matrix} & \left[ \begin{array}{@{}cccc@{}} 0 & 0 & f & 1 \\ 1 & 0 & 0 & 0 \\ 1 & g & 0 & 1 \\ 0 & 1 & 0 & h \end{array} \right] \end{array} \end{array} $

A '1' in the matrix shows that the team named in that row defeated the team named in that column.
For example, the '1' in row 2 shows that team $B$ defeated team $A$.
In this matrix, the values of $f, g$ and $h$ are

A. $f = 0, \quad g = 1, \quad h = 0$
B. $f = 0, \quad g = 1, \quad h = 1$
C. $f = 1, \quad g = 0, \quad h = 0$
D. $f = 1, \quad g = 1, \quad h = 0$
E. $f = 1, \quad g = 1, \quad h = 1$

Question 6 [2017 Exam 1 M1 Q6]

The table below shows information about two matrices, $A$ and $B$.

Matrix	Order	Rule
$A$	$3 \times 3$	$a_{ij} = 2i + j$
$B$	$3 \times 3$	$b_{ij} = i - j$

The element in row $i$ and column $j$ of matrix $A$ is $a_{ij}$.
The element in row $i$ and column $j$ of matrix $B$ is $b_{ij}$.
The sum $A + B$ is

A. $\begin{bmatrix} 5 & 7 & 9 \\ 8 & 10 & 12 \\ 11 & 13 & 15 \end{bmatrix}$
B. $\begin{bmatrix} 5 & 8 & 11 \\ 7 & 10 & 13 \\ 9 & 12 & 15 \end{bmatrix}$
C. $\begin{bmatrix} 3 & 6 & 9 \\ 3 & 6 & 9 \\ 3 & 6 & 9 \end{bmatrix}$
D. $\begin{bmatrix} 3 & 3 & 3 \\ 6 & 6 & 6 \\ 9 & 9 & 9 \end{bmatrix}$
E. $\begin{bmatrix} 3 & 6 & 3 \\ 6 & 3 & 9 \\ 3 & 9 & 3 \end{bmatrix}$

Question 7 [2017 Exam 1 M1 Q7]

At a fish farm:

young fish ($Y$) may eventually grow into juveniles ($J$) or they may die ($D$)
juveniles ($J$) may eventually grow into adults ($A$) or they may die ($D$)
adults ($A$) eventually die ($D$).

The initial state of this population, $F_0$, is shown below.

$ F_0 = \begin{bmatrix} 50\,000 \\ 10\,000 \\ 7000 \\ 0 \end{bmatrix} \begin{matrix} Y \\ J \\ A \\ D \end{matrix} $

Every month, fish are either sold or bought so that the number of young, juvenile and adult fish in the farm remains constant.
The population of fish in the fish farm after $n$ months, $F_n$, can be determined by the recurrence rule

$ F_{n+1} = \begin{bmatrix} 0.65 & 0 & 0 & 0 \\ 0.25 & 0.75 & 0 & 0 \\ 0 & 0.20 & 0.95 & 0 \\ 0.10 & 0.05 & 0.05 & 1 \end{bmatrix} F_n + B $

where $B$ is a column matrix that shows the number of young, juvenile and adult fish bought or sold each month and the number of dead fish that are removed.
Each month, the fish farm will

A. sell 1650 adult fish.
B. buy 1750 adult fish.
C. sell 17 500 young fish.
D. buy 50 000 young fish.
E. buy 10 000 juvenile fish.

Question 8 [2017 Exam 1 M1 Q8]

Consider the matrix recurrence relation below.

$ S_0 = \begin{bmatrix} 40 \\ 15 \\ 20 \end{bmatrix}, \quad S_{n+1} = T S_n \quad \text{where } T = \begin{bmatrix} 0.3 & 0.2 & V \\ 0.2 & 0.2 & W \\ X & Y & Z \end{bmatrix} $

Matrix $T$ is a regular transition matrix.
Given the above and that $S_1 = \begin{bmatrix} 29 \\ 13 \\ 33 \end{bmatrix}$, which one of the following expressions is not true?

A. $W > Z$
B. $Y > X$
C. $V > Y$
D. $V + W + Z = 1$
E. $X + Y + Z > 1$

End of Multiple-Choice Question Book

VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

Matrix	Order	Rule
\(A\)	\(3 \times 3\)	\(a_{ij} = 2i + j\)
\(B\)	\(3 \times 3\)	\(b_{ij} = i - j\)