VCE General Maths Matrices 2018 Exam 1 Mini Test
VCAA General Maths Exam 1
This is the full VCE General Maths Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 8
Reading time: 3 minutes
Writing time: 18 minutes
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Matrices - 2018
Which one of the following matrices has a determinant of zero?
- A. \(\begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix}\)
- B. \(\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)
- C. \(\begin{bmatrix} 1 & 2 \\ -3 & 6 \end{bmatrix}\)
- D. \(\begin{bmatrix} 3 & 6 \\ 2 & 4 \end{bmatrix}\)
- E. \(\begin{bmatrix} 4 & 0 \\ 0 & -2 \end{bmatrix}\)
The matrix product \(\begin{bmatrix} 4 & 2 & 0 \end{bmatrix} \times \begin{bmatrix} 4 \\ 12 \\ 8 \end{bmatrix}\) is equal to
- A. \(\begin{bmatrix} 144 \end{bmatrix}\)
- B. \(\begin{bmatrix} 16 \\ 24 \\ 0 \end{bmatrix}\)
- C. \(4 \times \begin{bmatrix} 1 & 2 & 0 \end{bmatrix} \times \begin{bmatrix} 12 \\ 8 \end{bmatrix}\)
- D. \(2 \times \begin{bmatrix} 2 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 6 \\ 4 \end{bmatrix}\)
- E. \(4 \times \begin{bmatrix} 2 & 1 & 0 \end{bmatrix} \times \begin{bmatrix} 2 \\ 6 \\ 4 \end{bmatrix}\)
Five people, India (I), Jackson (J), Krishna (K), Leanne (L) and Mustafa (M), competed in a table tennis tournament.
Each competitor played every other competitor once only.
Each match resulted in a winner and a loser.
The matrix below shows the tournament results.
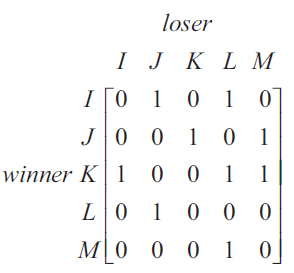
A ‘1’ in the matrix shows that the competitor named in that row defeated the competitor named in that column.
For example, the ‘1’ in the fourth row shows that Leanne defeated Jackson.
A ‘0’ in the matrix shows that the competitor named in that row lost to the competitor named in that column.
There is an error in the matrix. The winner of one of the matches has been incorrectly recorded as a ‘0’.
This match was between
- A. India and Mustafa.
- B. India and Krishna.
- C. Krishna and Leanne.
- D. Leanne and Mustafa.
- E. Jackson and Mustafa.
Matrix \(P\) is a \(4 \times 4\) permutation matrix.
Matrix \(W\) is another matrix such that the matrix product \(P \times W\) is defined.
This matrix product results in the entire first and third rows of matrix \(W\) being swapped.
The permutation matrix \(P\) is
- A. \(\begin{bmatrix} 0 & 0 & 0 & 1 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
- B. \(\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
- C. \(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\)
- D. \(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}\)
- E. \(\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}\)
Liam cycles, runs, swims and walks for exercise several times a month.
Each time he cycles, Liam covers a distance of \(c\) kilometres.
Each time he runs, Liam covers a distance of \(r\) kilometres.
Each time he swims, Liam covers a distance of \(s\) kilometres.
Each time he walks, Liam covers a distance of \(w\) kilometres.
The number of times that Liam cycled, ran, swam and walked each month over a four-month period, and the total distance that Liam travelled in each of those months, are shown in the table below.
| Number of times in a month | Total distance for a month (km) | ||||
|---|---|---|---|---|---|
| Cycle | Run | Swim | Walk | ||
| Month 1 | 5 | 7 | 6 | 8 | 160 |
| Month 2 | 8 | 6 | 9 | 7 | 172 |
| Month 3 | 7 | 8 | 7 | 6 | 165 |
| Month 4 | 8 | 8 | 5 | 5 | 162 |
The matrix that contains the distance each time Liam cycled, ran, swam and walked, \(\begin{bmatrix} c \\ r \\ s \\ w \end{bmatrix}\), is
- A. \(\begin{bmatrix} 5 \\ 6 \\ 7 \\ 5 \end{bmatrix}\)
- B. \(\begin{bmatrix} 8 \\ 6 \\ 1 \\ 9 \end{bmatrix}\)
- C. \(\begin{bmatrix} 8 \\ 6 \\ 7 \\ 9 \end{bmatrix}\)
- D. \(\begin{bmatrix} 8 \\ 8 \\ 9 \\ 8 \end{bmatrix}\)
- E. \(\begin{bmatrix} 4290 \\ 4931 \\ 4623 \\ 4291 \end{bmatrix}\)
A transition matrix, \(V\), is shown below.
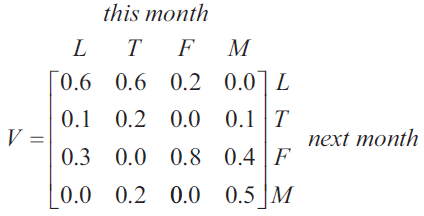
The transition diagram below has been constructed from the transition matrix \(V\).
The labelling in the transition diagram is not yet complete.
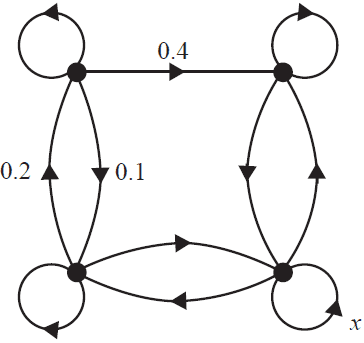
The proportion for one of the transitions is labelled \(x\).
The value of \(x\) is
- A. 0.2
- B. 0.5
- C. 0.6
- D. 0.7
- E. 0.8
A study of the antelope population in a wildlife park has shown that antelope regularly move between three locations, east (E), north (N) and west (W).
Let \(A_n\) be the state matrix that shows the population of antelope in each location \(n\) months after the study began.
The expected population of antelope in each location can be determined by the matrix recurrence rule
\(A_{n+1} = TA_n - D\)
where
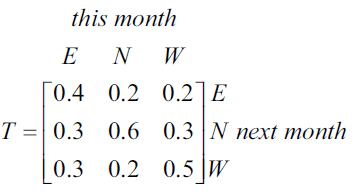
and
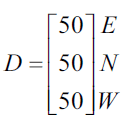
The state matrix, \(A_3\), below shows the population of antelope three months after the study began.
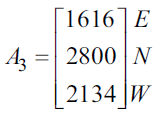
The number of antelope in the west (W) location two months after the study began, as found in the state matrix \(A_2\), is closest to
- A. 2060
- B. 2130
- C. 2200
- D. 2240
- E. 2270
A public library organised 500 of its members into five categories according to the number of books each member borrows each month.
These categories are
\(J\) = no books borrowed per month
\(K\) = one book borrowed per month
\(L\) = two books borrowed per month
\(M\) = three books borrowed per month
\(N\) = four or more books borrowed per month
The transition matrix, \(T\), below shows how the number of books borrowed per month by the members is expected to change from month to month.
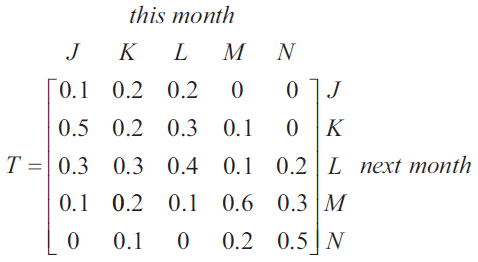
In the long term, which category is expected to have approximately 96 members each month?
- A. J
- B. K
- C. L
- D. M
- E. N
End of Multiple-Choice Question Book
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au
