SACE Stage 2 Maths Methods Topic Tests
Differential Calculus Topic Test 1
Number of marks: 12
Writing time: 15 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
(a) Consider the functions \(f(x) = e^x - 4e^{2x}\) and \(g(x) = e^{3x} - 4e^{2x}\). Figure 7 shows the graph of \(y=f(x)\) and Figure 8 shows the graph of \(y=g(x)\) with the stationary point of each function labelled as \(P\) and \(Q\) respectively.
Complete Table 4 below by finding the \(y\)-coordinates of \(P\) and \(Q\). (2 marks)
| Point | \(y\)-coordinate |
|---|---|
| \(P\) | |
| \(Q\) |
(b) Consider the function \(y = e^{ax} - 4e^{2x}\) where \(a\) is a positive constant such that \(a \ne 2\).
(i) Show that the \(x\)-coordinate of the only stationary point of \(y = e^{ax} - 4e^{2x}\) is \(x = \frac{1}{a-2}\ln\left(\frac{8}{a}\right)\). (4 marks)
(ii) (1) Show that the \(y\)-coordinate of the stationary point of \(y = e^{ax} - 4e^{2x}\) is \(y = 4\left(\frac{8}{a}\right)^{\frac{2}{a-2}}\left(\frac{2-a}{a}\right)\). (4 marks)
(2) Determine the values of \(a\) for which the \(y\)-coordinate of the stationary point of the function \(y = e^{ax} - 4e^{2x}\) is positive. Justify your answer. (2 marks)
end of booklet
Differential Calculus Topic Test 2
Number of marks: 10
Writing time: 13 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Consider the function \(f(x) = \frac{1}{x^2}\).
(a) Use an algebraic approach to determine the equation of the tangent to \(f(x)\) at \(x=1\). (3 marks)
(b) Determine the \(x\)-intercept of this tangent. (1 mark)
Consider the function \(g(x) = \frac{1}{x^2+k}\), where \(k\) is a non-negative constant. The \(x\)-intercept of the tangent to \(g(x)\) at \(x=1\) is shown in Table 1 for various values of \(k\).
| \(k\) | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| \(g(x)\) | \(\frac{1}{x^2+1}\) | \(\frac{1}{x^2+2}\) | \(\frac{1}{x^2+3}\) | \(\frac{1}{x^2+4}\) |
| \(x\)-intercept of the tangent to \(g(x)\) at \(x=1\) | \((2,0)\) | \(\left(\frac{5}{2}, 0\right)\) | \((3,0)\) | \(\left(\frac{7}{2}, 0\right)\) |
(c) Make a conjecture about the \(x\)-intercept of the tangent to \(g(x) = \frac{1}{x^2+k}\) at \(x=1\). (1 mark)
(d) Prove or disprove the conjecture that you made in part (c). (5 marks)
end of booklet
Differential Calculus Topic Test 3
Number of marks: 6
Writing time: 8 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Consider the function \(f(x) = \ln(x+3)\) where \(x > -3\). A graph of \(y = f(x)\) is shown in Figure 3.
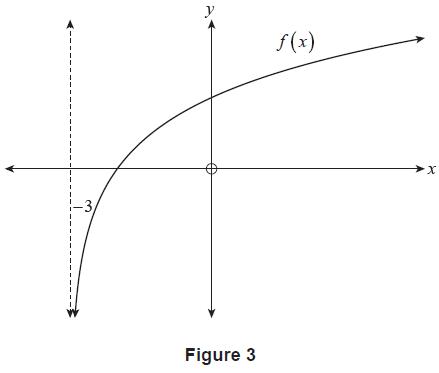
(a) Determine \(f'(x)\). (1 mark)
(b) Calculate \(f'(0)\). (1 mark)
Let \(g(x) = b\ln(x+3)\), where \(x > -3\) and \(b\) is a positive constant.
Figure 4 shows the graph of \(y=f'(x)\) and \(y=g'(x)\). The \(y\)-intercepts of each graph are labelled \(A\) and \(B\) respectively.
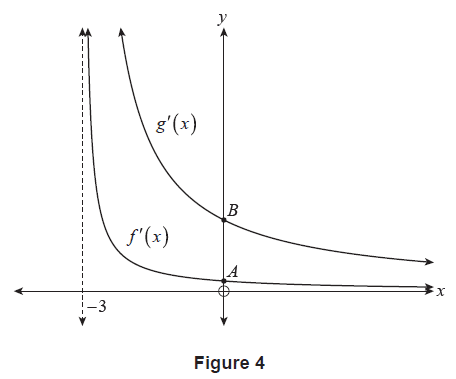
(c) The vertical distance between points \(A\) and \(B\) is 2 units. Determine the value of \(b\). (3 marks)
(d) Hence or otherwise, state the transformation applied to \(f(x)\) to obtain \(g(x)\). (1 mark)
Consider the function \(f(x) = \frac{x}{x-2}\), where \(x \ne 2\).
(a) Use first principles to find \(f'(x)\). (4 marks)
(b) Hence or otherwise, state the slope of the tangent to \(f(x)\) when \(x=6\). (1 mark)
end of booklet
Differential Calculus Topic Test 4
Number of marks: 10
Writing time: 13 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
A self-balancing robot uses a device called a PID controller to stop itself from falling over after being placed on its wheels and released. Let \(L(t)\) represent the angle of lean of the robot, at \(t\) seconds after release, where \(L(t)\) is measured in radians. Side-on diagrams of this robot in Figure 6 show various angles of lean, where:
- negative values of \(L(t)\) mean the robot has an angle of lean to the left
- \(L(t) = 0\) means the robot is vertical
- positive values of \(L(t)\) mean the robot has an angle of lean to the right.
This image cannot be reproduced here for copyright reasons.
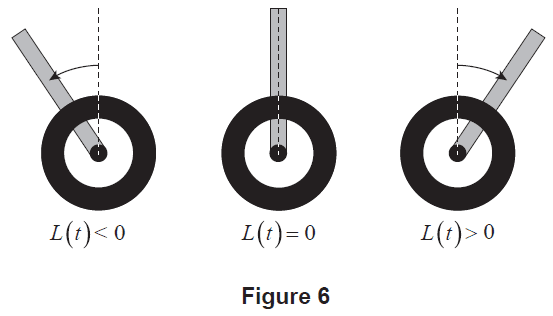
Figure 6
The PID controller's settings can be adjusted to change how long it takes the robot to reach an approximately stable vertical position after initially being placed on its wheels and released. Engineers conducted an experiment using different settings on the PID controller, starting with Setting A.
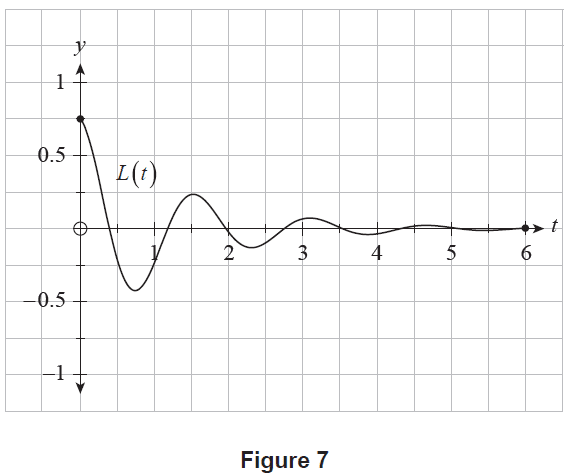
(a) Using Setting A, the robot was initially placed on its wheels and released. The resulting angle of lean was recorded for 6 seconds. Using this setting, the angle of lean of the robot, \(L(t)\), at \(t\) seconds after release, can be modelled by the function \[ L(t) = 0.75e^{-0.75t} \cos(4t), \text{ where } 0 \le t \le 6. \] A graph of \(y=L(t)\) for Setting A is shown in Figure 7.

Figure 7
(i) State the initial angle of lean of the robot, according to the model. (1 mark)
(ii) Determine the value of \(L'(1.3)\). (1 mark)
(iii) Interpret your answer to part (a)(ii) in the context of the problem, stating the appropriate units. (2 marks)
(iv) Calculate how long after being released the robot is leaning to the left with its maximum angle, according to the model. (1 mark)
(b) The engineers were not satisfied with how long the robot took to reach an approximately stable vertical state using Setting A. To improve results, the experiment was repeated using Setting B and the same initial angle of lean. Using Setting B, the angle of lean of the robot, \(L(t)\), at \(t\) seconds after release, can now be modelled by the new function \[ L(t) = 0.75e^{-t} \cos t, \text{ where } 0 \le t \le 6. \] A graph of \(y=L(t)\) for Setting B is shown in Figure 8.
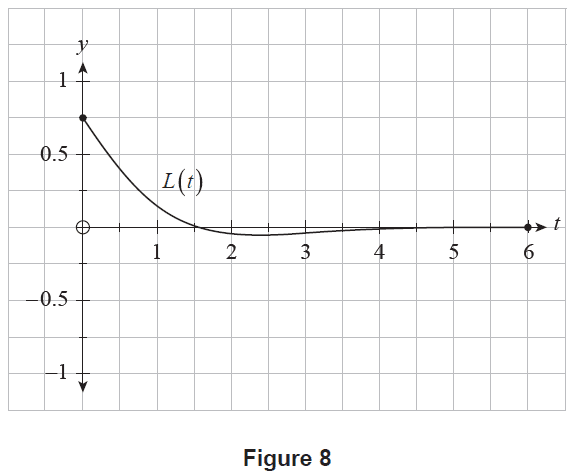
Figure 8
(i) Determine \(L'(t)\) for Setting B. (2 marks)
(ii) Hence, for Setting B, use an algebraic approach to determine the exact values of \(t\) such that \(L'(t)=0\), during the first 6 seconds after release. (3 marks)
end of booklet
Differential Calculus Topic Test 5
Number of marks: 8
Writing time: 10 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Consider the graph of the function \(y=f(x)\) shown in Figure 4 where \(f(x)\) is defined for all real values of \(x\). This function has exactly:
- two stationary points, located at \(B(b, f(b))\) and \(D(d, f(d))\)
- two inflection points, located at \(A(a, f(a))\) and \(C(c, f(c))\)
- two \(x\)-intercepts, located at \(B(b, f(b))\) and \(E(e, f(e))\).
As \(x\) increases for \(x > d\), the slope of \(f(x)\) approaches \(k\), where \(k < 0\). Additionally, \(f''(x)=0\) only at \(x=a\) and \(x=c\).
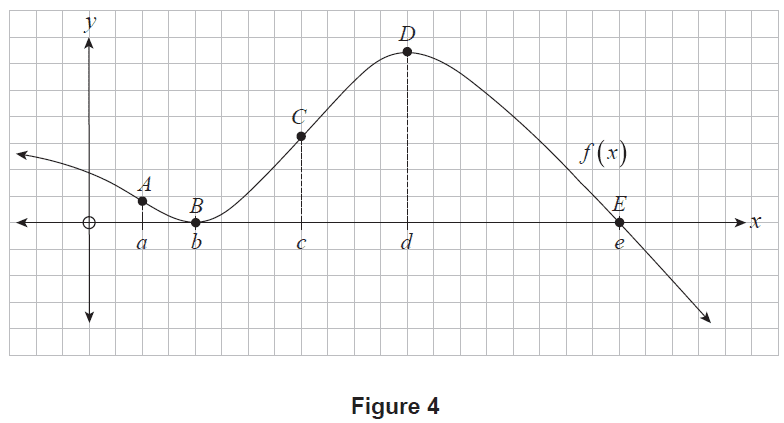
Figure 4
(a) Complete the sign diagram below for \(f'(x)\). (2 marks)
\(f'(x)\)
(b) (i) Which one statement is true? Tick the appropriate box to indicate your answer. (1 mark)
\(f'(0) < f'(a)\)
\(f'(0) = f'(a)\)
\(f'(0) > f'(a)\)
(ii) Which one statement is true? Tick the appropriate box to indicate your answer. (1 mark)
\(f(d) < 0\) and \(f''(d) < 0\)
\(f(d) < 0\) and \(f''(d) > 0\)
\(f(d) > 0\) and \(f''(d) < 0\)
\(f(d) > 0\) and \(f''(d) > 0\)
(c) State the interval(s) of \(x\) for which \(f''(x) \ge 0\). (1 mark)
(d) On Figure 5, sketch a possible graph of \(y=f'(x)\). Note that \(k\) has been added to the \(y\)-axis. (3 marks)
Figure 5
end of booklet
Differential Calculus Topic Test 6
Number of marks: 12
Writing time: 15 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
(a) Consider the function \(f(x) = \frac{2}{x-1} + 2x\), where \(x \ne 1\). A graph of \(y=f(x)\) is shown in Figure 3, with its two stationary points shown at \(A\) and \(B\).
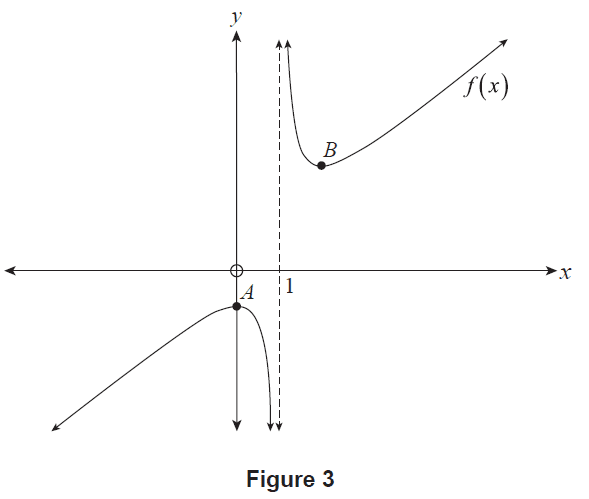
Figure 3
(i) Show that \(f'(x) = \frac{2x^2 - 4x}{(x-1)^2}\). (3 marks)
(ii) Hence, use an algebraic approach to show that \(f(x)\) has exactly two stationary points, at \(x=0\) and \(x=2\). (2 marks)
(b) Consider the function \(g(x) = \frac{2}{x-m} + 2x\), where \(m\) is a constant and \(x \ne m\).
(i) Complete the following table for each given value of \(m\). (2 marks)
| \(m\) | Function | \(x\)-coordinates of the two stationary points of the function \(g(x)\) |
|---|---|---|
| 1 | \(g(x) = \frac{2}{x-1} + 2x\) | \(x=0, x=2\) |
| 2 | \(g(x) = \frac{2}{x-2} + 2x\) | |
| 3 | \(g(x) = \frac{2}{x-3} + 2x\) | |
| 4 | \(g(x) = \frac{2}{x-4} + 2x\) |
(ii) Make a conjecture about the \(x\)-coordinates of the two stationary points of the function \(g(x) = \frac{2}{x-m} + 2x\). (1 mark)
(iii) Prove or disprove your conjecture. (4 marks)
end of booklet
Differential Calculus Topic Test 7
Number of marks: 7
Writing time: 9 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Consider the function \(f(x) = kx^2 + 1\), where \(k\) is a non-zero constant.
(a) Using first principles, show that \(f'(x) = 2kx\). (3 marks)
Figure 2 shows the graph of \(y = f(x)\) for a certain value of \(k\). The tangent to the graph at \(x=2\) is also shown. This tangent has a \(y\)-intercept at \(A\).
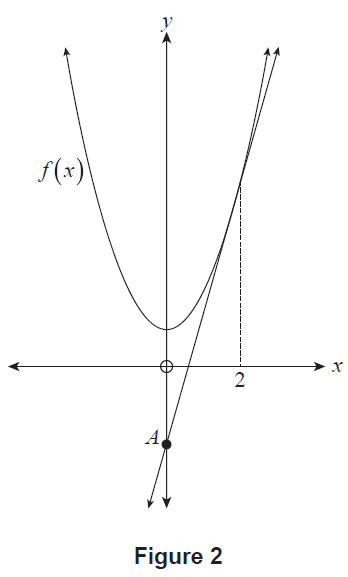
Figure 2
(b) Show that the tangent to the graph of \(y=f(x)\) at \(x=2\) has the equation \(y = 4kx - 4k + 1\). (3 marks)
(c) If the \(y\)-coordinate of \(A\) is \(-11\), determine the value of \(k\). (1 mark)
end of booklet
Differential Calculus Topic Test 8
Number of marks: 11
Writing time: 14 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Let \(f(x) = \sqrt{8-x^3}\) for \(x < 2\).
(a) Show that \(f'(x) = \frac{-3x^2}{2\sqrt{8-x^3}}\) for \(x<2\). (1 mark)
The graph of \(y=f(x)\) is shown in Figure 9, along with the normal to the graph at \(x=-1\).
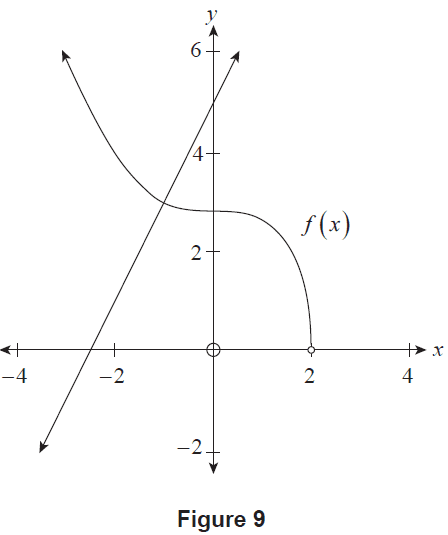
Figure 9
(b) (i) Show that the normal to the graph of \(y=f(x)\) at \(x=-1\) has the equation \(2x-y=-5\). (3 marks)
(ii) State the \(x\)-intercept of the normal \(2x-y=-5\). (1 mark)
(c) Consider the normal to the graph of \(y=f(x)\) at \(x=a\), where \(a < 2\).
(i) Show that the \(x\)-intercept of this normal is \(x = a - \frac{3}{2}a^2\). (4 marks)
(ii) Hence, using an algebraic approach, find the value of \(a\) such that the \(x\)-intercept of this normal is maximised. (2 marks)
end of booklet
Differential Calculus Topic Test 9
Number of marks: 9
Writing time: 12 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
The graph of \(y=x\ln x - x\) where \(x>0\) is shown in Figure 6.
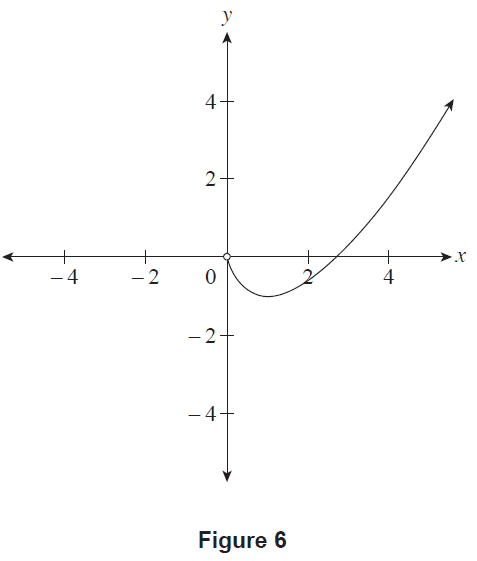
Figure 6
(a) (i) Show that \(\frac{dy}{dx} = \ln x\). (1 mark)
(ii) Hence, using an algebraic approach, determine the \(y\)-coordinate of the stationary point of \(y=x\ln x - x\). (2 marks)
Consider the family of functions of the form \(y = x\ln x - x + (\ln k)x\), where \(x>0\) and \(k\) is a positive constant. Each function in this family has a stationary point at \(A\), as shown in Figure 7.
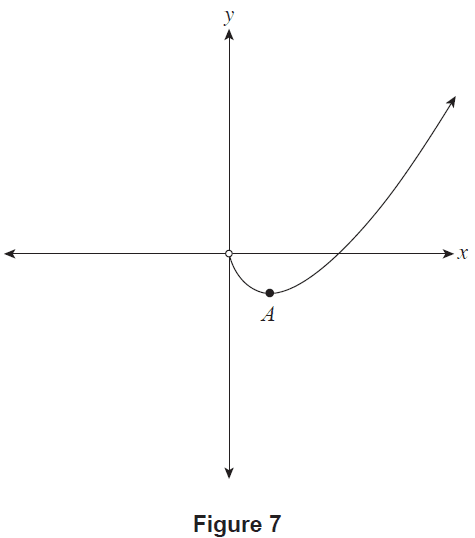
Figure 7
(b) Complete the table below by finding the \(y\)-coordinates of \(A\) for \(y = x\ln x - x + (\ln k)x\) where \(k=1, 2, 3,\) and \(4\). (1 mark)
| \(k\) | Function | \(y\)-coordinate of \(A\) |
|---|---|---|
| 1 | \(x\ln x - x\) | |
| 2 | \(x\ln x - x + (\ln 2)x\) | |
| 3 | \(x\ln x - x + (\ln 3)x\) | |
| 4 | \(x\ln x - x + (\ln 4)x\) |
(c) Hence, make a conjecture for the \(y\)-coordinate of \(A\), for any value of \(k\). (1 mark)
(d) Prove or disprove your conjecture. (4 marks)
end of booklet
Differential Calculus Topic Test 10
Number of marks: 15
Writing time: 20 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
Consider the function \(f(x)\) for \(x \ge 0\) and \(x \ne 4\). The graph of \(y=f(x)\) is shown in Figure 1. Points \(A\) and \(C\) are the function's only stationary points, with \(x\)-coordinates of \(x=1\) and \(x=3\) respectively. Point \(B\) is the function's only inflection point, with an \(x\)-coordinate of \(x=2\). The function also has a vertical asymptote with equation \(x=4\).
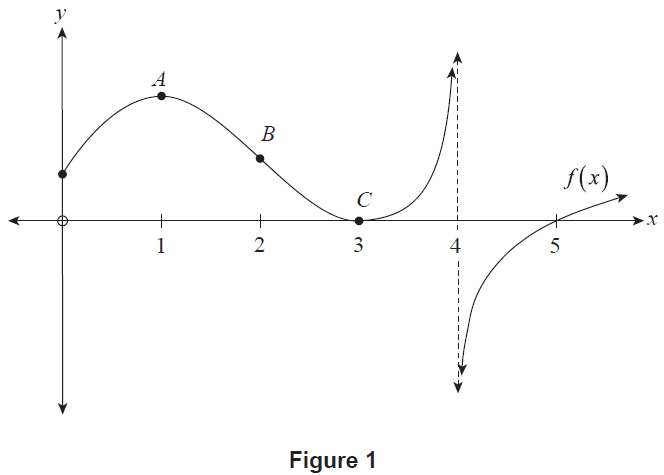
Figure 1
(a) (i) Complete the sign diagram below for \(f'(x)\). (2 marks)
\(f'(x)\)
(ii) Complete the sign diagram below for \(f''(x)\). (2 marks)
\(f''(x)\)
(b) On the axes in Figure 2, sketch a possible graph of \(y=f'(x)\). (3 marks)
Figure 2
Consider the function \(f(x) = \cos\left(\frac{1}{5}x^2 - 1\right)\) for \(0 \le x \le \pi\). Figure 3 shows the graph of \(y=f(x)\), which has two stationary points: one located at \(x=0\), and the other located at \(x=a\), where \(0 < a < \pi\).
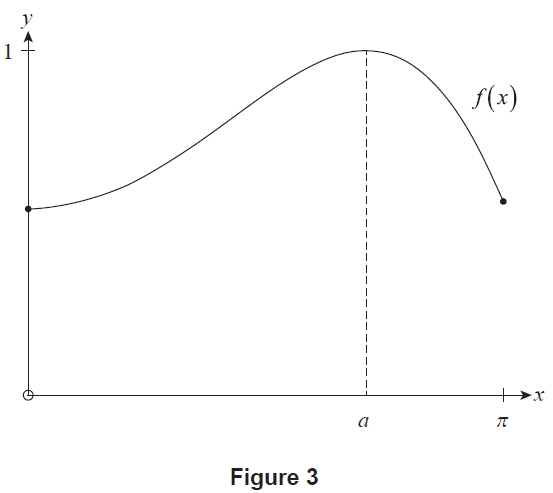
Figure 3
(a) State the nature of the stationary point located at \(x=a\). (1 mark)
(b) (i) Determine \(f'(x)\). (2 marks)
(ii) Hence, using an algebraic approach, determine the exact value of \(a\). (3 marks)
(iii) State the interval of \(x\) for which \(f(x)\) is increasing. (1 mark)
(iv) Given that \(f(x)\) has no inflection points to the right of the stationary point located at \(x=a\), state the \(x\)-coordinate(s) where \(f(x)\) is decreasing the most rapidly. (1 mark)
end of booklet


