2022 SACE Stage 2 Maths Methods Exam Paper
Question Book 1 & Question Book 2
This is a full SACE Stage 2 Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official SACE exams split into short tests you can do anytime.
Number of marks: 100
Writing time: 130 minutes
Instructions
• Show appropriate working and steps of logic in the question booklets
• State all answers correct to three significant figures, unless otherwise instructed
• Use black or blue pen
• You may use a sharp dark pencil for diagrams and graphical representations
(a) Using first principles, find \(f'(x)\) if \(f(x) = x^2 - 3\). (3 marks)
(b) Determine \(\frac{dy}{dx}\) for the following two functions. You do not need to simplify your answers.
(i) \(y = 3x^4 + (7+\sin x)^3\) (3 marks)
(ii) \(y = \frac{\ln(x^5+1)}{e^x}\) (3 marks)
(c) Determine \(\int \left(\frac{1}{x-3} + 4\right) dx\), where \(x > 3\). (2 marks)
The leading digit of a number is defined as the left-most non-zero digit. In the numbers given below, for example, 7 is the leading digit.
712 \(\qquad\) 74.2 \(\qquad\) 0.00798
Let \(X\) represent the leading digit of a naturally occurring number. Benford's law states that the leading digits in large sets of naturally occurring numbers are distributed as follows:
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| \(\Pr(X=x)\) | 0.301 | 0.176 | 0.125 | 0.097 | 0.079 | 0.067 | 0.058 | 0.051 | 0.046 |
(a) What property of the values in the table above mean that \(X\) is not uniformly distributed? (1 mark)
(b) Determine the probability of randomly selecting a naturally occurring number with a leading digit of 6 or greater. (1 mark)
(c) Identify which of the following provides a correct calculation for the mean of the leading digit of a naturally occurring number, \(\mu_X\). Tick the appropriate box. (1 mark)
\(\mu_X = 1^2(0.301) + 2^2(0.176) + 3^2(0.125) + 4^2(0.097) + 5^2(0.079) + 6^2(0.067) + 7^2(0.058) + 8^2(0.051) + 9^2(0.046)\)
\(\mu_X = 1(0.301) + 2(0.176) + 3(0.125) + 4(0.097) + 5(0.079) + 6(0.067) + 7(0.058) + 8(0.051) + 9(0.046)\)
\(\mu_X = \frac{0.301+0.176+0.125+0.097+0.079+0.067+0.058+0.051+0.046}{9}\)
(d) Benford's law can be used to detect fraudulent financial records. Further investigation of a company's financial records is undertaken if a calculated 95% confidence interval supports the claim that the mean of the leading digit of the financial records is greater than 3.441.
Consider a random sample of 250 numbers from a company's records. The mean of the leading digit in this sample is \(\bar{x} = 3.816\).
(i) Calculate a 95% confidence interval for the mean of the leading digit of the company's financial records, using the random sample described above. Assume that the standard deviation is \(\sigma_X = 2.462\). (2 marks)
(ii) Does this 95% confidence interval suggest that further investigation should be undertaken? Justify your answer. (2 marks)
Consider the function \(f(x)\) for \(x \ge 0\) and \(x \ne 4\). The graph of \(y=f(x)\) is shown in Figure 1. Points \(A\) and \(C\) are the function's only stationary points, with \(x\)-coordinates of \(x=1\) and \(x=3\) respectively. Point \(B\) is the function's only inflection point, with an \(x\)-coordinate of \(x=2\). The function also has a vertical asymptote with equation \(x=4\).
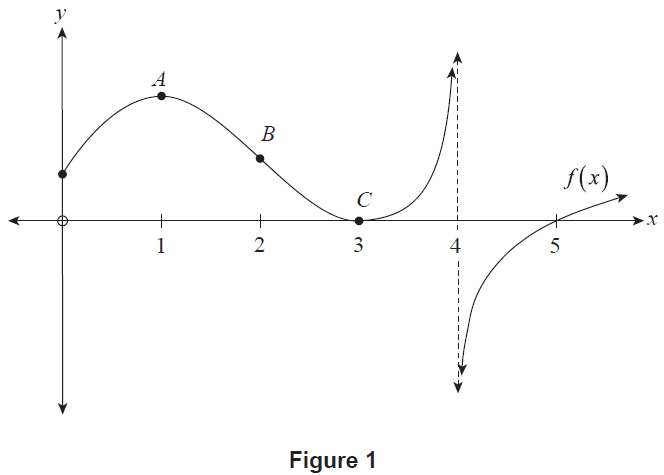
Figure 1
(a) (i) Complete the sign diagram below for \(f'(x)\). (2 marks)
\(f'(x)\)
(ii) Complete the sign diagram below for \(f''(x)\). (2 marks)
\(f''(x)\)
(b) On the axes in Figure 2, sketch a possible graph of \(y=f'(x)\). (3 marks)
Figure 2
The fat content in grams, \(X\), per carton of Ted's Oat Milk can be modelled using a normal distribution with a mean of \(\mu_X = 2.7\) g and a standard deviation of \(\sigma_X = 0.35\) g.
(a) Determine the probability that a carton of Ted's Oat Milk will contain:
(i) at least 2.8 g of fat. (1 mark)
(ii) between 1 g and 3 g of fat. (1 mark)
(b) Ted's Oat Milk is sold in packs of six cartons. Let \(S_6\) represent the distribution of fat content in one six-pack of Ted's Oat Milk.
(i) Explain why \(S_6\) can be modelled by a normal distribution. (1 mark)
(ii) Show that the distribution of \(S_6\) has a mean of \(\mu_{S_6} = 16.2\) g and a standard deviation of \(\sigma_{S_6} = 0.857\) g (correct to three significant figures). (2 marks)
(iii) Hence, determine the probability that a six-pack of Ted's Oat Milk will contain less than 18 g of fat. (1 mark)
(c) Find the value of \(k\) if \(\Pr(Z < k) = 0.99\), given that \(Z \sim N(0,1)\). (1 mark)
(d) The label on the side of a six-pack of Ted's Oat Milk states that: 'Each pack of 6 contains less than 18 g of fat.'
The company would like this statement to be true for at least 99% of Ted's Oat Milk six-packs and it is considering improvements to the manufacturing process. Although it cannot change the mean fat content of a six-pack through these improvements, the standard deviation can be reduced.
Using your answer to part (c), determine the largest possible value of \(\sigma_{S_6}\) that will result in at least 99% of six-packs containing less than 18 g of fat. Assume that \(\mu_{S_6} = 16.2\) g.

Consider the function \(f(x) = \cos\left(\frac{1}{5}x^2 - 1\right)\) for \(0 \le x \le \pi\). Figure 3 shows the graph of \(y=f(x)\), which has two stationary points: one located at \(x=0\), and the other located at \(x=a\), where \(0 < a < \pi\).
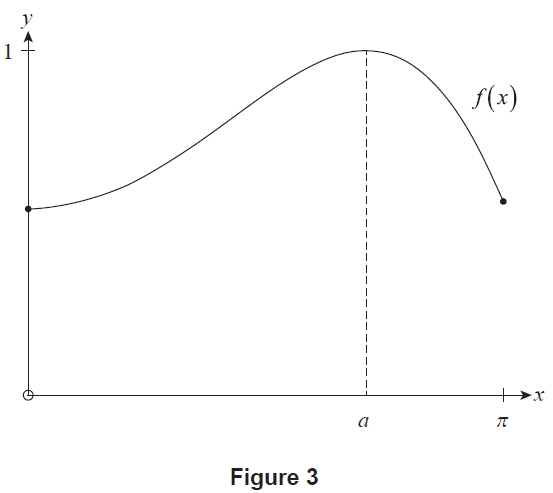
Figure 3
(a) State the nature of the stationary point located at \(x=a\). (1 mark)
(b) (i) Determine \(f'(x)\). (2 marks)
(ii) Hence, using an algebraic approach, determine the exact value of \(a\). (3 marks)
(iii) State the interval of \(x\) for which \(f(x)\) is increasing. (1 mark)
(iv) Given that \(f(x)\) has no inflection points to the right of the stationary point located at \(x=a\), state the \(x\)-coordinate(s) where \(f(x)\) is decreasing the most rapidly. (1 mark)
The rate at which medical samples arrive at a laboratory \(t\) hours after 8.00 am on a particular day can be modelled using the function \[ m(t) = 500t\sqrt{t} e^{-0.9t} \text{ for } 0 \le t \le 9, \] where the rate at which medical samples arrive at the laboratory, \(m(t)\), is measured in samples per hour.

(a) (i) Show that \(m'(t) = 750\sqrt{t}e^{-0.9t} - 450t\sqrt{t}e^{-0.9t}\). (2 marks)
(ii) Hence, using an algebraic approach, show that the rate at which medical samples arrive at the laboratory is maximised at \(t = \frac{5}{3}\), according to the model. (3 marks)
Let the total number of medical samples that arrive at the laboratory between 8.00 am and 5.00 pm on a particular day be \(N\).
(b) An overestimate for the value of \(N\) can be calculated using three rectangles of equal width. These three rectangles, along with the graph of \(y=m(t)\) where \(0 \le t \le 9\), are shown in Figure 4.
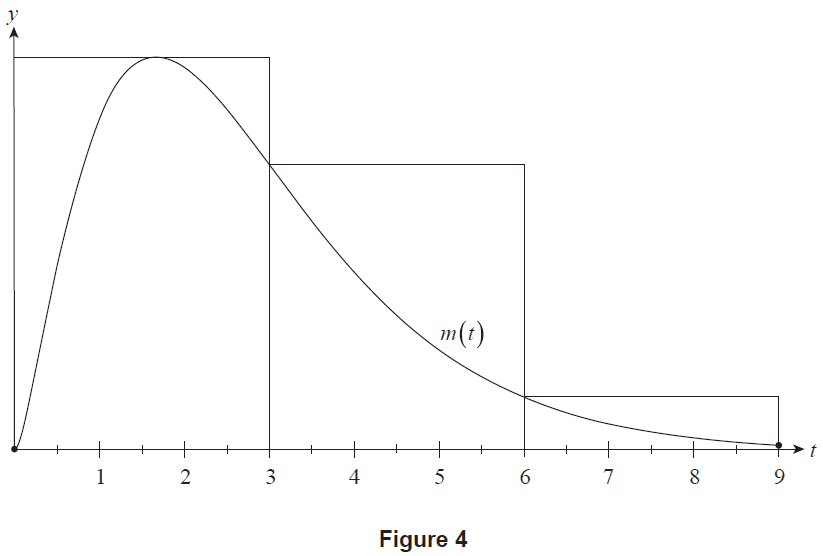
Figure 4
(i) Calculate the value of this overestimate. (2 marks)
(ii) If an overestimate of \(N\) was calculated using an increasing number of rectangles of equal width, it would approach the true value of \(N\). Calculate this value of \(N\), correct to the nearest integer. (1 mark)
When a medical sample arrives at the laboratory, it is placed in a queue before being processed. The medical samples are processed at a constant rate of 150 samples per hour. Let the function \(p(t)=150\) represent the rate at which medical samples are processed. Figure 5 shows the graphs of \(y=m(t)\) and \(y=p(t)\), where \(0 \le t \le 9\). The graphs of \(y=m(t)\) and \(y=p(t)\) intersect at \(t=0.670\) and \(t=3.36\) (correct to three significant figures).
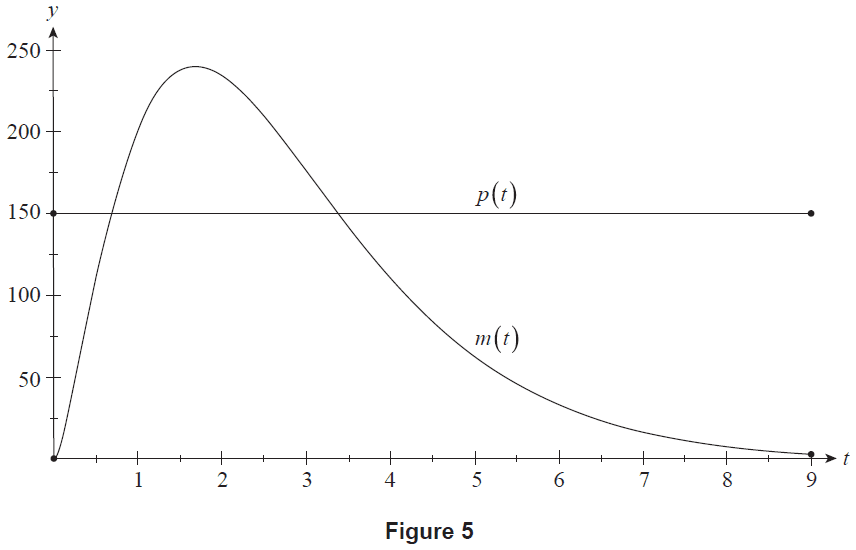
Figure 5
(c) At 8.00 am (\(t=0\)), the laboratory had 600 medical tests in the queue to be processed.
(i) Explain why the number of items in the queue is decreasing until 0.670 hours after 8.00 am. (1 mark)
(ii) During the time that the number of items in the queue was increasing, the queue increased by \(K\) medical samples.
(1) Write an integral expression that could be used to calculate \(K\). (2 marks)
(2) Hence, or otherwise, determine the value of \(K\), correct to the nearest integer. (1 mark)
(iii) Determine the number of medical samples in the queue at 5.00 pm. (2 marks)
The graph of \(y=x\ln x - x\) where \(x>0\) is shown in Figure 6.
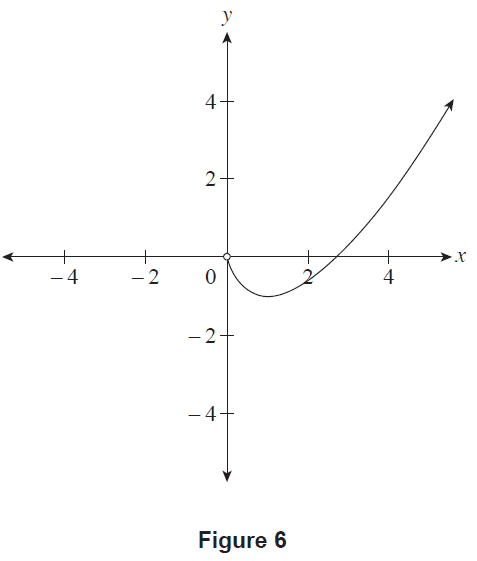
Figure 6
(a) (i) Show that \(\frac{dy}{dx} = \ln x\). (1 mark)
(ii) Hence, using an algebraic approach, determine the \(y\)-coordinate of the stationary point of \(y=x\ln x - x\). (2 marks)
Consider the family of functions of the form \(y = x\ln x - x + (\ln k)x\), where \(x>0\) and \(k\) is a positive constant. Each function in this family has a stationary point at \(A\), as shown in Figure 7.
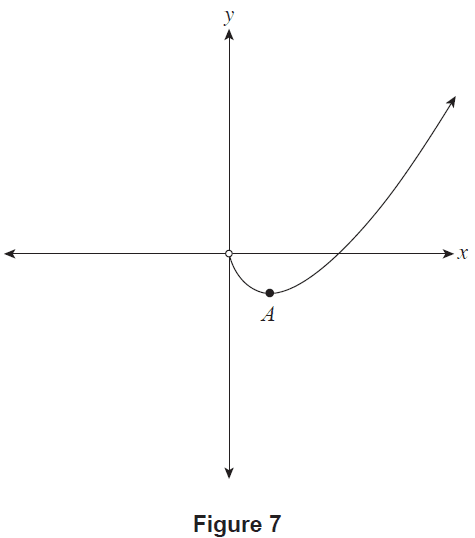
Figure 7
(b) Complete the table below by finding the \(y\)-coordinates of \(A\) for \(y = x\ln x - x + (\ln k)x\) where \(k=1, 2, 3,\) and \(4\). (1 mark)
| \(k\) | Function | \(y\)-coordinate of \(A\) |
|---|---|---|
| 1 | \(x\ln x - x\) | |
| 2 | \(x\ln x - x + (\ln 2)x\) | |
| 3 | \(x\ln x - x + (\ln 3)x\) | |
| 4 | \(x\ln x - x + (\ln 4)x\) |
(c) Hence, make a conjecture for the \(y\)-coordinate of \(A\), for any value of \(k\). (1 mark)
(d) Prove or disprove your conjecture. (4 marks)
A company produces a type of fruit-filled chocolate called Choc-pricots. They are produced on an automated assembly line that can result in imperfect Choc-pricots.

(a) The probability is 0.15 that a Choc-pricot randomly selected off the assembly line is imperfect. Use the binomial distribution to determine the probability that, in a random sample of 80 Choc-pricots:
(i) exactly 6 Choc-pricots will be imperfect. (1 mark)
(ii) more than 20 Choc-pricots will be imperfect. (2 marks)
The manager of the assembly line can adjust the rate of production of Choc-pricots, resulting in a change in the probability that a randomly selected Choc-pricot is imperfect. This probability can be modelled by the function \[ p(x) = \sin(0.00392x^2) + e^{-x}, \text{ for } 0 < x \le 20, \] where \(p(x)\) represents the probability that a randomly selected Choc-pricot is imperfect, and \(x\) represents the rate of production measured in Choc-pricots per second.
(b) On the axes in Figure 8, sketch the graph of \(y=p(x)\). (3 marks)
Figure 8
(c) Using the function \(p(x)\), determine the possible rate(s) of production that resulted in the given probability of 0.15 stated in part (a). (2 marks)
(d) The minimum probability that a randomly selected Choc-pricot is imperfect, according to the function \(p(x)\), is 0.0781 (correct to three significant figures). State the corresponding rate of production that would result in this probability. (1 mark)
(e) The manager chooses a new production rate for the assembly line. They claim that the production rate that they have chosen will result in the minimum probability that a randomly selected Choc-pricot is imperfect.
After running the assembly line at the new production rate for one day, a quality-control officer randomly selects 80 Choc-pricots and 6 are imperfect.
(i) Calculate \(\hat{p}\), the proportion of Choc-pricots that are imperfect in the sample of 80 Choc-pricots manufactured at the new production rate. (1 mark)
(ii) Assuming that a sample size of 80 is large enough for the central limit theorem to apply, determine a 90% confidence interval for the proportion of Choc-pricots that will be imperfect at the new production rate. (2 marks)
(iii) Using the confidence interval that you calculated in part (e)(ii), can it be concluded that the manager's claim is false with 90% confidence? Justify your answer. (2 marks)
(iv) Using the confidence interval that you calculated in part (e)(ii) and \(p(x)\), determine with 90% confidence the upper and lower bounds of the new production rate. (2 marks)
Let \(f(x) = \sqrt{8-x^3}\) for \(x < 2\).
(a) Show that \(f'(x) = \frac{-3x^2}{2\sqrt{8-x^3}}\) for \(x<2\). (1 mark)
The graph of \(y=f(x)\) is shown in Figure 9, along with the normal to the graph at \(x=-1\).
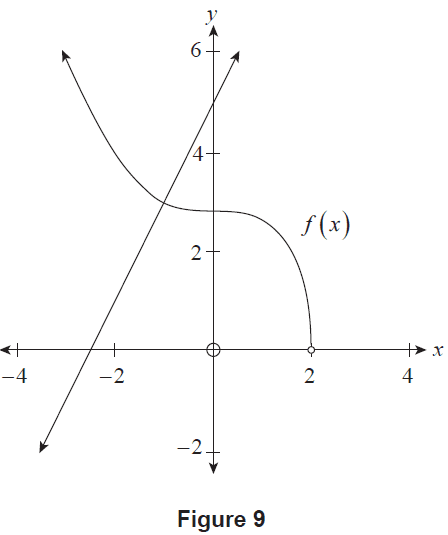
Figure 9
(b) (i) Show that the normal to the graph of \(y=f(x)\) at \(x=-1\) has the equation \(2x-y=-5\). (3 marks)
(ii) State the \(x\)-intercept of the normal \(2x-y=-5\). (1 mark)
(c) Consider the normal to the graph of \(y=f(x)\) at \(x=a\), where \(a < 2\).
(i) Show that the \(x\)-intercept of this normal is \(x = a - \frac{3}{2}a^2\). (4 marks)
(ii) Hence, using an algebraic approach, find the value of \(a\) such that the \(x\)-intercept of this normal is maximised. (2 marks)
The service life of an item is defined as an item's total life in use from the point of sale to the point of discard. A probability density function often used to model the service life of items is of the form \[ p_k(x) = \frac{k}{2} \left(\frac{x}{2}\right)^{k-1} e^{-\left(\frac{x}{2}\right)^k} \] where \(x\) is measured in years for \(x \ge 0\), and \(k\) is a constant such that \(k \ge 1\). The value of \(k\) is determined by the failure rate of the item over time.
(a) Consider the case where \(k=2\), resulting in the probability density function \[ p_2(x) = \frac{x}{2} e^{-\left(\frac{x}{2}\right)^2} \] The function \(p_2(x)\) can be used to model the service life of Product A.
(i) Using definite integrals, determine the probability that a randomly selected Product A will have a service life of 1.5 years or less. (1 mark)
(ii) An approximate measure of the anticipated service life for Product A is \(m\), the median service life of the item, which can be calculated using the equation: \[ \int_0^m p_2(x)dx = 0.5. \] Using your answer to part (a)(i), explain why the median service life of Product A is greater than 1.5 years. (1 mark)
(b) (i) If \(y = -e^{-\left(\frac{x}{2}\right)^k}\), show that \(\frac{dy}{dx} = \frac{k}{2}\left(\frac{x}{2}\right)^{k-1}e^{-\left(\frac{x}{2}\right)^k}\). (1 mark)
When calculating the median service life of an item, \(m\), using the probability density function \(p_k(x)\), the following equation can be used: \[ \int_0^m p_k(x) dx = 0.5. \]
(ii) Determine the exact value of \(k\) that would result in \(p_k(x)\) having a median service life of 1.5 years. (5 marks)
end of booklet
SACE is a registered trademark of the South Australian Certificate of Education. The SACE does not endorse or make any warranties regarding this study resource. Past SACE exams and related content can be accessed directly at www.sace.sa.edu.au.
