WACE Maths Methods ATAR Section 1 Topic Tests
Continuous Random Variables Topic Test 1
Section One: Technology-free
Number of marks: 15
Reading time: 1 minute
Writing time: 15 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
(a) The uniformly distributed continuous random variable \(X\) has an expected value of 6 and a maximum value of 9. Determine the variance of \(X\). (3 marks)
(b) The binomially distributed discrete random variable \(W\) has a mean of \(\frac{1}{2}\) and a variance of \(\frac{5}{12}\). Evaluate \(P(W = 1)\). (3 marks)
The heights reached by a species of small plant at maturity are measured by a team of biologists. The results are shown in the histogram of relative frequencies below.
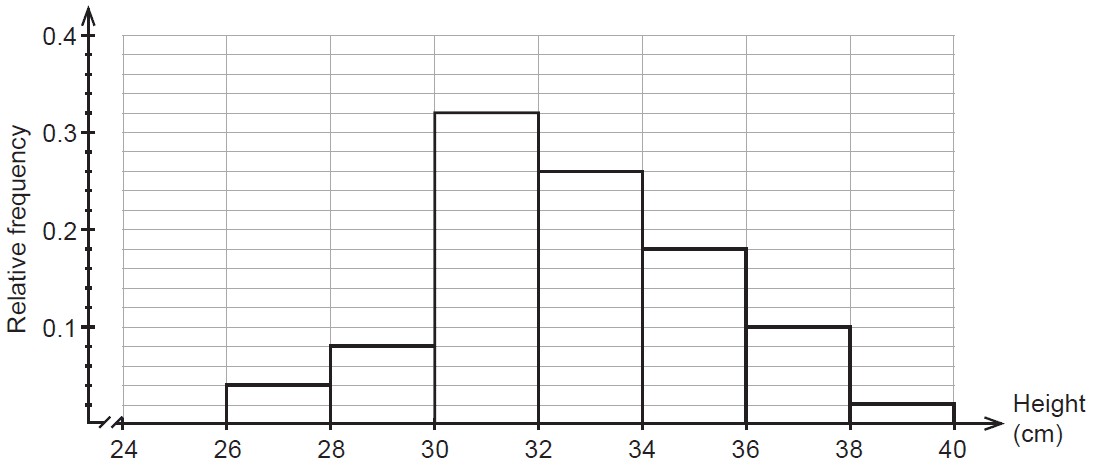
(a) Determine the probability that a mature plant of this species reaches no higher than 30 cm. (1 mark)
(b) If a mature plant reaches a height of at least 32 cm, what is the probability that its height reaches above 38 cm? (2 marks)
Another team of biologists is studying the mature heights of a species of hedge. The height, \(h\) metres, has a probability density function, \(d(h)\), as given below.
\[ d(h) = \begin{cases} \frac{h-1}{5} & \text{for } 1 \le h \le 2 \\ kh^2 & \text{for } 2 < h \le 4 \\ 0 & \text{otherwise} \end{cases} \](c) What percentage of hedges from this study reaches a mature height less than 2 m? (3 marks)
(d) Determine the value of \(k\). (3 marks)
End of questions
Continuous Random Variables Topic Test 2
Section One: Technology-free
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The table of values below may be used to assist you in answering part (b) of this question.
| \(\sin(0) = 0\) | \(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\) | \(\sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\) | \(\sin\left(\frac{\pi}{2}\right) = 1\) |
| \(\cos(0) = 1\) | \(\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\) | \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\) | \(\cos\left(\frac{\pi}{2}\right) = 0\) |
(a)
(i) Determine \( \frac{d}{dx} \left(x \sin\left(\frac{\pi x}{4}\right)\right) \). (2 marks)
(ii) Hence show that
\[ \int \frac{\pi x}{4} \cos\left(\frac{\pi x}{4}\right) dx = x \sin\left(\frac{\pi x}{4}\right) + \frac{4}{\pi} \cos\left(\frac{\pi x}{4}\right) + c \]
where \(c\) is a constant. (3 marks)
(b) The time in minutes, \(T\), between incoming phone calls at a call centre is a random variable with probability density function
\[ p(t) = \begin{cases} \frac{\pi}{4} \cos\left(\frac{\pi t}{4}\right) & 0 \le t \le 2 \\ 0, & \text{otherwise} \end{cases} \]
(i) Determine the probability that the time between two consecutive phone calls is less than 40 seconds. State your answer exactly. (3 marks)
(ii) Use the result from part (a)(ii) to determine the expected time between consecutive phone calls. (3 marks)
End of questions
Continuous Random Variables Topic Test 3
Section One: Technology-free
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The table of values below may be used to assist you in answering part (b) of this question.
| \(\sin(0) = 0\) | \(\sin\left(\frac{\pi}{6}\right) = \frac{1}{2}\) | \(\sin\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\sin\left(\frac{\pi}{3}\right) = \frac{\sqrt{3}}{2}\) | \(\sin\left(\frac{\pi}{2}\right) = 1\) |
| \(\cos(0) = 1\) | \(\cos\left(\frac{\pi}{6}\right) = \frac{\sqrt{3}}{2}\) | \(\cos\left(\frac{\pi}{4}\right) = \frac{\sqrt{2}}{2}\) | \(\cos\left(\frac{\pi}{3}\right) = \frac{1}{2}\) | \(\cos\left(\frac{\pi}{2}\right) = 0\) |
(a)
(i) Determine \( \frac{d}{dx} \left(x \sin\left(\frac{\pi x}{4}\right)\right) \). (2 marks)
(ii) Hence show that
\[ \int \frac{\pi x}{4} \cos\left(\frac{\pi x}{4}\right) dx = x \sin\left(\frac{\pi x}{4}\right) + \frac{4}{\pi} \cos\left(\frac{\pi x}{4}\right) + c \]
where \(c\) is a constant. (3 marks)
(b) The time in minutes, \(T\), between incoming phone calls at a call centre is a random variable with probability density function
\[ p(t) = \begin{cases} \frac{\pi}{4} \cos\left(\frac{\pi t}{4}\right) & 0 \le t \le 2 \\ 0, & \text{otherwise} \end{cases} \]
(i) Determine the probability that the time between two consecutive phone calls is less than 40 seconds. State your answer exactly. (3 marks)
(ii) Use the result from part (a)(ii) to determine the expected time between consecutive phone calls. (3 marks)
End of questions
Continuous Random Variables Topic Test 4
Section One: Technology-free
Number of marks: 11
Reading time: 1 minute
Writing time: 11 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Arnold would like to purchase a toy for his child's birthday. The Isosceles Toy Company claims that the number of weeks until delivery, \(X\), is a random variable whose probability density function is displayed in the graph below.
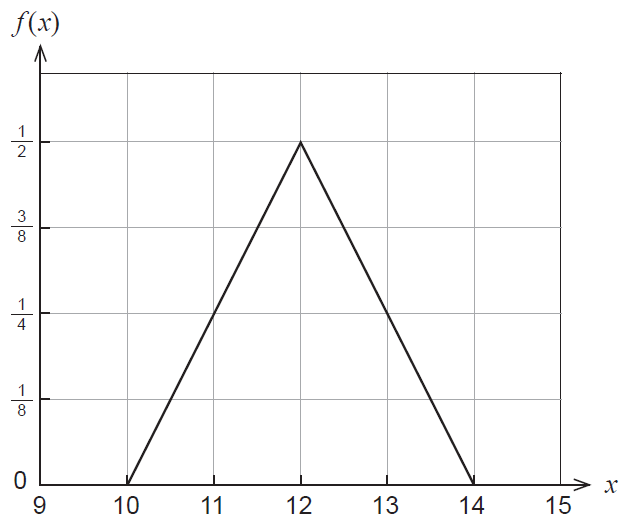
(a) What is the expected time for the toy to be delivered? (1 mark)
His child's birthday is 13 weeks away.
(b) What is the probability that the Isosceles Toy Company will deliver the toy in time for his child's birthday? (2 marks)
(c) Given that the toy arrives in time for his child's birthday, what is the probability that it arrives at least one week early? (2 marks)
Uniform Toys, a rival toy company, claims that the number of weeks until delivery of the same toy, \(Y\), is a random variable whose distribution is displayed in the graph below.
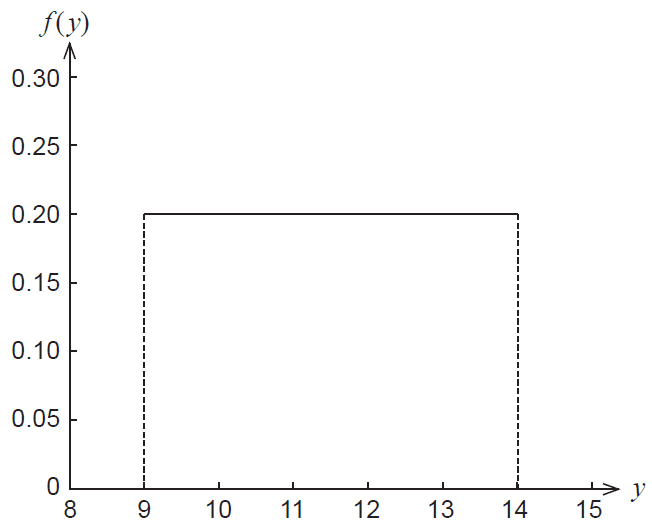
(d) Which toy company should Arnold choose if he would like to maximise the chance that the toy will be delivered in time for his child's birthday? Why? (2 marks)
Suppose that five people order the toy from Uniform Toys and let \(Z\) be a random variable that denotes the number of those people who receive the toy within 13 weeks.
(e) State the distribution for \(Z\). (2 marks)
(f) What is the probability that four out of the five people receive the toy within 13 weeks? (2 marks)
End of questions
Continuous Random Variables Topic Test 5
Section One: Technology-free
Number of marks: 10
Reading time: 1 minute
Writing time: 10 minutes
Section One:
Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
The error \(X\) in digitising a communication signal has a uniform distribution with probability density function given by
\[ f(x) = \begin{cases} 1, & -0.5 < x < 0.5, \\ 0, & \text{otherwise.} \end{cases} \](a) Sketch the graph of \(f(x)\). (2 marks)
(b) What is the probability that the error is at least 0.35? (1 mark)
(c) If the error is negative, what is the probability that it is less than -0.35? (2 marks)
(d) An engineer is more interested in the square of the error. What is the probability that the square of the error is less than 0.09? (2 marks)
(e) Calculate the variance of the error. (3 marks)
End of questions


