Question 1 (9 marks) [2018 Section 1 Q1]

A bag contains 1 red marble and 4 green marbles. A single marble is drawn from the bag. The random variable \(Y\) is defined as the number of green marbles drawn from the bag.

(a) Complete the probability distribution for \(Y\) shown below. (2 marks)

\(y\)	0	1
\(P(Y=y)\)

(b) State the distribution of \(Y\). (1 mark)

(c) Determine the mean and standard deviation of the distribution. (2 marks)

The above process is repeated five times, with the marble being replaced every time. The random variable \(X\) is defined as the number of green marbles drawn from the bag in five attempts.

(d) State the distribution of \(X\), including its parameters. (2 marks)

(e) Evaluate the probability of selecting exactly two green marbles. (2 marks)

Question 2 (6 marks) [2018 Section 1 Q2]

For a set of data values that are normally distributed, approximately 68% of the values will lie within one standard deviation of the mean, approximately 95% of the values will lie within two standard deviations of the mean and approximately 99.7% of the values will lie within three standard deviations of the mean.

If the heights of a large group of women are normally distributed with a mean \(\mu = 163\) cm and standard deviation \(\sigma = 7\) cm, use the above information to answer the following questions:

(a) A statistician says that almost all of the women have heights in the range 142 cm to 184 cm. Comment on her statement. (2 marks)

(b) Approximately what percentage of women in the group has a height greater than 170 cm? (2 marks)

(c) Approximately 2.5% of the women are shorter than what height? (2 marks)

Question 3 (12 marks) [2018 Section 1 Q3]

(a) Differentiate \((2x^3+1)^5\). (2 marks)

(b) Given \(g'(x) = e^{2x}\sin(3x)\), determine a simplified value for the rate of change of \(g'(x)\) when \(x=\frac{\pi}{2}\). (3 marks)

(c) Determine the following:

(i) \(\int 3\cos(2x) dx\). (2 marks)

(ii) \(\int_0^1 \frac{3x+1}{3x^2+2x+1} dx\). (3 marks)

(d) If \(f'(x) = e^{-2x}\), find the expression for \(y=f(x)\), given \(f(0)=-2\). (2 marks)

Question 4 (4 marks) [2018 Section 1 Q4]

Ten shop owners in a coastal resort were asked how many extra staff they intended to hire for the next holiday season. Their responses are shown below:

3, 0, 2, 1, 2, 1, 1, 0, 2, 1

If \(N\) = number of additional staff,

(a) complete the probability distribution of \(N\) below. (2 marks)

\(n\)	0	1	2	3
\(P(N=n)\)

(b) what is the mean number of staff the shop owners intend to hire? (2 marks)

Question 5 (3 marks) [2018 Section 1 Q5]

A 95% confidence interval for a population proportion based on a sample size of 200 has width \(w\). What sample size is required to obtain a 95% confidence interval of width \(\frac{w}{3}\)?

Question 6 (8 marks) [2018 Section 1 Q6]

A company manufactures and sells an item for $\(x\). The profit, $\(P\), made by the company per item sold is dependent on the selling price and can be modelled by the function:

\[ P(x) = \frac{50 \ln\left(\frac{x}{2}\right)}{x^2} \text{ where } 1.5 \le x \le 10 \]

The graph of \(P(x)\) is shown below:

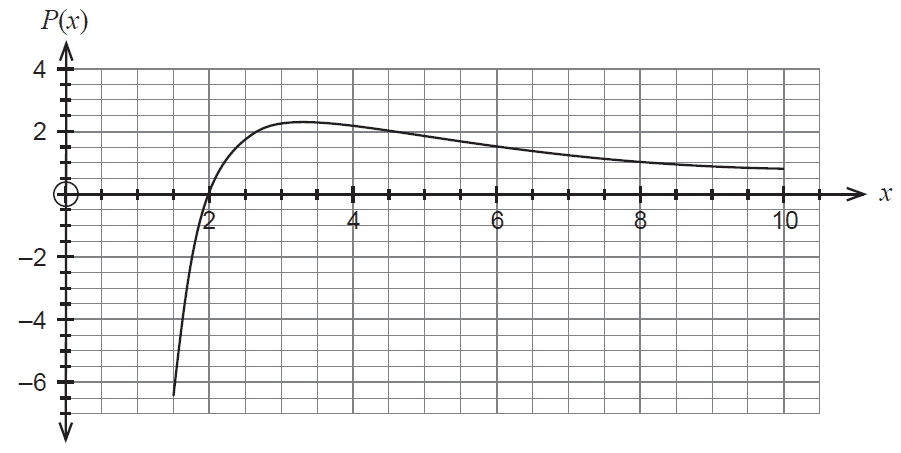
(a) Describe how the profit per item sold varies as the selling price changes. (3 marks)

(b) Determine the exact price that should be charged for the item if the company wishes to maximise the profit per item sold. (5 marks)

Question 7 (10 marks) [2018 Section 1 Q7]

(a) Determine a simplified expression for \(\frac{d}{dx}(x\ln(x))\). (2 marks)

(b) Use your answer from part (a) to show that \(\int \ln(x) dx = x\ln(x) - x + c\), where c is a constant. (4 marks)

The graphs of the functions \(f(x)=5\) and \(g(x)=\ln(x)\) are shown below.

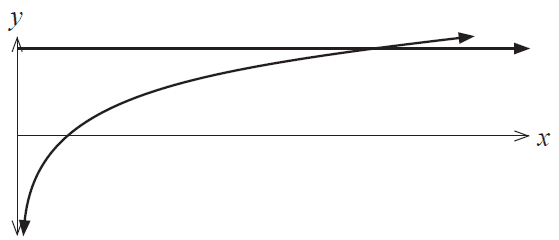
(c) Determine the exact area enclosed between the \(x\) axis, the \(y\) axis and the functions \(f(x)\) and \(g(x)\). (4 marks)

Question 8 (8 marks) [2018 Section 2 Q8]

Consider the function \(f(x) = \log_a(x-1)\) where \(a > 1\).

(a) On the axes below, sketch the graph of \(f(x)\), labelling important features. (3 marks)

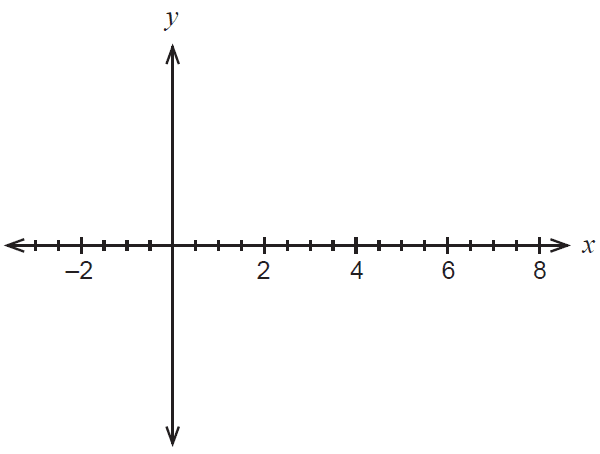
(b) Determine the value of \(m\) if \(f(m)=1\). (2 marks)

(c) Determine the coordinates of the \(x\)-intercept of \(f(x+b)+c\), where \(b\) and \(c\) are positive real constants. (3 marks)

Question 9 (8 marks) [2018 Section 2 Q9]

The concentration, \(C\), of a drug in the blood of a patient \(t\) hours after the initial dose can be modelled by the equation below.

\[ C = 4e^{-0.05t} \text{ mg/L} \]

Patients requiring this drug are said to be in crisis if the concentration of the drug in their blood falls below 2.5 mg/L.

A patient is given a dose of the drug at 9 am.

(a) What was the concentration in the patient's blood immediately following the initial dose? (1 mark)

(b) What is the concentration of the drug in the patient's blood at 11.30 am? (2 marks)

(c) Find the rate of change of \(C\) at 1 pm. (2 marks)

(d) What is the latest time the patient can receive another dose of the drug if they are to avoid being in crisis? (3 marks)

Question 10 (7 marks) [2018 Section 2 Q10]

The following function is a probability density function on the given interval:

\[ f(x) = \begin{cases} ax^2(x-2) & \text{for } 0 \le x \le 2 \\ 0 & \text{otherwise} \end{cases} \]

(a) Find the value of \(a\). (3 marks)

(b) Find the probability that \(x \ge 1.2\). (2 marks)

(c) Find the median of the distribution. (2 marks)

Question 11 (8 marks) [2018 Section 2 Q11]

Ava is flying a drone in a large open space at a constant height of 5 metres above the ground. She flies the drone due north so that it passes directly over her head and then, sometime later, reverses its direction and flies the drone due south so it passes directly over her again. With \(t=0\) defined as the moment when the drone first flies directly above Ava's head, the velocity of the drone, at time \(t\) seconds, is given by:

\[ v = 2 \sin\left(\frac{t}{3} + \frac{\pi}{6}\right) \text{ m/s } 0 \le t \le 16 \]

(a) Determine \(x(t)\), the displacement of the drone at \(t\) seconds, where \(x(0)=0\). (3 marks)

(b) Where is the drone in relation to the pilot after 16 seconds? (2 marks)

(c) At a particular time, the drone is heading due south and it is decelerating at 0.5 m/s². How far has the drone travelled from its initial position directly above Ava's head until this particular time? (3 marks)

Question 12 (19 marks) [2018 Section 2 Q12]

The manager of the mail distribution centre in an organisation estimates that the weight, \(x\) (kg), of parcels that are posted is normally distributed, with mean 3 kg and standard deviation 1 kg.

(a) What percentage of parcels weigh more than 3.7 kg? (2 marks)

(b) Twenty parcels are received for posting. What is the probability that at least half of them weigh more than 3.7 kg? (3 marks)

The cost of postage, ($) \(y\), depends on the weight of a parcel as follows:

• a cost of $5 for parcels 1 kg or less
• an additional variable cost of $1.50 for every kilogram or part thereof above 1 kg to a maximum of 4 kg
• a cost of $12 for parcels above 4 kg.

(c) Complete the probability distribution table for \(Y\). (4 marks)

\(x\)	\(\le 1\)	\(1 < x \le 2\)	\(2 < x \le 3\)	\(3 < x \le 4\)	\(x > 4\)
\(y\)	$5
\(P(Y=y)\)

(d) Calculate the mean cost of postage per parcel. (2 marks)

(e) Calculate the standard deviation of the cost of postage per parcel. (3 marks)

(f) If the cost of postage is increased by 20% and a surcharge of $1 is added for all parcels, what will be the mean and standard deviation of the new cost? (3 marks)

(g) Show one reason why the given normal distribution is not a good model for the weight of the parcels. (2 marks)

Question 13 (10 marks) [2018 Section 2 Q13]

The proportion of caravans on the road being towed by vehicles that have the incorrect towing capacity is \(p\).

(a) Show, using calculus, that to maximise the margin of error a value of \(\hat{p} = 0.5\) should be used. Note: As \(z\) and \(n\) are constants, the standard error formula can be reduced to \(E = \sqrt{\hat{p}(1-\hat{p})}\). (3 marks)

(b) A consulting firm wants to determine \(p\) within 8% with 99% confidence. How many towing vehicles should be tested at a random check? (3 marks)

(c) Six months later, the consulting firm carries out a random sampling of towing vehicles. A 99% confidence interval calculated for the proportion of vehicles with incorrect towing capacity is (0.342, 0.558). Determine the number of vehicles in the sample that have an incorrect towing capacity. (4 marks)

Question 14 (5 marks) [2018 Section 2 Q14]

(a) The table below examines the values of \( \frac{a^h-1}{h} \) for various values of \(a\) as \(h\) approaches zero. Complete the table, rounding your values to five decimal places. (2 marks)

\(h\)	\(a=2.60\)	\(a=2.70\)	\(a=2.72\)	\(a=2.80\)
0.1	1.00265		1.05241	1.08449
0.001	0.95597	0.99375
0.00001	0.95552			1.02962

It can be shown that \(\frac{d}{dx}(a^x) = a^x \lim_{h \to 0}\left(\frac{a^h-1}{h}\right)\).

(b) What is the exact value of \(a\) for which \(\frac{d}{dx}(a^x) = a^x\)? Explain how the above definition and the table in part (a) support your answer. (3 marks)

Question 15 (5 marks) [2018 Section 2 Q15]

The population of mosquitos, \(P\) (in thousands), in an artificial lake in a housing estate is measured at the beginning of the year. The population after \(t\) months is given by the function, \(P(t) = t^3 + at^2 + bt + 2, 0 \le t \le 12\).

The rate of growth of the population is initially increasing. It then slows to be momentarily stationary in mid-winter (at \(t=6\)), then continues to increase again in the last half of the year.

Determine the values of \(a\) and \(b\).

Question 16 (8 marks) [2018 Section 2 Q16]

Let \(f(x)\) be a function such that \(f(-2)=4, f(-1)=0, f(0)=-1, f(1)=0\) and \(f(3)=2\). Further, \(f'(x)<0\) for \(-2 \le x < 0\), \(f'(0)=0\) and \(f'(x)>0\) for \(0 < x \le 3\).

(a) Evaluate the following definite integrals:

(i) \(\int_{-1}^3 f'(x) dx\). (2 marks)

(ii) \(\int_{-2}^3 f'(x) dx\). (2 marks)

(b) What is the area bounded by the graph of \(f'(x)\) and the \(x\) axis between \(x=-2\) and \(x=3\)? Justify your answer. (4 marks)

Question 17 (14 marks) [2018 Section 2 Q17]

Tina believes that approximately 60% of the mangoes she produces on her farm are large. She takes a random sample of 500 mangoes from a day's picking.

(a) Assuming Tina is correct and 60% of the mangoes her farm produces are large, what is the approximate probability distribution of the sample proportion of large mangoes in her sample? (3 marks)

(b) What is the probability that the sample proportion of large mangoes is less than 0.58? (2 marks)

(c) Tina decides to select the mangoes for her sample as they pass along the conveyor belt to be sorted. Describe briefly how Tina should select her sample. (2 marks)

A random sample of 500 contains 250 large mangoes.

(d) On the basis of this data, estimate the proportion of large mangoes produced on the farm. (1 mark)

(e) Calculate a 95% confidence interval for the proportion of large mangoes produced on the farm, rounded to four decimal places. (3 marks)

(f) On the basis of your calculations, how would you respond to Tina's belief that the proportion of large mangoes produced is at least 60%? Justify your response. (2 marks)

(g) What can Tina do to further test her belief? (1 mark)

Question 18 (7 marks) [2018 Section 2 Q18]

The ear has the remarkable ability to handle an enormous range of sound levels. In order to express levels of sound meaningfully in numbers that are more manageable, a logarithmic scale is used, rather than a linear scale. This scale is the decibel (dB) scale.

The sound intensity level, \(L\), is given by the formula below:

\[ L = 10 \log_{10}\left(\frac{I}{I_0}\right) \text{ dB where } I \text{ is the sound intensity and } I_0 \text{ is the reference sound intensity.} \]

\(I\) and \(I_0\) are measured in watt/m².

(a) Listening to a sound intensity of 5 billion times that of the reference intensity (\(I=5\times 10^9 I_0\)) for more than 30 minutes is considered unsafe. To what sound intensity level does this correspond? (2 marks)

(b) The reference sound intensity, \(I_0\), has a sound intensity level of 0 dB. If a household vacuum cleaner has a sound intensity \(I = 1 \times 10^{-5}\) watt/m² and this corresponds to a sound intensity level \(L=70\) dB, determine \(I_0\). (2 marks)

The average sound intensity level for rainfall is 50 dB and for heavy traffic 85 dB.

(c) How many times more intense is the sound of traffic than that of rainfall? (3 marks)