2024 WACE Maths Methods ATAR Exam Section 1
ATAR course examination. Section One: Calculator-free
This is a full SCSA WACE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official WACE exams split into short tests you can do anytime.
Number of marks: 51
Reading time: 5 minutes
Writing time: 50 minutes
Section One: Calculator-free (51 Marks)
This section has seven questions. Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Working time: 50 minutes.
(a) Differentiate the function \(f(x) = x^2 \ln(4x + 3)\). (2 marks)
(b) Determine a fully simplified expression for \(g(x)\), given that \(g'(x) = \frac{3x}{3x^2 + 1}\) and \(g(1) = \ln(6)\). (4 marks)
An advertising graphic moves across the bottom of a television screen during a sporting game, changing direction to attract viewer attention. The position of the graphic is modelled by \[x(t) = \frac{1}{3}t^3 - 7t^2 + 40t\] where \(x\), in centimetres, is the position of the graphic relative to the left side of the screen, and \(t\), in seconds, is the time from when the graphic first appears on the screen.
The position of the graphic at integer time increments is given in the table below.
| \(\boldsymbol{t}\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(\boldsymbol{x(t)}\) | \(0\) | \(33\frac{1}{3}\) | \(54\frac{2}{3}\) | \(66\) | \(69\frac{1}{3}\) | \(66\frac{2}{3}\) | \(60\) | \(51\frac{1}{3}\) |
| \(\boldsymbol{t}\) | \(8\) | \(9\) | \(10\) | \(11\) | \(12\) | \(13\) | \(14\) | \(15\) |
| \(\boldsymbol{x(t)}\) | \(42\frac{2}{3}\) | \(36\) | \(33\frac{1}{3}\) | \(36\frac{2}{3}\) | \(48\) | \(69\frac{1}{3}\) | \(102\frac{2}{3}\) | \(150\) |
(a) Determine the velocity of the graphic when it first appears on the screen. (2 marks)
(b) Is the graphic initially speeding up or slowing down? Justify your answer. (2 marks)
(c) Evaluate \(\int_3^9 v(t)dt\) and explain what this integral represents. (3 marks)
(d) Calculate the total distance travelled by the graphic from the time it enters the screen to the time it leaves the screen 15 seconds later. (3 marks)
The tables below display the partially completed probability distribution and cumulative distribution for a discrete random variable \(X\).
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X=x)}\) | \(0.2\) | \(0.15\) | \(0.05\) |
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X \le x)}\) | \(0.2\) | \(0.6\) | \(0.95\) |
(a) Complete the missing probability entries in each of the tables above. (2 marks)
(b) Evaluate \(P(2 \le X \le 4)\). (2 marks)
(c) Evaluate \(P(X = 1 | X \le 3)\). (2 marks)
(a) The uniformly distributed continuous random variable \(X\) has an expected value of 6 and a maximum value of 9. Determine the variance of \(X\). (3 marks)
(b) The binomially distributed discrete random variable \(W\) has a mean of \(\frac{1}{2}\) and a variance of \(\frac{5}{12}\). Evaluate \(P(W = 1)\). (3 marks)
The function \(f(x) = \log_a(x)\) is plotted below, where \(a\) and \(p\) are constants.
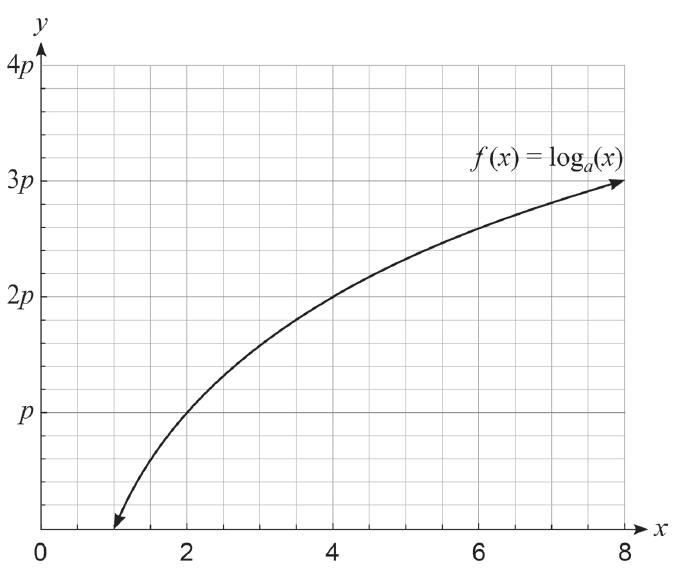
(a) Express \(\log_a(0.5)\) in terms of \(p\). (2 marks)
(b) Evaluate \(a^{5p}\). (2 marks)
(c) Solve \(\log_a(x-3) = 3p\) for \(x\). (2 marks)
The function \(f(x) = \log_a(x)\) has been transformed to give two other logarithmic functions with base \(a\) on the axes as shown below.
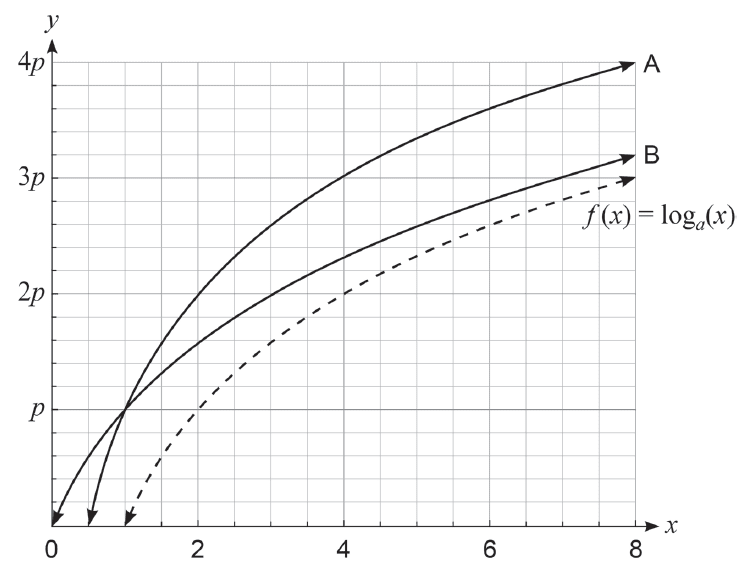
(d) Determine an equation for each of the two functions, A and B. (2 marks)
The graph of \(y = x \sin(\pi x)\) for \(0 \le x \le 1\) is shown below.
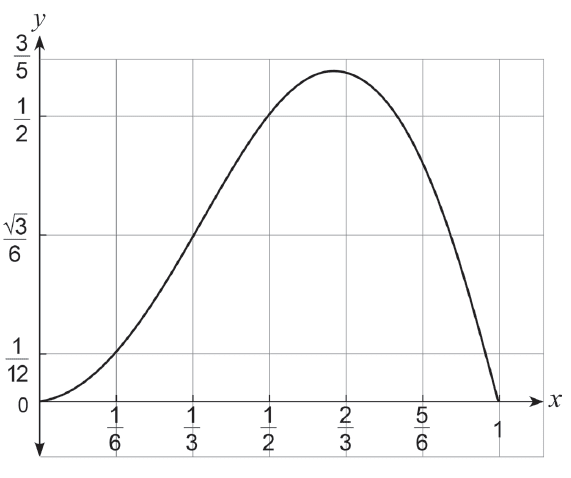
(a) On the diagram above, shade a region whose area is equal to \(\int_{1/6}^{1/2} x \sin(\pi x) dx\). (1 mark)
A spare diagram is provided at the end of this Question/Answer booklet. If you need to use it, cross out this attempt and indicate that you have redrawn it on the spare diagram.
(b)
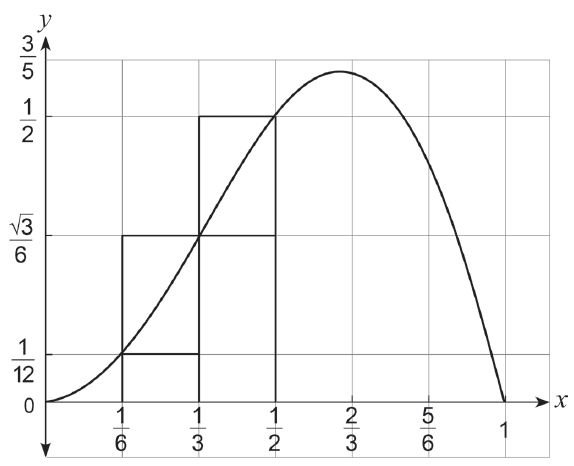
(i) By considering the areas of the rectangles shown in the graph of \(y = x \sin(\pi x)\) above, demonstrate and explain why \[\frac{1 + 2\sqrt{3}}{72} < \int_{1/6}^{1/2} x \sin(\pi x) dx < \frac{3 + \sqrt{3}}{36}\] (3 marks)
(ii) State one suggestion as to how the approximation from part (b)(i) could be improved. (1 mark)
A bicycle rolls down a ramp from an initial height of 5.15 m as shown in the diagram below.
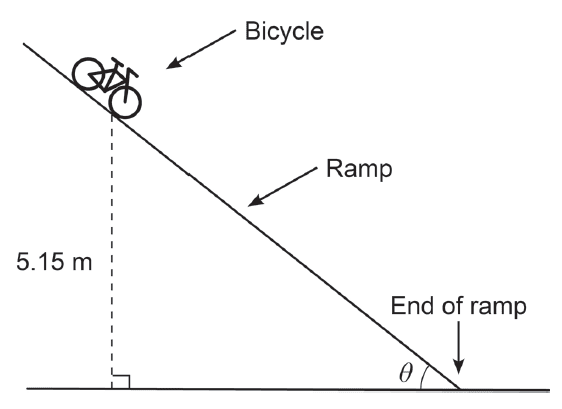
The speed, \(s\), of the bicycle (in metres per second) when it reaches the end of the ramp is given by \[s(\theta) = \sqrt{\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}}\] where \(\theta\) (in radians) is the ramp angle shown in the diagram.
(a) Determine the speed of the bicycle at the end of the ramp, if the ramp angle is 45°. (2 marks)
(b) Determine \(\frac{d}{d\theta}\left(\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}\right)\). Simplify your answer. (3 marks)
(c) Hence, show that \(\frac{ds}{d\theta} = \frac{1}{2\sin^2(\theta)} \frac{\sin(\theta)}{\sqrt{101\sin(\theta)-\cos(\theta)}}\). (2 marks)
(d) Use the increments formula to estimate the change in \(s\) if the ramp angle is changed from 45° to 46°. (3 marks)
END OF PAPER
2024 WACE Maths Methods ATAR Exam Section 2
ATAR course examination. Section Two: Calculator-assumed
This is a full SCSA WACE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official WACE exams split into short tests you can do anytime.
Number of marks: 100
Reading time: 10 minutes
Writing time: 100 minutes
Section Two: Calculator-assumed (100 Marks)
This section has ten questions. Answer all questions. Write your answers in the spaces provided.
Supplementary pages for planning/continuing your answers to questions are provided at the end of this Question/Answer booklet. If you use these pages to continue an answer, indicate at the original answer where the answer is continued, i.e. give the page number.
Working time: 100 minutes.
(a) Differentiate the function \(f(x) = x^2 \ln(4x + 3)\). (2 marks)
(b) Determine a fully simplified expression for \(g(x)\), given that \(g'(x) = \frac{3x}{3x^2 + 1}\) and \(g(1) = \ln(6)\). (4 marks)
An advertising graphic moves across the bottom of a television screen during a sporting game, changing direction to attract viewer attention. The position of the graphic is modelled by \[x(t) = \frac{1}{3}t^3 - 7t^2 + 40t\] where \(x\), in centimetres, is the position of the graphic relative to the left side of the screen, and \(t\), in seconds, is the time from when the graphic first appears on the screen.
The position of the graphic at integer time increments is given in the table below.
| \(\boldsymbol{t}\) | \(0\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) | \(6\) | \(7\) |
| \(\boldsymbol{x(t)}\) | \(0\) | \(33\frac{1}{3}\) | \(54\frac{2}{3}\) | \(66\) | \(69\frac{1}{3}\) | \(66\frac{2}{3}\) | \(60\) | \(51\frac{1}{3}\) |
| \(\boldsymbol{t}\) | \(8\) | \(9\) | \(10\) | \(11\) | \(12\) | \(13\) | \(14\) | \(15\) |
| \(\boldsymbol{x(t)}\) | \(42\frac{2}{3}\) | \(36\) | \(33\frac{1}{3}\) | \(36\frac{2}{3}\) | \(48\) | \(69\frac{1}{3}\) | \(102\frac{2}{3}\) | \(150\) |
(a) Determine the velocity of the graphic when it first appears on the screen. (2 marks)
(b) Is the graphic initially speeding up or slowing down? Justify your answer. (2 marks)
(c) Evaluate \(\int_3^9 v(t)dt\) and explain what this integral represents. (3 marks)
(d) Calculate the total distance travelled by the graphic from the time it enters the screen to the time it leaves the screen 15 seconds later. (3 marks)
The tables below display the partially completed probability distribution and cumulative distribution for a discrete random variable \(X\).
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X=x)}\) | \(0.2\) | \(0.15\) | \(0.05\) |
| \(\boldsymbol{x}\) | \(1\) | \(2\) | \(3\) | \(4\) | \(5\) |
| \(\boldsymbol{P(X \le x)}\) | \(0.2\) | \(0.6\) | \(0.95\) |
(a) Complete the missing probability entries in each of the tables above. (2 marks)
(b) Evaluate \(P(2 \le X \le 4)\). (2 marks)
(c) Evaluate \(P(X = 1 | X \le 3)\). (2 marks)
(a) The uniformly distributed continuous random variable \(X\) has an expected value of 6 and a maximum value of 9. Determine the variance of \(X\). (3 marks)
(b) The binomially distributed discrete random variable \(W\) has a mean of \(\frac{1}{2}\) and a variance of \(\frac{5}{12}\). Evaluate \(P(W = 1)\). (3 marks)
The function \(f(x) = \log_a(x)\) is plotted below, where \(a\) and \(p\) are constants.

(a) Express \(\log_a(0.5)\) in terms of \(p\). (2 marks)
(b) Evaluate \(a^{5p}\). (2 marks)
(c) Solve \(\log_a(x-3) = 3p\) for \(x\). (2 marks)
The function \(f(x) = \log_a(x)\) has been transformed to give two other logarithmic functions with base \(a\) on the axes as shown below.

(d) Determine an equation for each of the two functions, A and B. (2 marks)
The graph of \(y = x \sin(\pi x)\) for \(0 \le x \le 1\) is shown below.

(a) On the diagram above, shade a region whose area is equal to \(\int_{1/6}^{1/2} x \sin(\pi x) dx\). (1 mark)
A spare diagram is provided at the end of this Question/Answer booklet. If you need to use it, cross out this attempt and indicate that you have redrawn it on the spare diagram.
(b)

(i) By considering the areas of the rectangles shown in the graph of \(y = x \sin(\pi x)\) above, demonstrate and explain why \[\frac{1 + 2\sqrt{3}}{72} < \int_{1/6}^{1/2} x \sin(\pi x) dx < \frac{3 + \sqrt{3}}{36}\] (3 marks)
(ii) State one suggestion as to how the approximation from part (b)(i) could be improved. (1 mark)
A bicycle rolls down a ramp from an initial height of 5.15 m as shown in the diagram below.

The speed, \(s\), of the bicycle (in metres per second) when it reaches the end of the ramp is given by \[s(\theta) = \sqrt{\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}}\] where \(\theta\) (in radians) is the ramp angle shown in the diagram.
(a) Determine the speed of the bicycle at the end of the ramp, if the ramp angle is 45°. (2 marks)
(b) Determine \(\frac{d}{d\theta}\left(\frac{101 \sin(\theta) - \cos(\theta)}{\sin(\theta)}\right)\). Simplify your answer. (3 marks)
(c) Hence, show that \(\frac{ds}{d\theta} = \frac{1}{2\sin^2(\theta)} \frac{\sin(\theta)}{\sqrt{101\sin(\theta)-\cos(\theta)}}\). (2 marks)
(d) Use the increments formula to estimate the change in \(s\) if the ramp angle is changed from 45° to 46°. (3 marks)
END OF PAPER
WACE is a registered trademark of the School Curriculums and Standards Authority. The SCSA does not endorse or make any warranties regarding this study resource. Past WACE exams and related content can be accessed directly at www.senior-secondary.scsa.wa.edu.au


