QCAA Continuous Random Variables Mini Test 1
External Assessment Paper 2 — Technology-active
Number of marks: 12
Perusal time: 1 minute
Writing time: 18 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
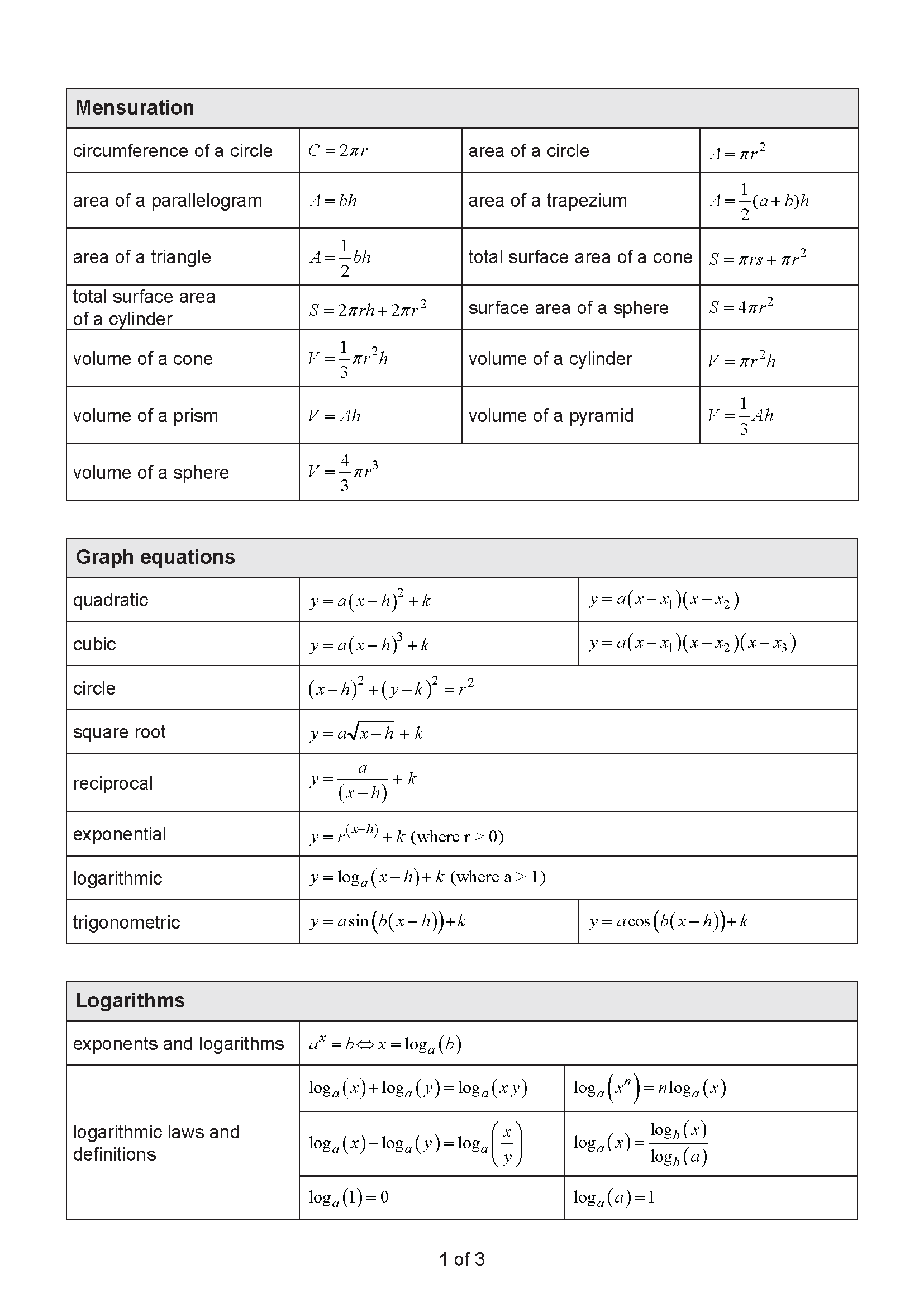
The normal distribution probability density function is \[ p(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \] with the parameters mean, \(\mu\), and standard deviation, \(\sigma\).
The speeds of electric scooter (e-scooter) riders on a particular section of a bike path are approximately normally distributed with a mean of 18 km/h. It is known that \(p(10) = 0.0135\).
The speed limit for e-scooters on this section of bike path is 23 km/h.
A speed camera is set up and records the speeds of 75 e-scooter riders. Every rider travelling faster than the speed limit is given a $143 fine. Before setting up the speed camera, the following suggestion was made.
Evaluate the reasonableness of this suggestion.
A random variable \(X\), defined over the interval \(a \le x \le b\), is uniformly distributed if its probability density function is defined by: \[ f(x) = \begin{cases} \frac{1}{b-a}, & a \le x \le b \\ 0, & \text{otherwise} \end{cases} \]
The expected value and variance of a uniform random variable \(X\) are \[ E(X) = \frac{(a+b)}{2} \quad \text{Var}(X) = \frac{(b-a)^2}{12} \]
A manufacturer has observed that the time that elapses between placing an order with a supplier and the delivery of the order is uniformly distributed between 100 and 180 minutes.
Determine the probability that the time between placing an order and delivery of the order will be within one standard deviation of the expected time.
END OF PAPER