2021 QCE Maths Methods Paper 1 Mini Test 2
External Assessment Paper 1 — Technology-free
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
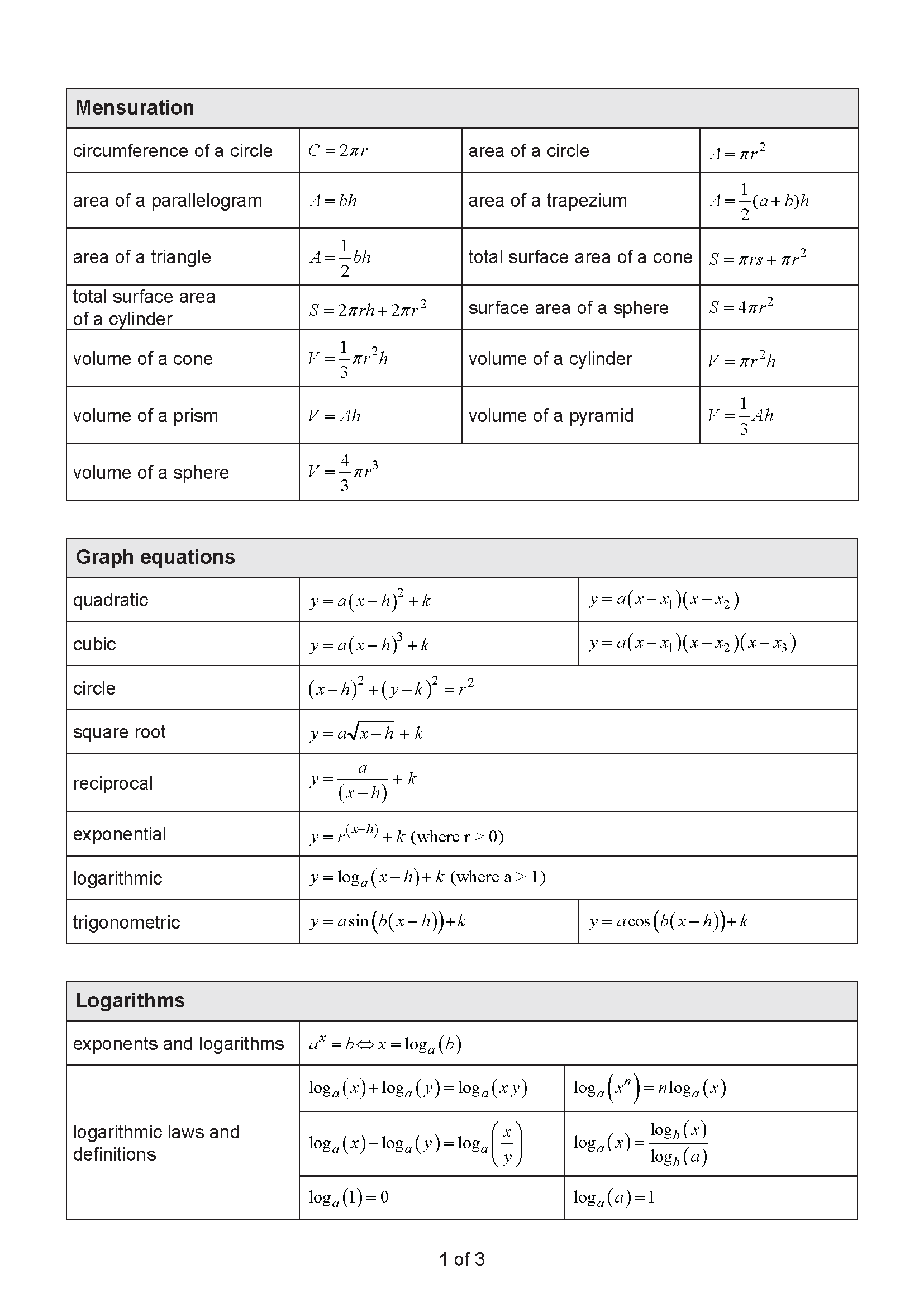
Determine the derivative with respect to \(x\) of the following functions.
a) \(y = (e^x + 1)^3\) [2 marks]
b) \(y = \frac{\sin(x)}{x^2}\) (Give your answer in simplest form.) [3 marks]
Consider the function \(f(x) = \ln(3x+4)\), for \(x > \frac{-4}{3}\).
a) Determine \(f'(x)\). [1 mark]
b) Determine the \(x\)-intercept of the graph of \(f(x)\). [2 marks]
c) Determine the gradient of the tangent to the graph of \(f(x)\) at the \(x\)-intercept. [1 mark]
END OF PAPER