2022 QCE Maths Methods Paper 2 Mini Test 6
External Assessment Paper 2 — Technology-active
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
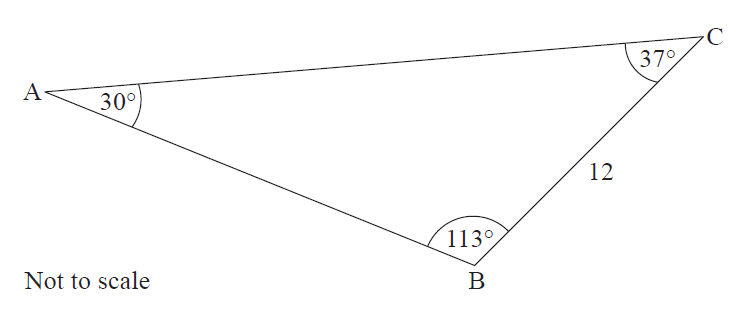
Determine the length of side AB in triangle ABC.
- (A) 22.13
- (B) 14.44
- (C) 9.97
- (D) 7.82
The solution of \(e^{2x-3} = 42\) is
- (A) 1.48
- (B) 2.31
- (C) 3.37
- (D) 4.54
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A snail is travelling along a straight path from point \(A\). The snail's velocity (cm min\(^{-1}\)) is modelled by \(v(t) = 1.4 \ln(1 + t^2)\), where \(t\) is time (in minutes) for \(0 \le t \le 15\).
An ant passes point \(A\) 12 minutes after the snail and follows the snail's path. The ant moves with a constant acceleration of 2 cm min\(^{-2}\) and passes the snail at \(t = 15\) minutes.
Determine the ant's velocity at point \(A\).
The intelligence quotient (IQ) of individuals in a population is normally distributed, with a mean of 100 and a standard deviation of 16.
Nine individuals are chosen at random from the population.
Determine the probability that no more than two of the individuals have an IQ of at least 120.
END OF PAPER