2024 QCE Maths Methods Paper 1 Mini Test 6
External Assessment Paper 1 — Technology-free
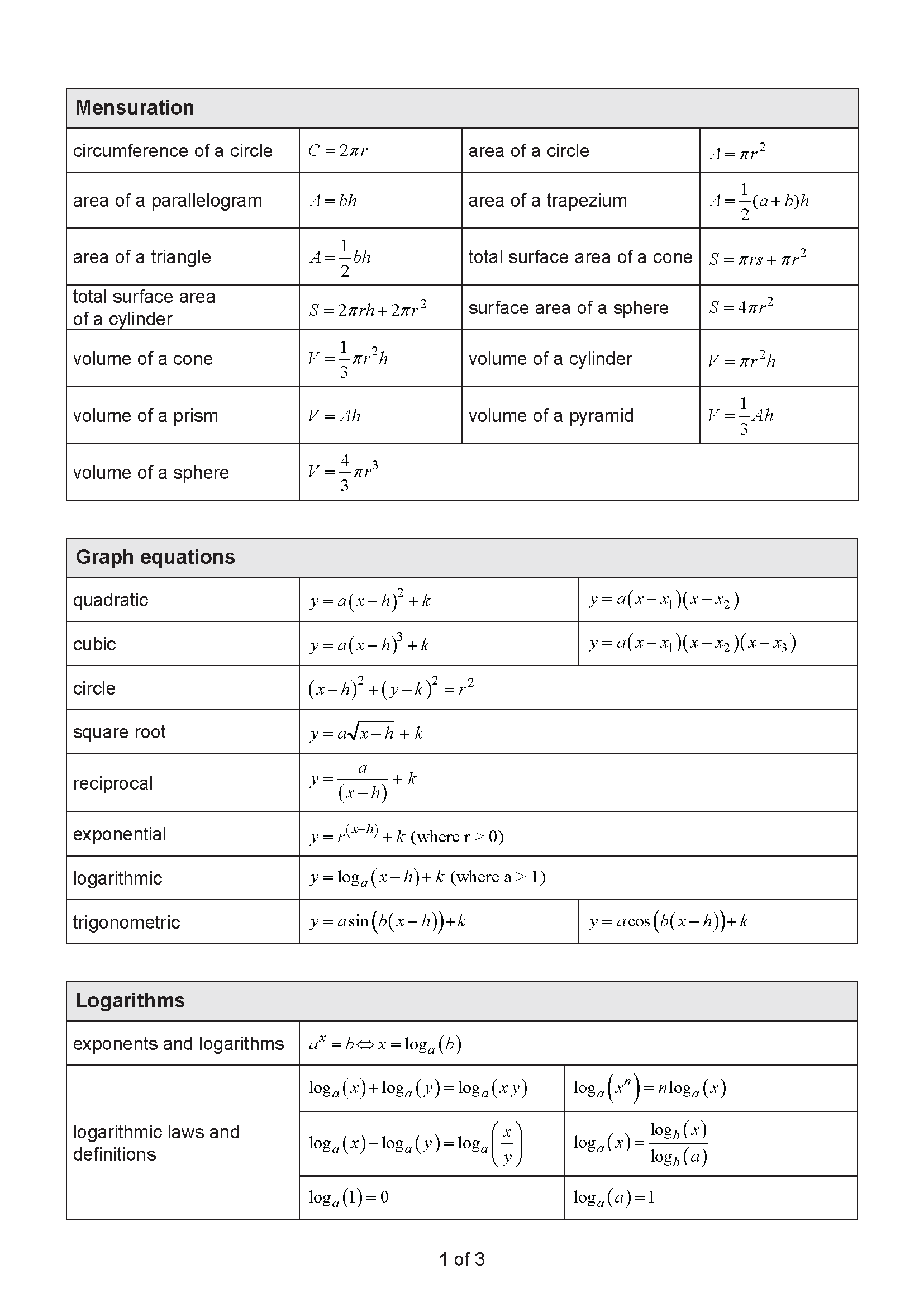
Number of marks: 9
Perusal time: 1 minute
Writing time: 15 minutes
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
A community group that uses social media created a new post on the internet on a day when they had 1000 members. The rate of change in their number of members (members/day) is given by \(f'(t) = 3e^{0.5t}\), where \(t\) represents days after the new post.
Determine the time it will take for the community group to achieve seven times the initial number of members. Express your answer in the form \(a\ln(b)\).
A permanent ice glacier is in a valley in New Zealand.
Due to the temperature changes of the seasons each year, the glacier expands for six months and recedes for six months. The changing distance of a point on the front edge of the glacier to a car park can be modelled by a sine function.
During the colder months, when the glacier expands, the front edge of the glacier moves to within 270 m of the car park. However, in the warmer months, when the glacier recedes, the front edge moves to a maximum distance of 280 m away from the car park.
The erosion effects of the glacier on the ground are of most interest to geologists when the absolute value of the acceleration of the front edge is greater than \(\frac{5\pi^2\sqrt{3}}{72}\) metres/month\(^2\). During these times, a team of geologists sets up a camp site nearby to perform field work. Whenever the acceleration is less than this, the geologists leave camp.
The following claim is made.
The geologists will spend a total of between seven and eight months at the camp site each calendar year.
Evaluate the reasonableness of this claim.
END OF PAPER