QCAA Maths Methods 2020 Exam 1 with solutions
Number of marks: 60
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
The graphs of \(f(x) = e^x\) and \(g(x) = x^2 - 1\) are shown.
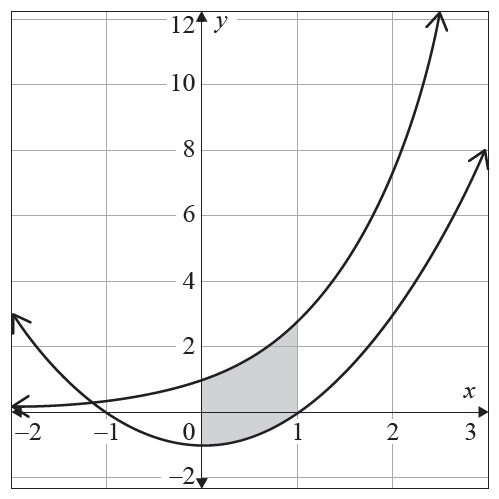
The area of the shaded section bounded by these graphs between the lines \(x = 0\) and \(x = 1\) is
- (A) \(1-e\)
- (B) \(e-2\)
- (C) \(e - \frac{5}{3}\)
- (D) \(e - \frac{1}{3}\)
Determine \(\int \frac{e^x+1}{e^x}dx\)
- (A) \(x - e^{-x} + c\)
- (B) \(x + e^{-x} + c\)
- (C) \(1 + xe^{-x} + c\)
- (D) \(x + xe^{-x} + c\)
Determine \(2 \int (4x + 6)^3 dx\)
- (A) \(16(4x+6)^4 + c\)
- (B) \(8(4x+6)^4 + c\)
- (C) \(\frac{(4x+6)^4}{2} + c\)
- (D) \(\frac{(4x+6)^4}{8} + c\)
Pulse rates of adult men are approximately normally distributed with a mean of 70 and a standard deviation of 8. Which of the following choices correctly describes how to determine the proportion of men that have a pulse rate greater than 78?
- (A) Determine the area to the left of \(z = 1\) under the standard normal curve.
- (B) Determine the area to the right of \(z = 1\) under the standard normal curve.
- (C) Determine the area to the right of \(z = -1\) under the standard normal curve.
- (D) Determine the area between \(z = -1\) and \(z = 1\) under the standard normal curve.
The equation of the tangent to the curve \(f(t) = te^t\) at \(t = 1\) is
- (A) \(y = et\)
- (B) \(y = 2et - e\)
- (C) \(y = et - e^2 + 1\)
- (D) \(y = 2et - 2e^2 + 1\)
If the probability of success in a Bernoulli trial is 0.30, the variance is
- (A) 0.70
- (B) 0.46
- (C) 0.30
- (D) 0.21
The life expectancy (in years) of an electronic component can be represented by the probability density function
\[ p(x) = \begin{cases} \frac{1}{x^2}, & x \ge 1 \\ 0, & \text{otherwise} \end{cases} \]The probability that the component lasts between 1 and 10 years is
- (A) 0.010
- (B) 0.100
- (C) 0.900
- (D) 0.990
A test includes six multiple choice questions. Each question has four options for the answer. If the answers are guessed, the probability of getting at most two questions correct is represented by
- (A) \(\binom{6}{0}0.25^0 \times 0.75^6 + \binom{6}{1}0.25^1 \times 0.75^5\)
- (B) \(\binom{6}{0}0.25^0 \times 0.75^6 + \binom{6}{1}0.25^1 \times 0.75^5 + \binom{6}{2}0.25^2 \times 0.75^4\)
- (C) \(1 - \left( \binom{6}{0}0.25^0 \times 0.75^6 + \binom{6}{1}0.25^1 \times 0.75^5 \right)\)
- (D) \(1 - \left( \binom{6}{0}0.25^0 \times 0.75^6 + \binom{6}{1}0.25^1 \times 0.75^5 + \binom{6}{2}0.25^2 \times 0.75^4 \right)\)
Determine \(\int \frac{x+1}{x^2 + 2x} dx\)
- (A) \(\ln \left( \frac{1}{2x+2} \right) + c\)
- (B) \(\ln(2x+2) + c\)
- (C) \(\frac{1}{2}\ln(x^2+2x) + c\)
- (D) \(2\ln(x^2+2x) + c\)
Two types of material (A and B) are being tested for their ability to withstand different temperatures. A random selection of both materials was subjected to extreme temperature changes and then classified according to their condition after they were removed from the testing facility. The results are shown in the table.
| Material | |||
|---|---|---|---|
| A | B | Total | |
| Broke completely | 25 | 43 | 68 |
| Showed defects | 35 | 38 | 73 |
| Remained intact | 35 | 24 | 59 |
| Total | 95 | 105 | 200 |
An approximate 95% confidence interval for the probability that material A will break completely or show defects is given by
\[ \left( c - 1.96\sqrt{\frac{c(1-c)}{n}}, c + 1.96\sqrt{\frac{c(1-c)}{n}} \right) \]The values of \(c\) and \(n\) are
- (A) \(\frac{60}{95}\) and 95
- (B) \(\frac{60}{200}\) and 95
- (C) \(\frac{140}{200}\) and 95
- (D) \(\frac{60}{200}\) and 200
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Determine the derivative of each of the following with respect to \(x\).
a) \( y = \frac{1}{\sin(x)} \) [1 mark]
b) \( y = x^2 \times e^{-x} \)
Express your answer in factorised form. [2 marks]
An object is moving in a straight line from a fixed point. The object is at the origin initially.
The acceleration \(a\) (in m s\(^{-2}\)) of the object is given by
\[ a(t) = \pi \cos(\pi t) \quad t \ge 0, \text{where } t \text{ is time in seconds.} \]
The velocity at \(t = 1\) is 0.5 m s\(^{-1}\).
a) Determine the initial acceleration. [1 mark]
b) Determine the initial velocity. [2 marks]
c) Determine the displacement after one second. [2 marks]
A function is defined as \(f(x) = x(\ln(x))^2, x > 0\).
The graph of the function is shown and has a local maximum at point \(A\) and a global minimum at point \(B\).
The derivative of the function is given by \(f'(x) = 2 \ln(x) + (\ln(x))^2, x > 0\).
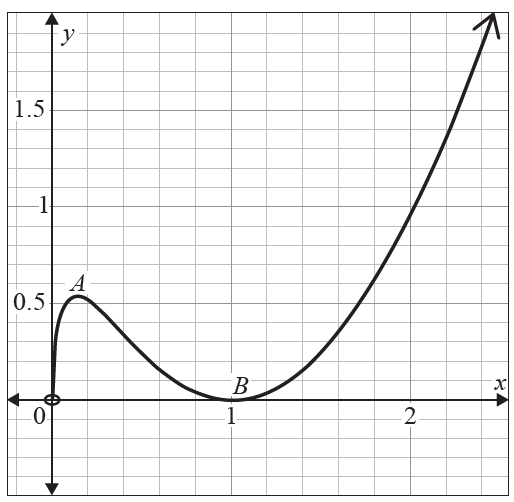
a) Verify that there is a stationary point at \(x = 1\). [2 marks]
b) Determine the coordinates of \(A\). [3 marks]
c) The graph of the function has a point of inflection at \(x = e^p\).
Determine \(p\). [2 marks]
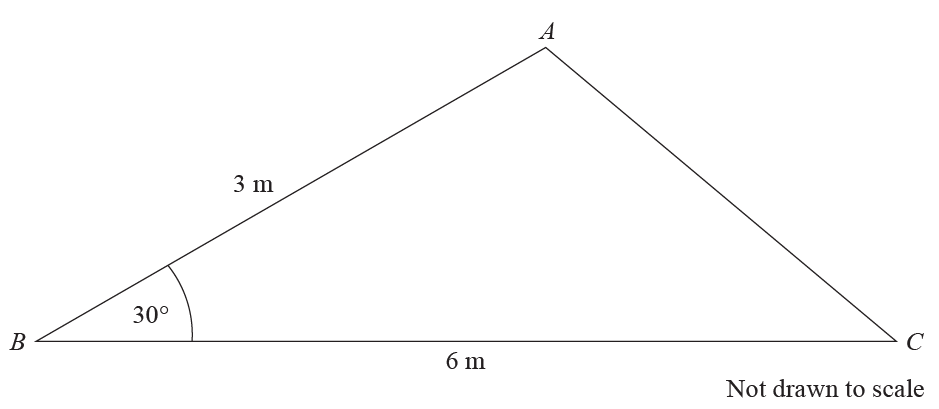
Determine the area of the triangle shown.
Solve the following equations.
a) \(4e^x = 100\) [1 mark]
b) \(2 \log_4 x - \log_4(x - 1) = 1\) [3 marks]
Consider the following graph of \(f(x)\).
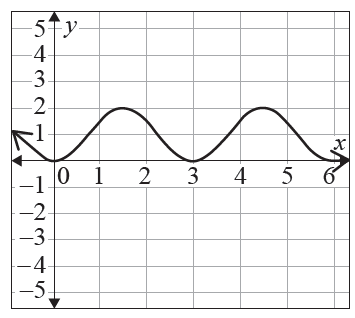
Identify the graph of the second derivative \(f''(x)\) from the graphs in Diagram 1, Diagram 2 and Diagram 3.
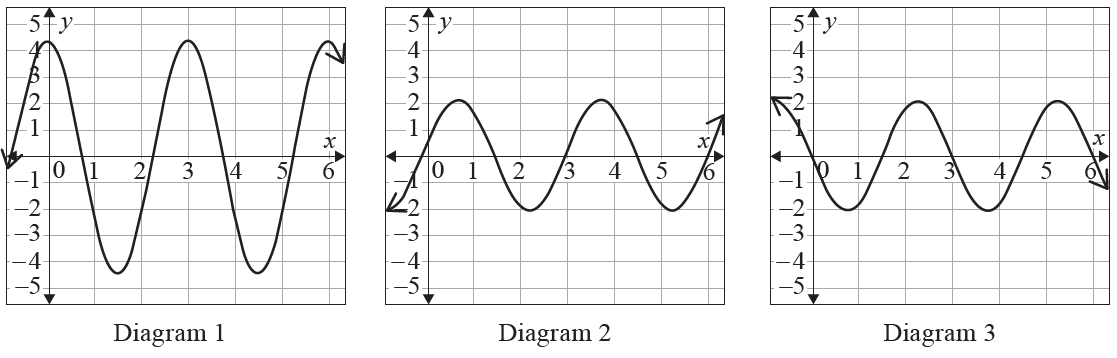
Justify your decisions using mathematical reasoning.
The volume of water in a tank is represented by a function of the form
\[ V(t) = Ae^{kt} \text{, where } V \text{ is in litres and } t \text{ is in minutes.} \]
Initially, the volume is 100 litres and it is decreasing by 50 litres per minute.
Determine the time at which the volume is decreasing at the rate of \( \frac{50}{7} \) litres per minute.
Express your answer in the form \(\ln(a)\).
The function \(f(x)\) has the form given by \(f(x) = 3 \log_2 (x + a) + b\)
The function \(g(x)\) has the form given by \(g(x) = -\log_3 (x + c) + 5\)
A section of the graphs of the two functions is shown.
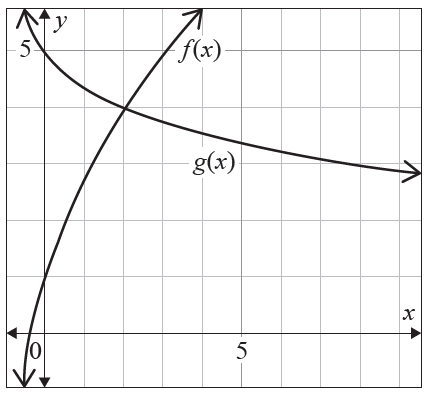
Determine the values of \(a\), \(b\) and \(c\).
A horizontal point of inflection is a point of inflection that is also a stationary point.
Determine the value/s of \(k\) for which the graph of \( f(x) = \frac{\ln(x)}{k} - \frac{kx}{x+1} \) has only one horizontal point of inflection.
At the end of the first stage of its growth cycle, a species of tree has a height of 5 metres and a trunk radius of 15 cm.
In the second stage of its growth cycle, the tree stays at this height for the next 10 years. However, the growth rate of the trunk radius (in cm per year) varies over the 10 years and is given by the function \[ r(t) = 1.5 + \sin\left(\frac{\pi t}{5}\right) \] Assume the density (mass per unit volume) of the tree trunk is approximately 1 g/cm\(^3\) and the tree trunk is in the shape of a cylinder.
Determine the ratio of the trunk's mass at the end of the second stage to its mass at the end of the first stage.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/