QCAA Maths Methods 2021 Exam 2 with solutions
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
The scores obtained on a test can be assumed to be normally distributed with a mean of 102 and a standard deviation of 19.
What proportion of scores are over 113?
- (A) 0.2813
- (B) 0.5789
- (C) 0.7187
- (D) 0.8216
A substance is being heated such that its temperature \(T\) in °C after \(t\) minutes is given by the function \(T = 2e^{0.5t}\).
The first integer value of \(t\) for which the instantaneous rate of change of temperature is greater than 100 °C per minute is
- (A) \(t=10\)
- (B) \(t=9\)
- (C) \(t=8\)
- (D) \(t=7\)
A random sample of people were surveyed about the most important factor when deciding where to shop. The results appear in the table.
| Factor | Percentage (%) |
|---|---|
| Price | 40 |
| Quality of merchandise | 30 |
| Service | 15 |
| Shopping environment | 15 |
If the sample size was 1200, the approximate 95% confidence interval for the proportion of people who identified price as the most important factor is
- (A) (0.395, 0.405)
- (B) (0.386, 0.414)
- (C) (0.377, 0.423)
- (D) (0.372, 0.428)
Using the trapezoidal rule with an interval size of 1, the approximate value of the integral \(\int_0^3 0.5^x dx\) is
- (A) 1.25
- (B) 1.26
- (C) 1.31
- (D) 1.88
Solve for \(x\) given that \(\log_3(x-1) = 2\).
- (A) 7
- (B) 8
- (C) 9
- (D) 10
When seeds of a certain variety of flower are planted, the probability of each seed germinating is 0.8.
If eight seeds are planted, what is the probability that at least six seeds will germinate?
- (A) 0.797
- (B) 0.503
- (C) 0.294
- (D) 0.001
Determine \(f(x)\), given \(f'(x) = 6x^2 + \frac{1}{x^2} + \frac{1}{x}\) and \(f(1) = 5\).
- (A) \(f(x) = 2x^3 + \frac{3}{x^3} + \ln(x) - 1\)
- (B) \(f(x) = 2x^3 - \frac{1}{x} + \ln(x) + 4\)
- (C) \(f(x) = 2x^3 - \frac{1}{x} + \frac{2}{x^2} + 2\)
- (D) \(f(x) = 2x^3 + \frac{3}{x^3} + \frac{2}{x^2} - 2\)
The displacement (in metres) of a particle is given by \(s(t) = -3\cos(t) + 2\sin(t)\), where \(t\) is in seconds.
The instantaneous velocity of the particle at time \(t = \frac{\pi}{2}\) seconds is
- (A) -3 m s\(^{-1}\)
- (B) -2 m s\(^{-1}\)
- (C) 2 m s\(^{-1}\)
- (D) 3 m s\(^{-1}\)
The graphs of the functions \(f(x) = 2e^x + 5\) and \(g(x) = \frac{3}{e^x}\) intersect at point A. Determine the coordinates of point A.
- (A) (1.609, 15)
- (B) (1.099, 1)
- (C) (0.4065, 2)
- (D) (-0.693, 6)
An object travels in a straight line so that its velocity at time \(t\) seconds is given by \(v(t) = 2t + \sin(2t)\). Determine the expression for acceleration as a function of time.
- (A) \(a(t) = 2 + 2\cos(2t)\)
- (B) \(a(t) = 2 - \frac{1}{2}\cos(2t)\)
- (C) \(a(t) = t^2 + 2\cos(2t)\)
- (D) \(a(t) = t^2 - \frac{1}{2}\cos(2t)\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
Consider the function \( f(x) = e^x \sin(x) \), \( 0 \le x \le 2\pi \)
a) State the exact values of the x-intercepts of the graph of \( f(x) \). [2 marks]
b) Write an expression for the area enclosed between the graph of \( f(x) \) and the x-axis. [2 marks]
c) Determine the area enclosed between the graph of \( f(x) \) and the x-axis to the nearest square unit. [1 mark]
The velocity function of an object in m s\(^{-1}\) is given by \( v(t) = \cos\left(6t+\frac{\pi}{2}\right) + 2 \), \( 0 \le t \le 5 \). Initially, the object is at the origin.
a) Determine the displacement function. [2 marks]
b) What is the displacement of the object from the origin, in metres (m), after three seconds? [2 marks]
The amount of gravel (in tonnes) sold by a construction company in a given week is a continuous random variable \(X\) and has a probability density function defined by: \[ f(x) = \begin{cases} c(1-x^2), & 0 \le x \le 1 \\ 0, & \text{otherwise} \end{cases} \]
a) Show that \( c = \frac{3}{2} \). [1 mark]
b) Determine \( P(X < 0.25) \). [2 marks]
c) Determine the variance of \(X\). [4 marks]
The heights of students at School A are normally distributed with a mean of 165 cm and a standard deviation of 15 cm.
a) Determine the probability that a student chosen at random from School A is shorter than 180 cm. [1 mark]
b) Determine the minimum integer value of the height of a student who is in the top 2% of this distribution. [3 marks]
The heights of students at School B are also normally distributed. A student at School B has the same height as the height determined in Question 14b) but their corresponding z-score is 3.
c) Determine which student's height ranks higher in terms of percentile for their school. [3 marks]
A new internet search engine gives a ranking \(R\) to each website based on the function \( R = \log_{10}(50h^2) \), where \(h\) is the number of hits (visits) the website has received.
If a website currently has 100 hits, determine how many more hits they need to increase their ranking by 1.
In the diagram DC represents a 60 metre vertical tower.
A and B are two points in the same horizontal plane as the foot C of the tower.
The angle above the horizontal from A to D is 28° and the angle above the horizontal from B to D is 35°.
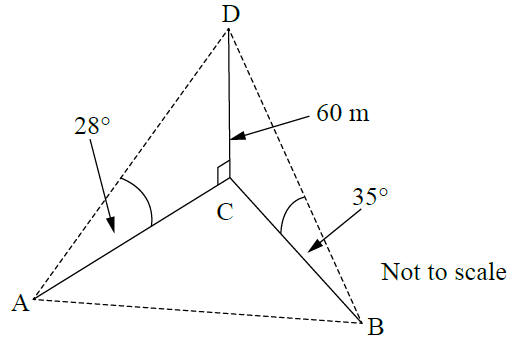
The bearing of C from A is 050°T and the bearing of C from B is 300°T.
Determine the distance between A and B to the nearest metre.
Rabbits and foxes are among two species of mammals that live on an isolated island.
Rabbits represent a significant food source for the foxes.
The populations of rabbits and foxes were monitored each month for two years.
The graph shows the population of foxes (in thousands) and the population of rabbits (in thousands), at any time \(t\) (in months) over the two years. The two populations can be modelled using trigonometric functions.
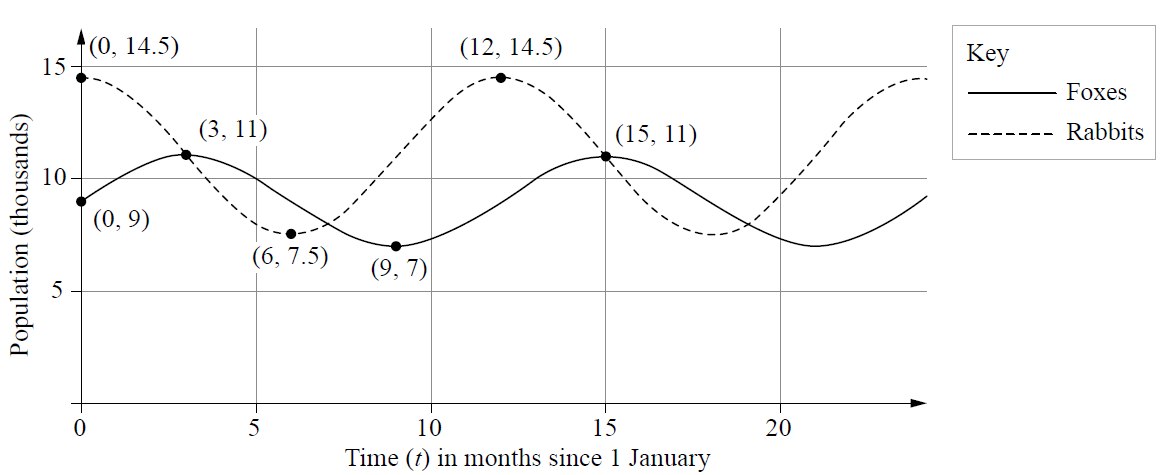
Jane believes that there were periods of time over the two years when the total population of foxes and rabbits on the island exceeded 25 000.
Evaluate the reasonableness of Jane's claim.
The number of animals in a population (in thousands) is modelled by the function \(P\) such that \[ P(t) = \frac{100}{1+4e^{-t}} \] where \(t\) is in years.
Determine the number of animals in the population when the population is growing the fastest.
A random variable \(X\), defined over the interval \(a \le x \le b\), is uniformly distributed if its probability density function is defined by: \[ f(x) = \begin{cases} \frac{1}{b-a}, & a \le x \le b \\ 0, & \text{otherwise} \end{cases} \]
The expected value and variance of a uniform random variable \(X\) are \[ E(X) = \frac{(a+b)}{2} \quad \text{Var}(X) = \frac{(b-a)^2}{12} \]
A manufacturer has observed that the time that elapses between placing an order with a supplier and the delivery of the order is uniformly distributed between 100 and 180 minutes.
Determine the probability that the time between placing an order and delivery of the order will be within one standard deviation of the expected time.
The random variable \(B\) is normally distributed with a mean of 0 and a standard deviation of 1.
Determine the probability that the quadratic equation \( x^2 + 3x + 2B = 0 \) has real roots.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/