2024 QCAA Maths Methods External Exam Paper 2
Paper 2 — Technology-active
This is the full QCE Maths Methods External Exam with worked solutions. You can also try Mini-Tests, which are official QCAA exams split into short tests you can do anytime.
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
The probability of hitting a target in a particular binomial experiment is \(0.72\). Determine the mean of the number of hits if this experiment is repeated eight times.
- (A) 1.61
- (B) 2.24
- (C) 5.76
- (D) 7.28
Calculate the expected value of a continuous random variable \(X\) with the probability density function
- (A) 1.72
- (B) 1.15
- (C) 1.00
- (D) 0.11
The derivative of the function \(f(x)\) is given by \(f'(x) = \sin(2x)\). It is known that \(f\left(\frac{\pi}{2}\right) = 4\). Determine \(f(x)\).
- (A) \(-\cos(2x) + 3\)
- (B) \(\cos(2x) + 5\)
- (C) \(-\frac{1}{2}\cos(2x) + 3.5\)
- (D) \(\frac{1}{2}\cos(2x) + 4.5\)
Consider the Bernoulli distribution where the outcomes for rolling a six-sided die are a four and not rolling a four. Determine the variance of the resulting Bernoulli distribution in this scenario.
- (A) 0.027˙
- (B) 0.138˙
- (C) 0.16
- (D) 0.83
The mass (g) of adult kookaburras in a certain region is normally distributed with a mean of 300 g and a standard deviation of 13 g. Select the correct statement about the mass of adult kookaburras.
- (A) 34% are between 287 g and 313 g
- (B) 68% are between 274 g and 326 g
- (C) 95% are between 261 g and 326 g
- (D) 99.7% are between 261 g and 339 g
Determine the derivative of \(y = 2x \cos(3x)\).
- (A) \(2\cos(3x) - 6x \sin(3x)\)
- (B) \(2\cos(3x) + 6x \sin(3x)\)
- (C) \(-6\sin(3x)\)
- (D) \(-2\sin(3x)\)
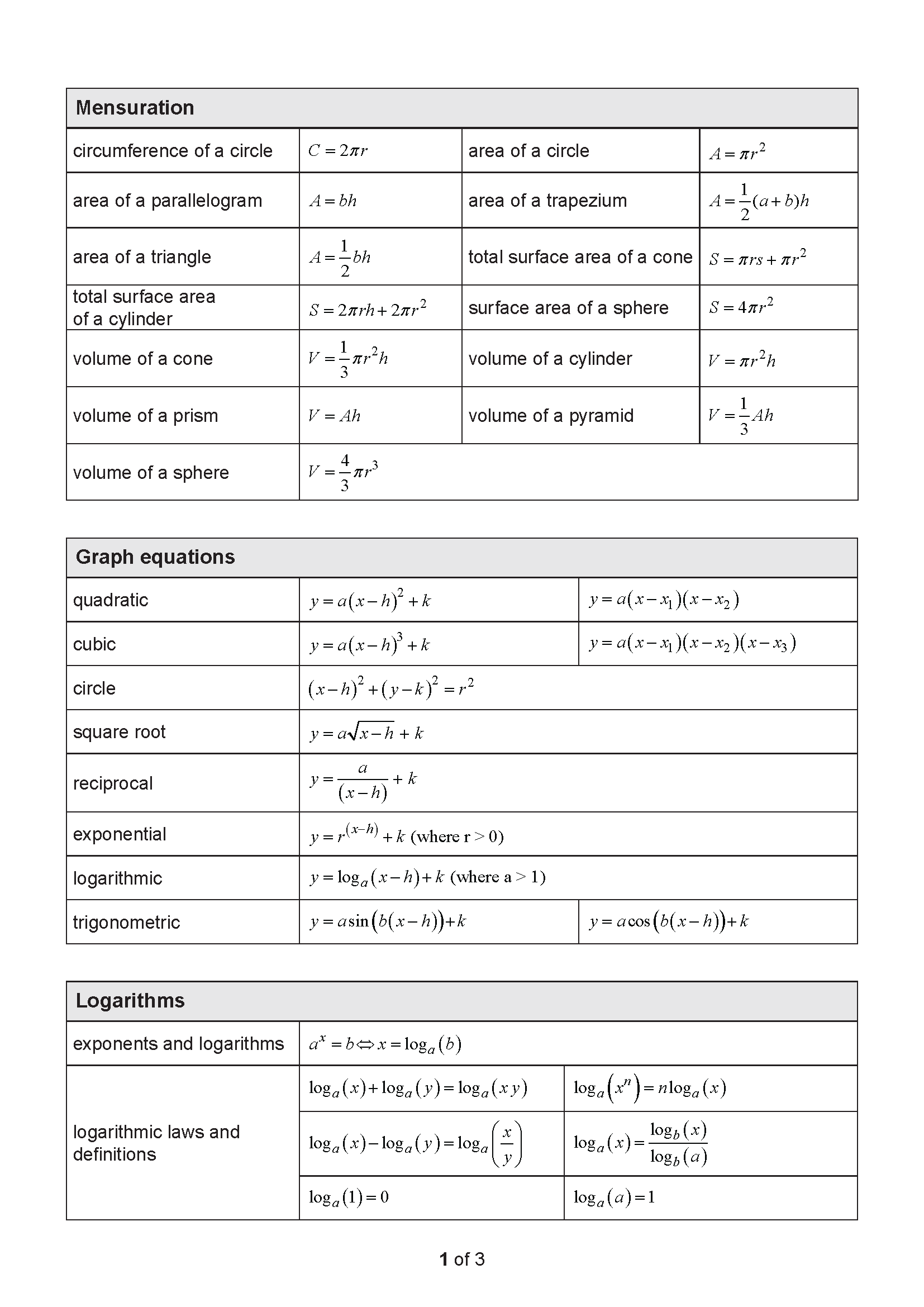
Identify the possible values for \(a\) in the triangle.
- (A) \(13.5^\circ\) or \(126.5^\circ\)
- (B) \(53.5^\circ\) or \(126.5^\circ\)
- (C) \(53.5^\circ\) or \(86.5^\circ\)
- (D) \(13.5^\circ\) or \(86.5^\circ\)
Calculate the total enclosed area between the graph of \(y=x^2-x-6\) and the \(x\)-axis from \(x=1\) to \(x=5\).
- (A) 5.33
- (B) 7.33
- (C) 12.67
- (D) 20.00
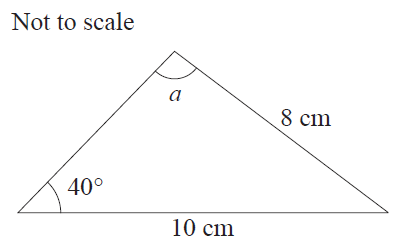
It is known that \(f'(x) = 0\) and \(f''(x) < 0\) for one of the labelled points on the graph of \(f(x)\).
Which point matches this description?
- (A) \(P\)
- (B) \(Q\)
- (C) \(R\)
- (D) \(S\)
The velocity (m s\(^{-1}\)) at time \(t\) (s) of an object is given by \(v(t) = 0.4t^2 + 3t\) for \(t \ge 0\). The change in displacement (m) of the object from four to five seconds is
- (A) 15.43
- (B) 21.63
- (C) 32.53
- (D) 54.17
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
State the trapezoidal rule and use it with six strips to determine an approximate value of the definite integral for the curve of \(f(x) = 4(x-3)^2\) from \(x = 0\) to \(x = 3\). Show all substitutions made into the rule.
The magnitude of an earthquake can be modelled by the logarithmic equation \(M_A = \log_{10} \left( \frac{I_A}{I_0} \right)\), where \(M_A\) is the magnitude at a location A, \(I_A\) is the intensity of the earthquake at location A and \(I_0\) is a constant.
An earthquake at location P had a magnitude of 5.2.
A different earthquake at location Q had a magnitude of 3.5.
a) Determine an equation involving logarithms that expresses the difference in magnitudes between the earthquakes at locations P and Q. [1 mark]
b) How many times more intense was the earthquake at location P than the earthquake at location Q? [4 marks]
The number of termites in a particular nest can be modelled by \(N(t) = \frac{A}{2+e^{-t}}\), where \(A\) is a constant and \(t\) represents time (months) since the nest first became a visible mound above ground level.
It is estimated that when the mound first became visible, the population was \(3 \times 10^5\) termites.
a) Determine the value of \(A\). [1 mark]
b) Determine the number of termites in the nest half a year after the mound became visible. [2 marks]
c) Determine the time in months after the mound became visible for the initial population to increase by 130 000 termites. Express the time as a decimal. [2 marks]
d) Develop a formula for the rate of change in the number of termites at any time after the mound became visible. Express your formula as a fraction. [2 marks]
e) Determine the rate of change in the number of termites five months after the mound became visible. [1 mark]
A football coach offered a 12-day intensive training clinic. During the clinic, the height that each player could kick a football was monitored.
One player's kick heights could be modelled by \(H(t) = \log_{10}(10t+10)+5\), \(0 \le t \le 12\), where \(H(t)\) is vertical height (m) and \(t\) is the time (days) spent in training.
a) Determine the initial height that the player could kick the ball. [1 mark]
b) Determine the training time needed for the player to be able to kick the ball to a height of 7 m. [1 mark]
c) Determine the overall improvement in kick height achieved by completing the clinic. [2 marks]
d) Determine the rate of change in kick height when \(t = 1.5\) days. [1 mark]
e) Determine the training time (as a decimal) when the rate of change in kick height is 0.09 m/day. [1 mark]
The term extremely tall is used to describe any person whose height is three standard deviations or more above the mean height of the population.
A person who just qualifies as extremely tall in a country where heights are normally distributed with a mean height of 180 cm and a standard deviation of 10 cm travels to another country. The person discovers they are taller than exactly 90% of the destination country's population.
Assuming that the standard deviation of both countries is the same, determine the minimum height required to be considered extremely tall in the destination country.
At council meetings in a particular town, new proposals are only discussed if more than 80% of the community are in favour of the proposal.
To discover community opinion on a new bus route proposal, the council conducted several surveys, each with a sample size of 120. The distribution of the sample proportions from the surveys had a standard deviation of 0.04.
Make a justified decision as to whether the new bus route proposal would be discussed at a council meeting.
At a particular orchard, 3% of fruit is bruised during picking. After picking, the fruit is packed into boxes, each containing four pieces of fruit.
A grocery shop orders 140 boxes of fruit to sell to their customers.
Determine the expected number of boxes that will contain bruised fruit.
An object experiencing straight-line motion along a path has an acceleration (m s\(^{-2}\)) defined by the function \(a(t) = 3\sin(2t)\) where \(t\) is time (s) since the object begins moving, \(t \ge 0\).
When \(t=0\), both displacement and velocity are zero.
On the path is a motion sensor that is able to detect motion up to 2 metres away.
The object passes directly by the motion sensor when \(t=3\).
Determine the average velocity of the object while it moves through the range of the sensor.
The normal distribution probability density function is \[ p(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^2} \] with the parameters mean, \(\mu\), and standard deviation, \(\sigma\).
The speeds of electric scooter (e-scooter) riders on a particular section of a bike path are approximately normally distributed with a mean of 18 km/h. It is known that \(p(10) = 0.0135\).
The speed limit for e-scooters on this section of bike path is 23 km/h.
A speed camera is set up and records the speeds of 75 e-scooter riders. Every rider travelling faster than the speed limit is given a $143 fine. Before setting up the speed camera, the following suggestion was made.
Evaluate the reasonableness of this suggestion.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/