2024 QCAA Maths Methods External Exam Paper 1
Paper 1 — Technology-free
This is the full QCE Maths Methods External Exam with worked solutions. You can also try Mini-Tests, which are official QCAA exams split into short tests you can do anytime.
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
Determine \(\int x^4 dx\)
- (A) \(4x^3 + c\)
- (B) \(5x^5 + c\)
- (C) \(\frac{1}{3}x^3 + c\)
- (D) \(\frac{1}{5}x^5 + c\)
Determine \(\frac{dy}{dx}\) for the function \(y = e^{\sin(x)}\)
- (A) \(\cos(x) e^{\sin(x)}\)
- (B) \(\sin(x) e^{\cos(x)}\)
- (C) \(e^{\sin(x)}\)
- (D) \(e^{\cos(x)}\)
A sample of size \(n\) can be used to obtain a sample proportion \(\hat{p}\). An approximate margin of error for the population proportion can be obtained using the formula
\[E = z\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]If the level of confidence is increased from 95% to 99%, then
- (A) the associated \(z\)-value would decrease, so \(E\) would increase.
- (B) the associated \(z\)-value would increase, so \(E\) would increase.
- (C) the associated \(z\)-value would decrease, so \(E\) would decrease.
- (D) the associated \(z\)-value would increase, so \(E\) would decrease.
Simplify \(y = 2\ln(e^x)\)
- (A) \(y = 2x\)
- (B) \(y = 2^x\)
- (C) \(y = \frac{2}{x}\)
- (D) \(y = x^2\)
Determine \(\int_a^b 2\cos(x)dx\), where \(a = \frac{\pi}{3}\) and \(b = \frac{\pi}{2}\).
- (A) \(1 - \frac{\sqrt{3}}{2}\)
- (B) \(\frac{\sqrt{3}}{2} - 1\)
- (C) \(2 - \sqrt{3}\)
- (D) \(\sqrt{3} - 2\)
Differentiate \(y = \ln(x)\cos(x)\) with respect to \(x\).
- (A) \(\frac{\cos(x)}{x}\)
- (B) \(-\frac{\sin(x)}{x}\)
- (C) \(\frac{\cos(x)}{x} + \ln(x)\sin(x)\)
- (D) \(\frac{\cos(x)}{x} - \ln(x)\sin(x)\)
Twenty families are selected to participate in a lifestyle study related to family size. The number of children in these families is uniformly distributed as shown.
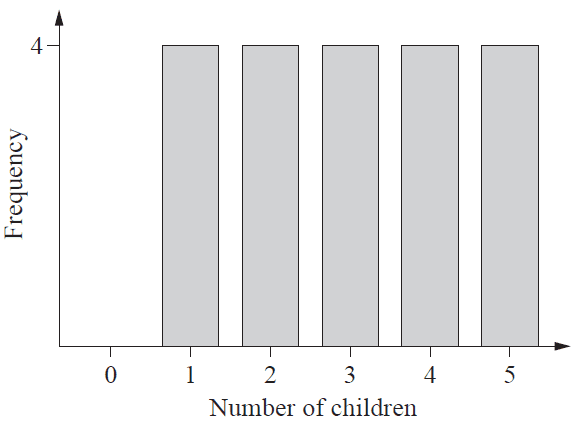
A random sample of five families is chosen from this group, without replacement. A possible mean number of children in the sample is
- (A) 5.0
- (B) 2.0
- (C) 1.0
- (D) 0.0
The graph of \(f(x)\) is shown.
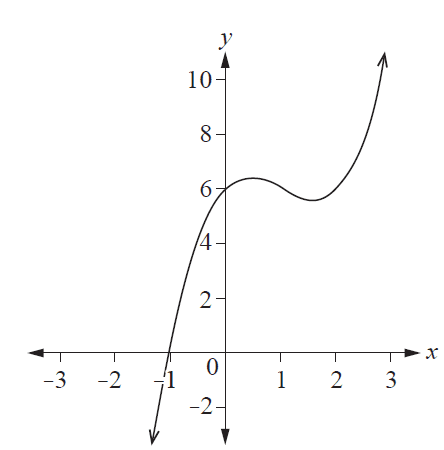
Identify the graph of the second derivative \(f''(x)\).
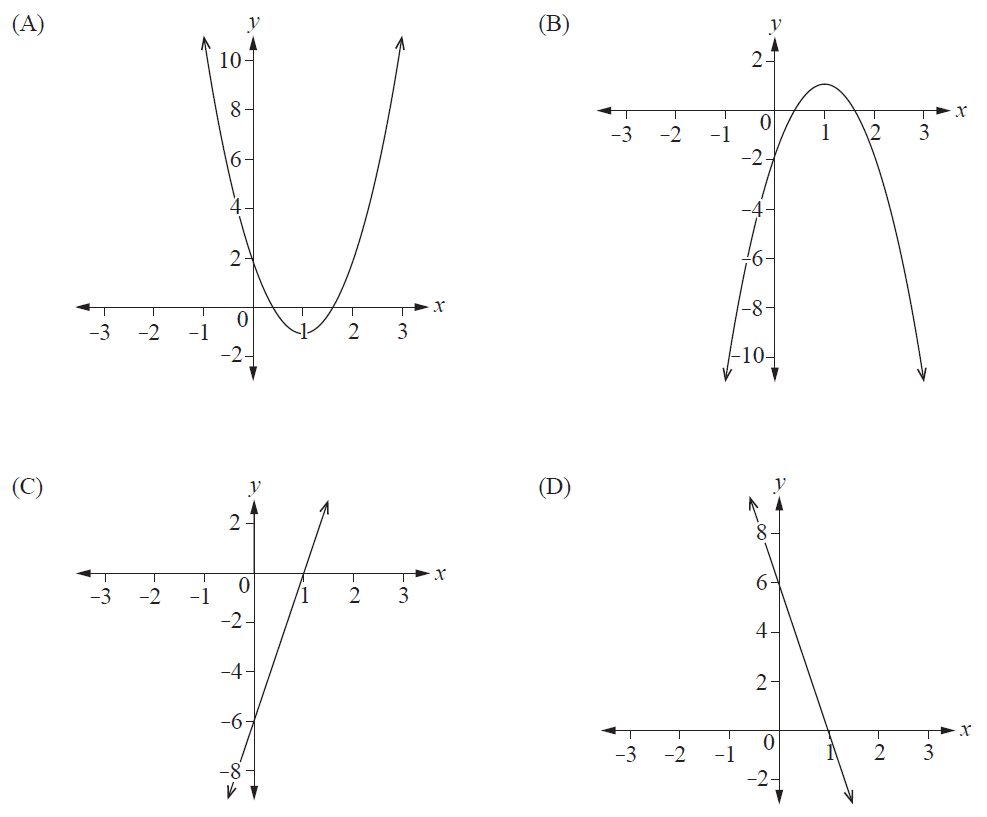
At a certain location, the temperature (°C) can be modelled by the function \(T = 5\sin\left(\frac{\pi}{12}x\right) + 23\), where \(x\) is the number of hours after sunrise.
Determine the rate of change of temperature (°C/hour) when \(x = 4\).
- (A) \(\frac{5\pi}{48}\)
- (B) \(\frac{5\pi}{24}\)
- (C) \(\frac{5\pi\sqrt{3}}{24}\)
- (D) \(\frac{5\pi\sqrt{3}}{6}\)
Given that \(\log_{10} 6 = 0.778\), determine the value of \(\log_{10} 600\).
- (A) 77.800
- (B) 10.778
- (C) 2.778
- (D) 1.556
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
a) Determine the second derivative of \(y = x^3 - 3x^2\). [2 marks]
b) Use your result from Question 11a) to calculate the value of the second derivative when \(x = -1\). [1 mark]
c) Determine the x- and y-coordinates of the point on the graph of \(y = x^3 - 3x^2\) for which the rate of change of the first derivative is zero. [3 marks]
Each day over a three-day long weekend, a family spins a pointer on a circular board to decide whether they will spend the day at the beach or bushwalking. The circular board consists of three equal sections.
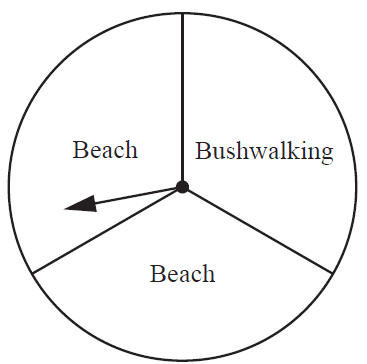
a) Determine the probability that the family will spend all three days bushwalking. [1 mark]
b) Determine the following binomial probabilities, expressed as fully simplified fractions.
i. Exactly two days will be spent at the beach. [2 marks]
ii. Fewer than three days will be spent at the beach. [3 marks]
a) \(F(x) = \int (4e^{2x} + \sin(2x)) \, dx\). Use integration to determine \(F(x)\), if \(F(0) = 5\). [3 marks]
b) If \(\frac{dy}{dx} = \left( \frac{3x^7 - 2x}{x^4} \right)^2\), determine \(y\). [3 marks]
At a particular game at a local sporting venue, 60% of spectators support the home team and the remainder support the away team.
A researcher asked six groups of 10 spectators which team they supported. Each spectator was recorded as either H (supports home team) or A (supports away team). The results were:
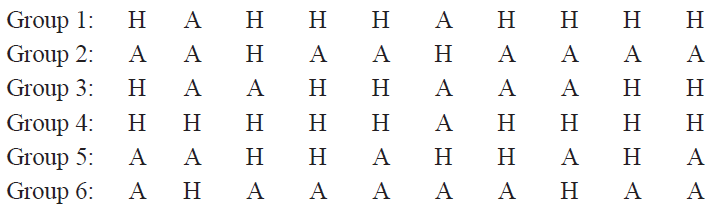
a) The researcher would like to see the distribution of the sample proportions of home team supporters obtained by entering the information into a column graph. The sample proportion for group 1 is shown.
Complete the column graph by including the sample proportions for the remaining five groups. [3 marks]

Note: If you make a mistake in the diagram, cancel it by ruling a single diagonal line through your work and use the additional response space at the back of this question and response book.
b) If the researcher had interviewed more groups, each containing 100 spectators, describe two ways the distribution of the resulting sample proportions would be expected to differ from the distribution shown in Question 14a). [2 marks]
A survey was conducted to understand whether people support a new policy.
Using a \(z\)-score of 2, the approximate confidence interval for the population proportion of people who support the policy was calculated as
\[ \left( \frac{3}{10}, \frac{7}{10} \right) \]a) Determine the margin of error. [1 mark]
b) Determine the number of people surveyed. [3 marks]
The graph is of the form \(y = \log_a (x + b)\). A point on the graph \((4, 3)\) is labelled. The line \(x = -4\) is an asymptote.
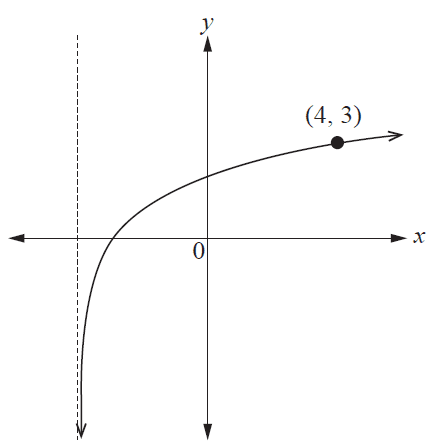
There is a point \(P(x_p, y_p)\) on the graph where \(y_p\) is twice the value of the \(y\)-intercept of the curve. Determine the value of \(x_p\).
A community group that uses social media created a new post on the internet on a day when they had 1000 members. The rate of change in their number of members (members/day) is given by \(f'(t) = 3e^{0.5t}\), where \(t\) represents days after the new post.
Determine the time it will take for the community group to achieve seven times the initial number of members. Express your answer in the form \(a\ln(b)\).
The diagram shows some dimensions of a large storage container that is a rectangular prism. The angle \(\angle ABC\) is \(60^\circ\).
A person requires a container that is at least 4 metres in height.
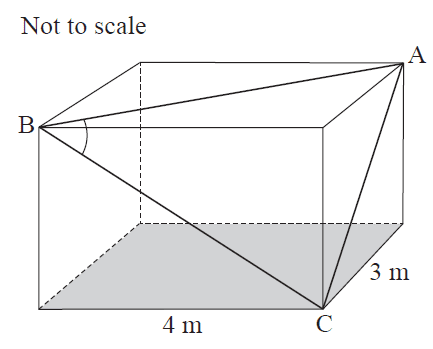
Make a justified decision about whether this storage container meets the person’s requirements.
A permanent ice glacier is in a valley in New Zealand.
Due to the temperature changes of the seasons each year, the glacier expands for six months and recedes for six months. The changing distance of a point on the front edge of the glacier to a car park can be modelled by a sine function.
During the colder months, when the glacier expands, the front edge of the glacier moves to within 270 m of the car park. However, in the warmer months, when the glacier recedes, the front edge moves to a maximum distance of 280 m away from the car park.
The erosion effects of the glacier on the ground are of most interest to geologists when the absolute value of the acceleration of the front edge is greater than \(\frac{5\pi^2\sqrt{3}}{72}\) metres/month\(^2\). During these times, a team of geologists sets up a camp site nearby to perform field work. Whenever the acceleration is less than this, the geologists leave camp.
The following claim is made.
The geologists will spend a total of between seven and eight months at the camp site each calendar year.
Evaluate the reasonableness of this claim.
END OF PAPER
2024 QCAA Maths Methods External Exam Paper 1
Paper 1 — Technology-free
This is the full QCE Maths Methods External Exam with worked solutions. You can also try Mini-Tests, which are official QCAA exams split into short tests you can do anytime.
Number of marks: 55
Perusal time: 5 minutes
Writing time: 90 minutes
Section 1
Instructions
• This section has 10 questions and is worth 10 marks.
• Use a 2B pencil to fill in the A, B, C or D answer bubble completely.
• Choose the best answer for Questions 1 10.
• If you change your mind or make a mistake, use an eraser to remove your response and fill in the new answer bubble completely.
\(e^{\ln(x)}\) is equivalent to
- (A) \(0\)
- (B) \(1\)
- (C) \(x\)
- (D) \(\frac{1}{x}\)
If \(f(x) = e^{6-2x}\), determine the value of \(f'(2)\).
- (A) \(e^2\)
- (B) \(2e^2\)
- (C) \(-e^2\)
- (D) \(-2e^2\)
A bag contains 10 buttons of the same shape and size in different colours: 5 blue, 3 green and 2 red. If 3 buttons are randomly drawn from the bag, which probability can be calculated using the binomial distribution?
- (A) \(P(3 \text{ green})\) with replacement
- (B) \(P(3 \text{ blue})\) without replacement
- (C) \(P(2 \text{ green and } 1 \text{ red})\) with replacement
- (D) \(P(2 \text{ red and } 1 \text{ blue})\) without replacement
If the gradient of the function \(f(x)\) is given by \(\frac{20}{x^3}\), then \(f(x)\) is equal to
- (A) \(-\frac{60}{x^4} + c\)
- (B) \(-\frac{5}{x^4} + c\)
- (C) \(-\frac{10}{x^2} + c\)
- (D) \(-\frac{40}{x^2} + c\)
Determine \(\int_1^3 \frac{1}{2x} dx\).
- (A) \(\frac{1}{2} \ln 6\)
- (B) \(\frac{1}{2} \ln 5\)
- (C) \(\frac{1}{2} \ln 4\)
- (D) \(\frac{1}{2} \ln 3\)
Substitutions for \(h\) are used to estimate the limit of \(\frac{a^h - 1}{h}\) as \(h \to 0\). Which sequence is the most appropriate?
- (A) \(-4, -2, -1, -0.5, -0.25, -0.125 \dots\)
- (B) \(-0.05, -0.1, -0.2, -0.4, -0.8 \dots\)
- (C) \(2, 1, 0, -1, -2, -3 \dots\)
- (D) \(1, 2, 3, 4, 5, 6 \dots\)
Determine the mean of the continuous random variable \(X\) with the probability density function
\[ f(x) = \begin{cases} \frac{1}{8}x, & 0 \le x \le 4 \\ 0, & \text{otherwise} \end{cases} \]- (A) \(\frac{1}{8}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{1}{2}\)
- (D) \(\frac{8}{3}\)
A sample of size \(n\) was used to estimate a population proportion. An approximate margin of error of 3% was calculated using \(z = 1.96\). Given the sample proportion was 0.6, determine \(n\).
- (A) \(n = \frac{\left(\frac{0.03}{1.96}\right)^2}{0.24}\)
- (B) \(n = \frac{0.24}{\left(\frac{0.03}{1.96}\right)^2}\)
- (C) \(n = \frac{\left(\frac{0.03}{1.96}\right)^2}{2.4}\)
- (D) \(n = \frac{2.4}{\left(\frac{0.03}{1.96}\right)^2}\)
Determine \(\int_0^3 \pi \sin\left(\frac{\pi}{3}x\right)dx\).
- (A) \(3\)
- (B) \(6\)
- (C) \(-3\)
- (D) \(-6\)
The continuous random variable \(Y\) has the probability density function
\[ f(y) = \begin{cases} 1+y, & 0 \le y \le \sqrt{3}-1 \\ 0, & \text{otherwise} \end{cases} \]Determine \(P(0 \le y \le \frac{1}{2})\).
- (A) \(\frac{1}{5}\)
- (B) \(\frac{3}{8}\)
- (C) \(\frac{5}{8}\)
- (D) \(\frac{3}{4}\)
Section 2
Instructions
• Write using black or blue pen.
• Questions worth more than one mark require mathematical reasoning and/or working to be shown to support answers.
• If you need more space for a response, use the additional pages at the back of this book.
– On the additional pages, write the question number you are responding to.
– Cancel any incorrect response by ruling a single diagonal line through your work.
– Write the page number of your alternative/additional response, i.e. See page …
– If you do not do this, your original response will be marked.
• This section has nine questions and is worth 45 marks.
a) Determine the second derivative of \(y = x^3 - 3x^2\). [2 marks]
b) Use your result from Question 11a) to calculate the value of the second derivative when \(x = -1\). [1 mark]
c) Determine the x- and y-coordinates of the point on the graph of \(y = x^3 - 3x^2\) for which the rate of change of the first derivative is zero. [3 marks]
Each day over a three-day long weekend, a family spins a pointer on a circular board to decide whether they will spend the day at the beach or bushwalking. The circular board consists of three equal sections.

a) Determine the probability that the family will spend all three days bushwalking. [1 mark]
b) Determine the following binomial probabilities, expressed as fully simplified fractions.
i. Exactly two days will be spent at the beach. [2 marks]
ii. Fewer than three days will be spent at the beach. [3 marks]
a) \(F(x) = \int (4e^{2x} + \sin(2x)) \, dx\). Use integration to determine \(F(x)\), if \(F(0) = 5\). [3 marks]
b) If \(\frac{dy}{dx} = \left( \frac{3x^7 - 2x}{x^4} \right)^2\), determine \(y\). [3 marks]
At a particular game at a local sporting venue, 60% of spectators support the home team and the remainder support the away team.
A researcher asked six groups of 10 spectators which team they supported. Each spectator was recorded as either H (supports home team) or A (supports away team). The results were:
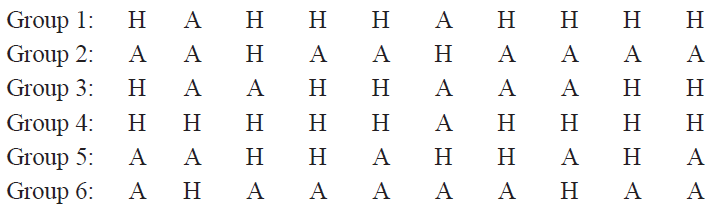
a) The researcher would like to see the distribution of the sample proportions of home team supporters obtained by entering the information into a column graph. The sample proportion for group 1 is shown.
Complete the column graph by including the sample proportions for the remaining five groups. [3 marks]

Note: If you make a mistake in the diagram, cancel it by ruling a single diagonal line through your work and use the additional response space at the back of this question and response book.
b) If the researcher had interviewed more groups, each containing 100 spectators, describe two ways the distribution of the resulting sample proportions would be expected to differ from the distribution shown in Question 14a). [2 marks]
A survey was conducted to understand whether people support a new policy.
Using a \(z\)-score of 2, the approximate confidence interval for the population proportion of people who support the policy was calculated as
\[ \left( \frac{3}{10}, \frac{7}{10} \right) \]a) Determine the margin of error. [1 mark]
b) Determine the number of people surveyed. [3 marks]
The graph is of the form \(y = \log_a (x + b)\). A point on the graph \((4, 3)\) is labelled. The line \(x = -4\) is an asymptote.

There is a point \(P(x_p, y_p)\) on the graph where \(y_p\) is twice the value of the \(y\)-intercept of the curve. Determine the value of \(x_p\).
A community group that uses social media created a new post on the internet on a day when they had 1000 members. The rate of change in their number of members (members/day) is given by \(f'(t) = 3e^{0.5t}\), where \(t\) represents days after the new post.
Determine the time it will take for the community group to achieve seven times the initial number of members. Express your answer in the form \(a\ln(b)\).
The diagram shows some dimensions of a large storage container that is a rectangular prism. The angle \(\angle ABC\) is \(60^\circ\).
A person requires a container that is at least 4 metres in height.

Make a justified decision about whether this storage container meets the person’s requirements.
A permanent ice glacier is in a valley in New Zealand.
Due to the temperature changes of the seasons each year, the glacier expands for six months and recedes for six months. The changing distance of a point on the front edge of the glacier to a car park can be modelled by a sine function.
During the colder months, when the glacier expands, the front edge of the glacier moves to within 270 m of the car park. However, in the warmer months, when the glacier recedes, the front edge moves to a maximum distance of 280 m away from the car park.
The erosion effects of the glacier on the ground are of most interest to geologists when the absolute value of the acceleration of the front edge is greater than \(\frac{5\pi^2\sqrt{3}}{72}\) metres/month\(^2\). During these times, a team of geologists sets up a camp site nearby to perform field work. Whenever the acceleration is less than this, the geologists leave camp.
The following claim is made.
The geologists will spend a total of between seven and eight months at the camp site each calendar year.
Evaluate the reasonableness of this claim.
END OF PAPER
QCE is a registered trademark of the QCAA. The QCAA does not endorse or make any warranties regarding this study resource. Past QCE exams and related content can be accessed directly at www.qcaa.qld.edu.au/