2016 VCE Maths Methods Mini Test 9
Number of marks: 10
Reading time: 2 minutes
Writing time: 15 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The function \(f\) has the property \(f(x) - f(y) = (y-x)f(xy)\) for all non-zero real numbers \(x\) and \(y\).
Which one of the following is a possible rule for the function?
- A. \(f(x) = x^2\)
- B. \(f(x) = x^2 + x^4\)
- C. \(f(x) = x\log_e(x)\)
- D. \(f(x) = \frac{1}{x}\)
- E. \(f(x) = \frac{1}{x^2}\)
The graph of a function \(f\) is obtained from the graph of the function \(g\) with rule \(g(x) = \sqrt{2x-5}\) by a reflection in the \(x\)-axis followed by a dilation from the \(y\)-axis by a factor of \(\frac{1}{2}\).
Which one of the following is the rule for the function \(f\)?
- A. \(f(x) = \sqrt{5-4x}\)
- B. \(f(x) = -\sqrt{x-5}\)
- C. \(f(x) = \sqrt{x+5}\)
- D. \(f(x) = -\sqrt{4x-5}\)
- E. \(f(x) = -\sqrt{4x-10}\)
Consider the graphs of the functions \(f\) and \(g\) shown below.
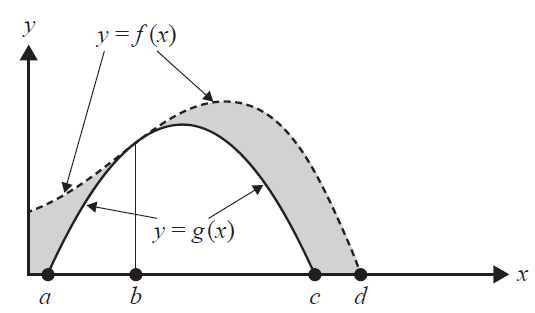
The area of the shaded region could be represented by
- A. \(\int_a^d (f(x)-g(x))dx\)
- B. \(\int_0^d (f(x)-g(x))dx\)
- C. \(\int_0^b (f(x)-g(x))dx + \int_b^c (f(x)-g(x))dx\)
- D. \(\int_0^a f(x)dx + \int_a^c (f(x)-g(x))dx+\int_b^d f(x)dx \)
- E. \(\int_0^d f(x)dx - \int_a^c g(x)dx\)
A rectangle is formed by using part of the coordinate axes and a point \((u, v)\), where \(u > 0\) on the parabola \(y = 4-x^2\).
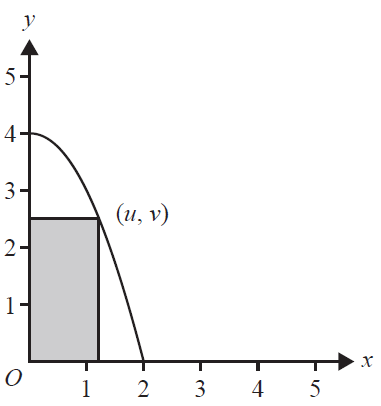
Which one of the following is the maximum area of the rectangle?
- A. 4
- B. \(\frac{2\sqrt{3}}{3}\)
- C. \(\frac{8\sqrt{3}-4}{3}\)
- D. \(\frac{8}{3}\)
- E. \(\frac{16\sqrt{3}}{9}\)
A box contains six red marbles and four blue marbles. Two marbles are drawn from the box, without replacement.
The probability that they are the same colour is
- A. \(\frac{1}{2}\)
- B. \(\frac{28}{45}\)
- C. \(\frac{7}{15}\)
- D. \(\frac{3}{5}\)
- E. \(\frac{1}{3}\)
The random variable, \(X\), has a normal distribution with mean 12 and standard deviation 0.25.
If the random variable, \(Z\), has the standard normal distribution, then the probability that \(X\) is greater than 12.5 is equal to
- A. \(\Pr(Z < -4)\)
- B. \(\Pr(Z < -1.5)\)
- C. \(\Pr(Z < 1)\)
- D. \(\Pr(Z \ge 1.5)\)
- E. \(\Pr(Z > 2)\)
Inside a container there are one million coloured building blocks. It is known that 20% of the blocks are red. A sample of 16 blocks is taken from the container. For samples of 16 blocks, \(\hat{P}\) is the random variable of the distribution of sample proportions of red blocks. (Do not use a normal approximation.)
\(\Pr(\hat{P} \ge \frac{3}{16})\) is closest to
- A. 0.6482
- B. 0.8593
- C. 0.7543
- D. 0.6542
- E. 0.3211
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
A company produces motors for refrigerators. There are two assembly lines, Line A and Line B. 5% of the motors assembled on Line A are faulty and 8% of the motors assembled on Line B are faulty. In one hour, 40 motors are produced from Line A and 50 motors are produced from Line B. At the end of an hour, one motor is selected at random from all the motors that have been produced during that hour.
a. What is the probability that the selected motor is faulty? Express your answer in the form \(\frac{1}{b}\), where \(b\) is a positive integer. 2 marks
b. The selected motor is found to be faulty. What is the probability that it was assembled on Line A? Express your answer in the form \(\frac{1}{c}\), where \(c\) is a positive integer. 1 mark
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

