2020 VCE Maths Methods Mini Test 5
Number of marks: 9
Reading time: 2 minutes
Writing time: 13 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
If \(\int_1^8 f(x)dx = 5\), then \(\int_0^2 f(2(x+2))dx\) is equal to
- A. 12
- B. 10
- C. 8
- D. \(\frac{1}{2}\)
- E. \(\frac{5}{2}\)
Given that \(\log_2(n+1) = x\), the values of \(n\) for which \(x\) is a positive integer are
- A. \(n = 2k, k \in Z^+\)
- B. \(n = 2^k - 1, k \in Z^+\)
- C. \(n = 2k - 1, k \in Z^+\)
- D. \(n = 2k-1, k \in Z^+\)
- E. \(n = 2k, k \in Z^+\)
The lengths of plastic pipes that are cut by a particular machine are a normally distributed random variable, \(X\), with a mean of 250 mm.
\(Z\) is the standard normal random variable.
If \(\Pr(X < 259) = 1 - \Pr(Z > 1.5)\), then the standard deviation of the lengths of plastic pipes, in millimetres, is
- A. 1.5
- B. 3
- C. 6
- D. 9
- E. 12
A clock has a minute hand that is 10 cm long and a clock face with a radius of 15 cm, as shown below.
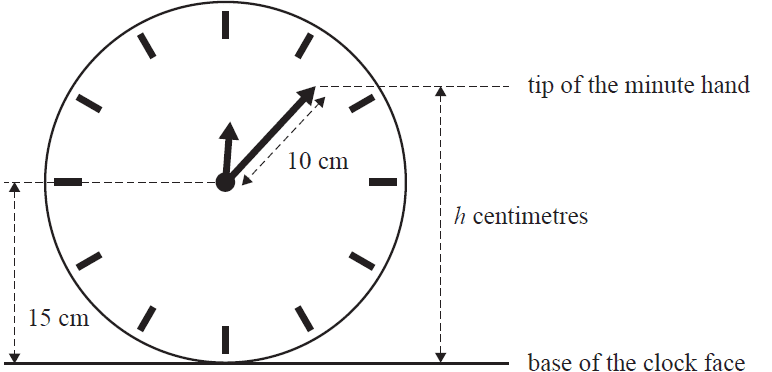
At 12.00 noon, both hands of the clock point vertically upwards and the tip of the minute hand is at its maximum distance above the base of the clock face.
The height, \(h\) centimetres, of the tip of the minute hand above the base of the clock face \(t\) minutes after 12.00 noon is given by
- A. \(h(t) = 15 + 10\sin\left(\frac{\pi t}{30}\right)\)
- B. \(h(t) = 15 - 10\sin\left(\frac{\pi t}{30}\right)\)
- C. \(h(t) = 15 + 10\sin\left(\frac{\pi t}{60}\right)\)
- D. \(h(t) = 15 + 10\cos\left(\frac{\pi t}{60}\right)\)
- E. \(h(t) = 15 + 10\cos\left(\frac{\pi t}{30}\right)\)
The random variable \(X\) is normally distributed.
The mean of \(X\) is twice the standard deviation of \(X\).
If \(\Pr(X > 5.2) = 0.9\), then the standard deviation of \(X\) is closest to
- A. 7.238
- B. 14.476
- C. 3.327
- D. 1.585
- E. 3.169
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
For a certain population the probability of a person being born with the specific gene SPGE1 is \(\frac{3}{5}\).
The probability of a person having this gene is independent of any other person in the population having this gene.
a. In a randomly selected group of four people, what is the probability that three or more people have the SPGE1 gene? 2 marks
b. In a randomly selected group of four people, what is the probability that exactly two people have the SPGE1 gene, given that at least one of those people has the SPGE1 gene? Express your answer in the form \(\frac{a^3}{b^4 - c^4}\), where \(a, b, c \in Z^+\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

