2021 VCE Maths Methods Mini Test 11
Number of marks: 8
Reading time: 1 minute
Writing time: 12 minutes
Section A – Calculator Allowed
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Which one of the following functions is differentiable for all real values of \(x\)?
- A. \( f(x) = \begin{cases} x & x < 0 \\ -x & x \ge 0 \end{cases} \)
- B. \( f(x) = \begin{cases} x & x < 0 \\ -x & x > 0 \end{cases} \)
- C. \( f(x) = \begin{cases} 8x+4 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
- D. \( f(x) = \begin{cases} 2x+1 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
- E. \( f(x) = \begin{cases} 4x+1 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
Let \(A\) and \(B\) be two independent events from a sample space.
If \(\Pr(A) = p\), \(\Pr(B) = p²\) and \(\Pr(A) + \Pr(B) = 1\), then \(\Pr(A' ∪ B)\) is equal to
- A. \(1 - p - p²\)
- B. \(p² - p³\)
- C. \(p - p³\)
- D. \(1 - p + p³\)
- E. \(1 - p - p² + p³\)
End of Section A
Section B – No Calculator
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Consider the unit circle \( x^2 + y^2 = 1 \) and the tangent to the circle at the point \(P\), shown in the diagram below.
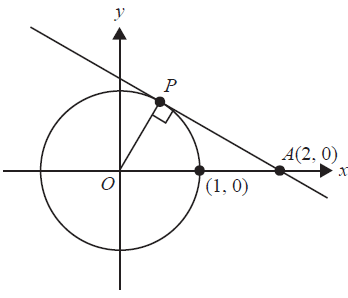
a. Show that the equation of the line that passes through the points \(A\) and \(P\) is given by \( y = -\frac{x}{\sqrt{3}} + \frac{2}{\sqrt{3}} \). 2 marks
b.No longer in curriculum
c. For \( 0 < q \le 1 \), let \(P'\) be the point of intersection of the graph of \(h\) with the unit circle, where \(P'\) is always the point of intersection that is closest to \(A\), as shown in the diagram below.
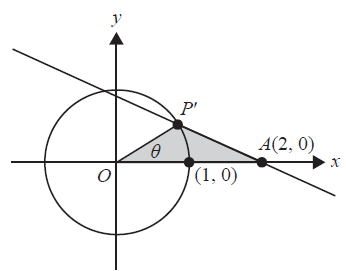
Let \(g\) be the function that gives the area of triangle \(OAP'\) in terms of \( \theta \).
i. Define the function \(g\). 2 marks
ii. Determine the maximum possible area of the triangle \(OAP'\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

