VCE Methods Integral Calculus Application Task 17

Question 1 [2018 Exam 2 Section B Q3]

A horizontal bridge positioned 5 m above level ground is 110 m in length. The bridge also touches the top of three arches. Each arch begins and ends at ground level. The arches are 5 m apart at the base, as shown in the diagram below.
Let \(x\) be the horizontal distance, in metres, from the left side of the bridge and let \(y\) be the height, in metres, above ground level.

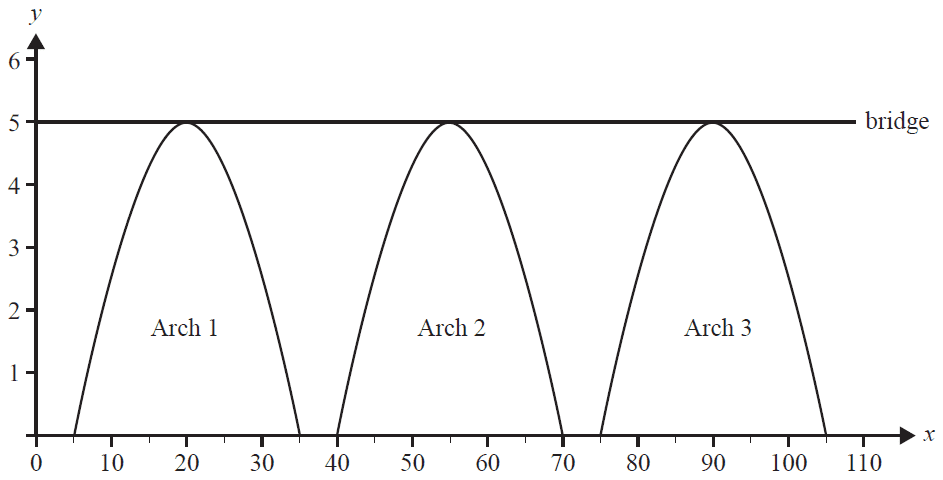
Arch 1 can be modelled by the function \( h_1 : [5, 35] \rightarrow \mathbb{R}, h_1(x) = 5\sin\left(\frac{(x-5)\pi}{30}\right) \).
Arch 2 can be modelled by the function \( h_2 : [40, 70] \rightarrow \mathbb{R}, h_2(x) = 5\sin\left(\frac{(x-40)\pi}{30}\right) \).
Arch 3 can be modelled by the function \( h_3 : [a, 105] \rightarrow \mathbb{R}, h_3(x) = 5\sin\left(\frac{(x-a)\pi}{30}\right) \).

a. State the value of \(a\), where \(a \in \mathbb{R}\). 1 mark

b. Describe the transformation that maps the graph of \(y = h_2(x)\) to \(y = h_3(x)\). 1 mark

The area above ground level between the arches and the bridge is filled with stone. The stone is represented by the shaded regions shown in the diagram below.

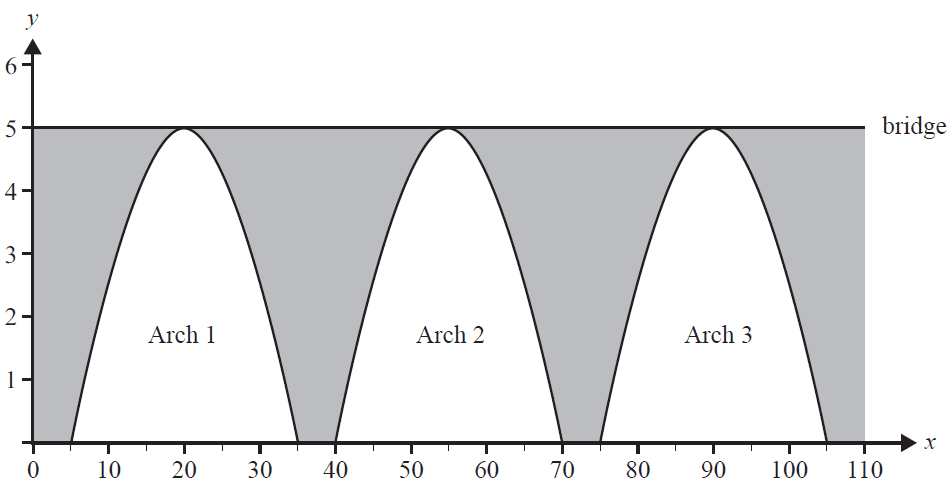
c. Find the total area of the shaded regions, correct to the nearest square metre. 3 marks

A second bridge has a height of 5 m above the ground at its left-most point and is inclined at a constant angle of elevation of \(\frac{\pi}{90}\) radians, as shown in the diagram below. The second bridge also has three arches below it, which are identical to the arches below the first bridge, and spans a horizontal distance of 110 m.
Let \(x\) be the horizontal distance, in metres, from the left side of the second bridge and let \(y\) be the height, in metres, above ground level.

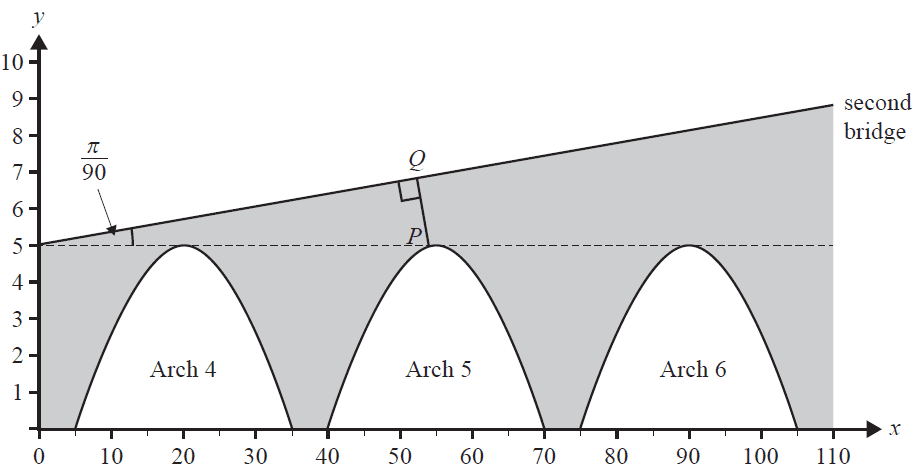
d. State the gradient of the second bridge, correct to three decimal places. 1 mark

e. \(P\) is a point on Arch 5. The tangent to Arch 5 at point \(P\) has the same gradient as the second bridge.
Find the coordinates of \(P\), correct to two decimal places. 2 marks

f. A supporting rod connects a point \(Q\) on the second bridge to point \(P\) on Arch 5. The rod follows a straight line and runs perpendicular to the second bridge, as shown in the diagram on page 18.
Find the distance \(PQ\), in metres, correct to two decimal places. 3 marks