VCE Methods Integral Calculus Application Task 12

Question 1 [2020 Exam 2 Section B Q4]

The graph of the function \(f(x) = 2xe^{1-x^2}\), where \(0 \le x \le 3\), is shown below.

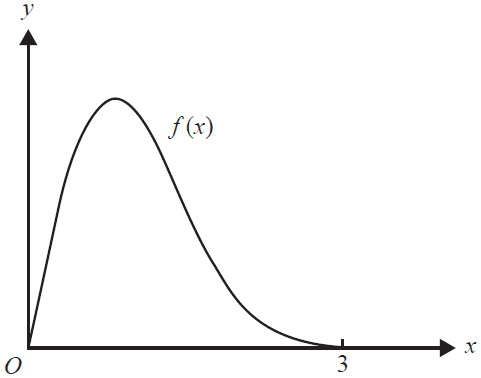
a. Find the slope of the tangent to \(f\) at \(x=1\). 1 mark

b. Find the obtuse angle that the tangent to \(f\) at \(x=1\) makes with the positive direction of the horizontal axis. Give your answer correct to the nearest degree. 1 mark

c. Find the slope of the tangent to \(f\) at a point \(x=p\). Give your answer in terms of \(p\). 1 mark

d.

i. Find the value of \(p\) for which the tangent to \(f\) at \(x=1\) and the tangent to \(f\) at \(x=p\) are perpendicular to each other. Give your answer correct to three decimal places. 2 marks

ii. Hence, find the coordinates of the point where the tangents to the graph of \(f\) at \(x=1\) and \(x=p\) intersect when they are perpendicular. Give your answer correct to two decimal places. 3 marks

Two line segments connect the points \((0, f(0))\) and \((3, f(3))\) to a single point \(Q(n, f(n))\), where \(1 < n < 3\), as shown in the graph below.

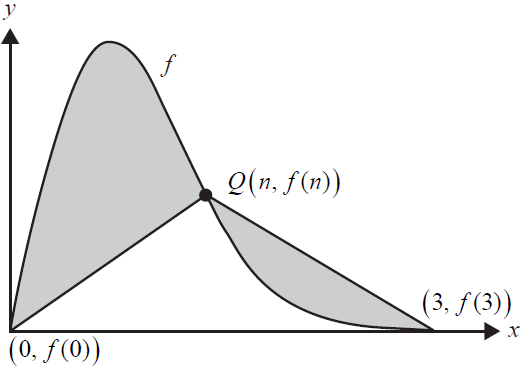
e.

i. The first line segment connects the point \((0, f(0))\) and the point \(Q(n, f(n))\), where \(1 < n < 3\).
Find the equation of this line segment in terms of \(n\). 1 mark

ii. The second line segment connects the point \(Q(n, f(n))\) and the point \((3, f(3))\), where \(1 < n < 3\).
Find the equation of this line segment in terms of \(n\). 1 mark

iii. Find the value of \(n\), where \(1 < n < 3\), if there are equal areas between the function \(f\) and each line segment. Give your answer correct to three decimal places. 3 marks