VCE Methods Integral Calculus Application Task 11

Question 1 [2020 Exam 2 Section B Q2]

An area of parkland has a river running through it, as shown below. The river is shown shaded.

The north bank of the river is modelled by the function \(f_1: [0, 200] \to \mathbb{R}\), \(f_1(x) = 20\cos\left(\frac{\pi x}{100}\right) + 40\).

The south bank of the river is modelled by the function \(f_2: [0, 200] \to \mathbb{R}\), \(f_2(x) = 20\cos\left(\frac{\pi x}{100}\right) + 30\).

The horizontal axis points east and the vertical axis points north.

All distances are measured in metres.

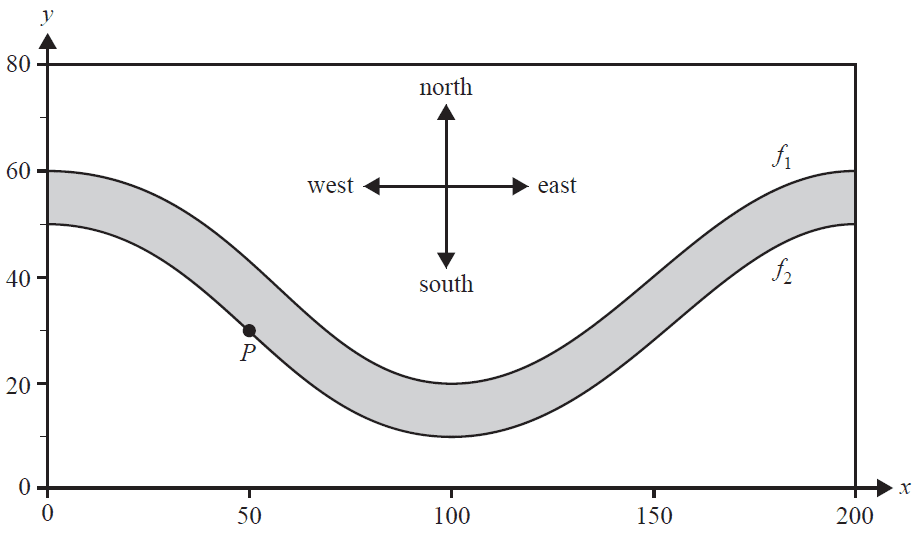
A swimmer always starts at point \(P\), which has coordinates \((50, 30)\).

Assume that no movement of water in the river affects the motion or path of the swimmer, which is always a straight line.

a. The swimmer swims north from point \(P\).
Find the distance, in metres, that the swimmer needs to swim to get to the north bank of the river. 1 mark

b. The swimmer swims east from point \(P\).
Find the distance, in metres, that the swimmer needs to swim to get to the north bank of the river. 2 marks

c. On another occasion, the swimmer swims the minimum distance from point \(P\) to the north bank of the river.
Find this minimum distance. Give your answer in metres, correct to one decimal place. 2 marks

d. Calculate the surface area of the section of the river shown on the graph on page 16, in square metres. 1 mark

e. A horizontal line is drawn through point \(P\). The section of the river that is south of the line is declared a ‘no swimming’ zone.
Find the area of the ‘no swimming’ zone, correct to the nearest square metre. 3 marks

f. Scientists observe that the north bank of the river is changing over time. It is moving further north from its current position. They model its predicted new location using the function with rule \(y = kf_1(x)\), where \(k \ge 1\).
Find the values of \(k\) for which the distance north across the river, for all parts of the river, is strictly less than 20 m. 2 marks