VCE Maths Methods Continuous Probability Mini Test 3
Number of marks: 9
Reading time: 2 minutes
Writing time: 13 minutes
Instructions – No Calculator
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
A random variable \(X\) has the probability density function \(f\) given by \( f(x) = \begin{cases} \frac{k}{x^2} & 1 \le x \le 2 \\ 0 & \text{elsewhere} \end{cases} \) where \(k\) is a positive real number.
a. Show that \(k = 2\). 1 mark
b. Find \(E(X)\). 2 marks
Let \(X\) be a continuous random variable with probability density function
\(f(x) = \begin{cases} -4x\log_e(x) & 0 < x \le 1 \\ 0 & \text{elsewhere} \end{cases} \)
Part of the graph of \(f\) is shown below. The graph has a turning point at \(x = \frac{1}{e}\).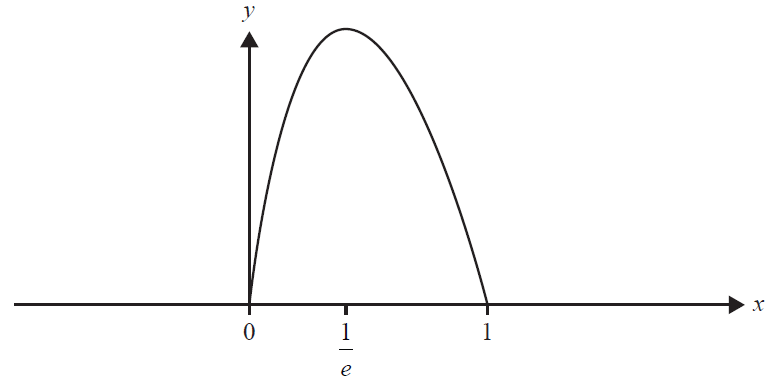
a. Show by differentiation that \(\frac{x^k}{k^2}(k\log_e(x)-1)\) is an antiderivative of \(x^{k-1}\log_e(x)\), where \(k\) is a positive real number. 2 marks
b.
i. Calculate \(\Pr(X > \frac{1}{e})\). 2 marks
ii. Hence, explain whether the median of \(X\) is greater than or less than \(\frac{1}{e}\), given that \(e > \frac{5}{2}\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

