2016 VCAA Maths Methods Exam 1
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 40
Reading time: 15 minutes
Writing time: 1 hours
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
a. Let \(y = \frac{\cos(x)}{x^2+2}\). Find \(\frac{dy}{dx}\). 2 marks
b. Let \(f(x) = x^2e^{5x}\). Evaluate \(f'(1)\). 2 marks
Let \(f: (-\infty, \frac{1}{2}] \to R\), where \(f(x) = \sqrt{1-2x}\).
a. Find \(f'(x)\). 1 mark
b. Find the angle \(\theta\) from the positive direction of the x-axis to the tangent to the graph of \(f\) at \(x = -1\), measured in the anticlockwise direction. 2 marks
Let \(f: R \setminus \{1\} \to R\), where \(f(x) = 2 + \frac{3}{x-1}\).
a. Sketch the graph of \(f\). Label the axis intercepts with their coordinates and label any asymptotes with the appropriate equation. 3 marks
b. Find the area enclosed by the graph of \(f\), the lines \(x=2\) and \(x=4\), and the x-axis. 2 marks
A paddock contains 10 tagged sheep and 20 untagged sheep. Four times each day, one sheep is selected at random from the paddock, placed in an observation area and studied, and then returned to the paddock.
a. What is the probability that the number of tagged sheep selected on a given day is zero? 1 mark
b. What is the probability that at least one tagged sheep is selected on a given day? 1 mark
c. What is the probability that no tagged sheep are selected on each of six consecutive days? Express your answer in the form \(\left(\frac{a}{b}\right)^c\), where \(a\), \(b\) and \(c\) are positive integers. 1 mark
Let \(f: (0, \infty) \to R\), where \(f(x) = \log_e(x)\) and \(g: R \to R\), where \(g(x) = x^2+1\).
a.
i. Find the rule for \(h\), where \(h(x) = f(g(x))\). 1 mark
ii. State the domain and range of \(h\). 2 marks
iii. Show that \(h(x) + h(-x) = f((g(x))^2)\). 2 marks
iv. Find the coordinates of the stationary point of \(h\) and state its nature. 2 marks
b. Let \(k: (-\infty, 0] \to R\), where \(k(x) = \log_e(x^2+1)\).
i. Find the rule for \(k^{-1}\). 2 marks
ii. State the domain and range of \(k^{-1}\). 2 marks
Let \(f: [-\pi, \pi] \to R\), where \(f(x) = 2\sin(2x) - 1\).
a. Calculate the average rate of change of \(f\) between \(x = -\frac{\pi}{3}\) and \(x = \frac{\pi}{6}\). 2 marks
b. Calculate the average value of \(f\) over the interval \(-\frac{\pi}{3} \le x \le \frac{\pi}{6}\). 3 marks
A company produces motors for refrigerators. There are two assembly lines, Line A and Line B. 5% of the motors assembled on Line A are faulty and 8% of the motors assembled on Line B are faulty. In one hour, 40 motors are produced from Line A and 50 motors are produced from Line B. At the end of an hour, one motor is selected at random from all the motors that have been produced during that hour.
a. What is the probability that the selected motor is faulty? Express your answer in the form \(\frac{1}{b}\), where \(b\) is a positive integer. 2 marks
b. The selected motor is found to be faulty. What is the probability that it was assembled on Line A? Express your answer in the form \(\frac{1}{c}\), where \(c\) is a positive integer. 1 mark
Let \(X\) be a continuous random variable with probability density function
\(f(x) = \begin{cases} -4x\log_e(x) & 0 < x \le 1 \\ 0 & \text{elsewhere} \end{cases} \)
Part of the graph of \(f\) is shown below. The graph has a turning point at \(x = \frac{1}{e}\).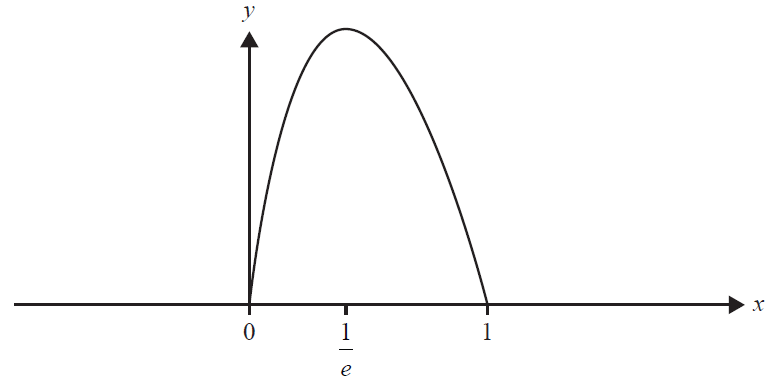
a. Show by differentiation that \(\frac{x^k}{k^2}(k\log_e(x)-1)\) is an antiderivative of \(x^{k-1}\log_e(x)\), where \(k\) is a positive real number. 2 marks
b.
i. Calculate \(\Pr(X > \frac{1}{e})\). 2 marks
ii. Hence, explain whether the median of \(X\) is greater than or less than \(\frac{1}{e}\), given that \(e > \frac{5}{2}\). 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

