2018 VCAA Maths Methods Exam 2

Question 1 [2018 Exam 2 Section A Q1]

Let \(f:R \to R\), \(f(x) = 4\cos\left(\frac{2\pi x}{3}\right) + 1\).

The period of this function is

• A. 1
• B. 2
• C. 3
• D. 4
• E. 5

Question 2 [2018 Exam 2 Section A Q2]

The maximal domain of the function \(f\) is \(R\setminus\{1\}\).

A possible rule for \(f\) is

• A. \(f(x) = \frac{x^2 - 5}{x-1}\)
• B. \(f(x) = \frac{x+4}{x-5}\)
• C. \(f(x) = \frac{x^2+x+4}{x^2+1}\)
• D. \(f(x) = \frac{5-x^2}{1+x}\)
• E. \(f(x) = \sqrt{x-1}\)

Question 3 [2018 Exam 2 Section A Q3]

Consider the function \(f:[a, b) \to R, f(x) = \frac{1}{x}\), where \(a\) and \(b\) are positive real numbers.

The range of \(f\) is

• A. \(\left[\frac{1}{a}, \frac{1}{b}\right)\)
• B. \(\left(\frac{1}{b}, \frac{1}{a}\right]\)
• C. \(\left[\frac{1}{b}, \frac{1}{a}\right)\)
• D. \(\left(\frac{1}{b}, \frac{1}{a}\right)\)
• E. \([a, b)\)

Question 4 [2018 Exam 2 Section A Q4]

The point \(A(3, 2)\) lies on the graph of the function \(f\). A transformation maps the graph of \(f\) to the graph of \(g\), where \(g(x) = \frac{1}{2}f(x-1)\). The same transformation maps the point \(A\) to the point \(P\).

The coordinates of the point \(P\) are

• A. \((2, 1)\)
• B. \((2, 4)\)
• C. \((4, 1)\)
• D. \((4, 2)\)
• E. \((4, 4)\)

Question 5 [2018 Exam 2 Section A Q5]

Consider \(f(x) = x^2 + \frac{p}{x}, x \neq 0, p \in R\).

There is a stationary point on the graph of \(f\) when \(x = -2\).

The value of \(p\) is

• A. \(-16\)
• B. \(-8\)
• C. \(2\)
• D. \(8\)
• E. \(16\)

Question 6 [2018 Exam 2 Section A Q6]

Let \(f\) and \(g\) be two functions such that \(f(x) = 2x\) and \(g(x+2) = 3x+1\).

The function \(f(g(x))\) is

• A. \(6x-5\)
• B. \(6x+1\)
• C. \(6x^2+1\)
• D. \(6x-10\)
• E. \(6x+2\)

Question 7 [2018 Exam 2 Section A Q7]

Let \(f: R^+ \to R, f(x) = k\log_2(x), k \in R\).

Given that \(f^{-1}(1) = 8\), the value of \(k\) is

• A. \(0\)
• B. \(\frac{1}{3}\)
• C. \(3\)
• D. \(8\)
• E. \(12\)

Question 8 [2018 Exam 2 Section A Q8]

If \(\int_1^{12} g(x)dx = 5\) and \(\int_{12}^{5} g(x)dx = -6\), then \(\int_1^{5} g(x)dx\) is equal to

• A. \(-11\)
• B. \(-1\)
• C. \(1\)
• D. \(3\)
• E. \(11\)

Question 9 [2018 Exam 2 Section A Q9]

A tangent to the graph of \(y = \log_e(2x)\) has a gradient of 2.

This tangent will cross the y-axis at

• A. \(0\)
• B. \(-0.5\)
• C. \(-1\)
• D. \(-1 - \log_e(2)\)
• E. \(-2\log_e(2)\)

Question 10 [2018 Exam 2 Section A Q10]

The function \(f\) has the property \(f(x + f(x)) = f(2x)\) for all non-zero real numbers \(x\).

Which one of the following is a possible rule for the function?

• A. \(f(x) = 1-x\)
• B. \(f(x) = x-1\)
• C. \(f(x) = x\)
• D. \(f(x) = \frac{x}{2}\)
• E. \(f(x) = \frac{1-x}{2}\)

Question 11 [2018 Exam 2 Section A Q11]

The graph of \(y = \tan(ax)\), where \(a \in R^+\), has a vertical asymptote \(x = 3\pi\) and has exactly one \(x\)-intercept in the region \((0, 3\pi)\).

The value of \(a\) is

• A. \(\frac{1}{6}\)
• B. \(\frac{1}{3}\)
• C. \(\frac{1}{2}\)
• D. \(1\)
• E. \(2\)

Question 12 [2018 Exam 2 Section A Q12]

The discrete random variable \(X\) has the following probability distribution.

\(x\)	0	1	2	3	6
\(\Pr(X=x)\)	\(\frac{1}{4}\)	\(\frac{9}{20}\)	\(\frac{1}{10}\)	\(\frac{1}{20}\)	\(\frac{3}{20}\)

Let \(\mu\) be the mean of \(X\).

\(\Pr(X < \mu)\) is

• A. \(\frac{1}{2}\)
• B. \(\frac{1}{4}\)
• C. \(\frac{17}{20}\)
• D. \(\frac{4}{5}\)
• E. \(\frac{7}{10}\)

Question 13 [2018 Exam 2 Section A Q13]

In a particular scoring game, there are two boxes of marbles and a player must randomly select one marble from each box. The first box contains four white marbles and two red marbles. The second box contains two white marbles and three red marbles. Each white marble scores \(-2\) points and each red marble scores \(+3\) points. The points obtained from the two marbles randomly selected by a player are added together to obtain a final score.

What is the probability that the final score will equal \(+1\)?

• A. \(\frac{2}{3}\)
• B. \(\frac{1}{5}\)
• C. \(\frac{2}{5}\)
• D. \(\frac{2}{15}\)
• E. \(\frac{8}{15}\)

Question 14 [2018 Exam 2 Section A Q14]

Two events, \(A\) and \(B\), are independent, where \(\Pr(B) = 2\Pr(A)\) and \(\Pr(A \cup B) = 0.52\)

\(\Pr(A)\) is equal to

• A. \(0.1\)
• B. \(0.2\)
• C. \(0.3\)
• D. \(0.4\)
• E. \(0.5\)

Question 15 [2018 Exam 2 Section A Q15]

A probability density function, \(f\), is given by

\( f(x) = \begin{cases} \frac{1}{12}(8x-x^3) & 0 \le x \le 2 \\ 0 & \text{elsewhere} \end{cases} \)

The median, \(m\), of this function satisfies the equation

• A. \(-m^4 + 16m^2 - 6 = 0\)
• B. \(-m^4 + 4m^2 - 6 = 0\)
• C. \(m^4 - 16m^2 = 0\)
• D. \(m^4 - 16m^2 + 24 = 0.5\)
• E. \(m^4 - 16m^2 + 24 = 0\)

Question 16 [2018 Exam 2 Section A Q16]

Jamie approximates the area between the \(x\)-axis and the graph of \(y = 2\cos(2x) + 3\), over the interval \(\left[0, \frac{\pi}{2}\right]\) using the three rectangles shown below.

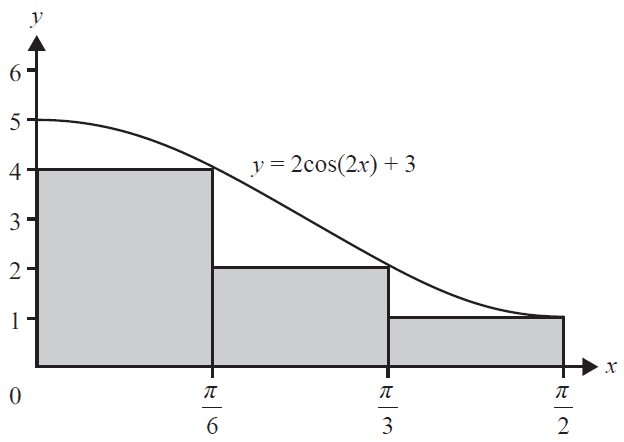
Jamie's approximation as a fraction of the exact area is

• A. \(\frac{5}{9}\)
• B. \(\frac{7}{9}\)
• C. \(\frac{9}{11}\)
• D. \(\frac{11}{18}\)
• E. \(\frac{7}{3}\)

Question 17 [2018 Exam 2 Section A Q17]

The turning point of the parabola \(y = x^2 - 2bx + 1\) is closest to the origin when

• A. \(b=0\)
• B. \(b = -1\) or \(b=1\)
• C. \(b = -\frac{1}{\sqrt{2}}\) or \(b = \frac{1}{\sqrt{2}}\)
• D. \(b = \frac{1}{2}\) or \(b = -\frac{1}{2}\)
• E. \(b = \frac{1}{4}\) or \(b = -\frac{1}{4}\)

Question 18 [2018 Exam 2 Section A Q18]

Consider the functions \(f:\mathbb{R}^+ \to \mathbb{R},\ f(x) = x^{\frac{p}{q}}\) and \(g:\mathbb{R}^+ \to \mathbb{R},\ g(x) = x^{\frac{m}{n}}\), where \(p, q, m\) and \(n\) are positive integers, and \(\frac{p}{q}\) and \(\frac{m}{n}\) are fractions in simplest form.

If \(\{x : f(x) > g(x)\} = (0, 1)\) and \(\{x : g(x) > f(x)\} = (1, \infty)\), which of the following must be false?

• A. \(q > n\) and \(p = m\)
• B. \(m > p\) and \(q = n\)
• C. \(pn < qm\)
• D. \(f'(c) = g'(c)\) for some \(c \in (0, 1)\)
• E. \(f'(d) = g'(d)\) for some \(d \in (1, \infty)\)

Question 19 [2018 Exam 2 Section A Q19]

The graphs \(f: R \to R, f(x) = \cos\left(\frac{\pi x}{2}\right)\) and \(g: R \to R, g(x) = \sin(\pi x)\) are shown in the diagram below.

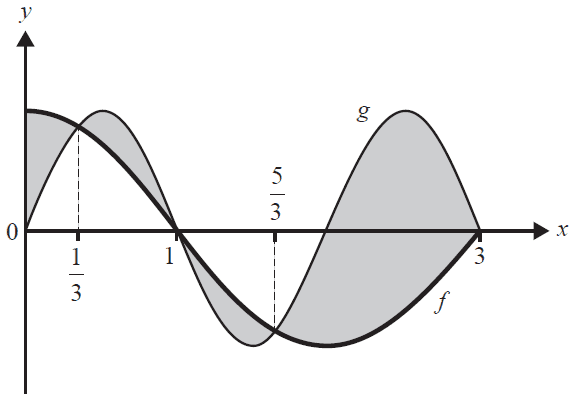
An integral expression that gives the total area of the shaded regions is

• A. \(\int_0^3 \left(\sin(\pi x) - \cos\left(\frac{\pi x}{2}\right)\right)dx\)
• B. \(2\int_\frac{5}{3}^{3} \left(\sin(\pi x) - \cos\left(\frac{\pi x}{2}\right)\right)dx\)
• C. \(\int_0^\frac{1}{3} \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx - 2\int_\frac{1}{3}^1 \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx - \int_\frac{5}{3}^3 \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx\)
• D. \(2\int_0^\frac{5}{3} \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx - 2\int_\frac{5}{3}^{3} \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx\)
• E. \(\int_0^\frac{1}{3} \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx + 2\int_\frac{1}{3}^1 \left(\sin(\pi x) - \cos\left(\frac{\pi x}{2}\right)\right)dx + \int_\frac{5}{3}^1 \left(\cos\left(\frac{\pi x}{2}\right) - \sin(\pi x)\right)dx\)

Question 20 [2018 Exam 2 Section A Q20]

The differentiable function \(f: R \to R\) is a probability density function. It is known that the median of the probability density function \(f\) is at \(x=0\) and \(f'(0) = 4\).

The transformation \(T: R^2 \to R^2\) maps the graph of \(f\) to the graph of \(g\), where \(g: R \to R\) is a probability density function with a median at \(x=0\) and \(g'(0) = -1\).

The transformation \(T\) could be given by

• A. \(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} -2 & 0 \\ 0 & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
• B. \(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 0 & -\frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
• C. \(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ \frac{1}{2} & 0 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
• D. \(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & 0 \\ -\frac{1}{2} & \frac{1}{2} \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)
• E. \(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} \frac{1}{2} & 0 \\ 0 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix}\)

Question 1 [2018 Exam 2 Section B Q1]

Consider the quartic \( f : \mathbb{R} \rightarrow \mathbb{R}, f(x) = 3x^4 + 4x^3 - 12x^2 \) and part of the graph of \(y = f(x)\) below.

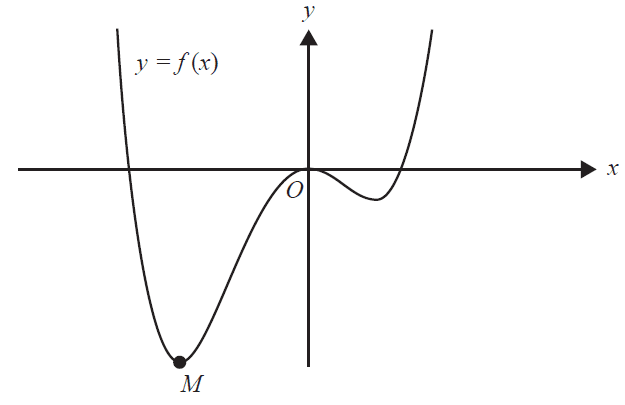
a. Find the coordinates of the point \(M\), at which the minimum value of the function \(f\) occurs. 1 mark

b. State the values of \(b \in \mathbb{R}\) for which the graph of \(y = f(x) + b\) has no x-intercepts. 1 mark

Part of the tangent, \(l\), to \(y = f(x)\) at \(x = -\frac{1}{3}\) is shown below.

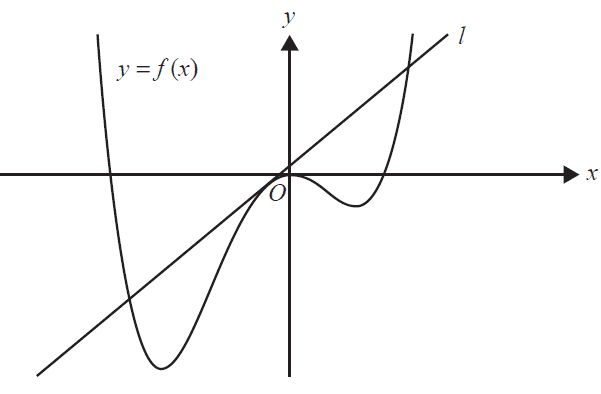
c. Find the equation of the tangent \(l\). 1 mark

d. The tangent \(l\) intersects \(y = f(x)\) at \(x = -\frac{1}{3}\) and at two other points.
State the x-values of the two other points of intersection. Express your answers in the form \(\frac{a \pm \sqrt{b}}{c}\), where \(a, b\) and \(c\) are integers. 2 marks

e. Find the total area of the regions bounded by the tangent \(l\) and \(y = f(x)\). Express your answer in the form \(\frac{a\sqrt{b}}{c}\), where \(a, b\) and \(c\) are positive integers. 2 marks

Let \( p : \mathbb{R} \rightarrow \mathbb{R}, p(x) = 3x^4 + 4x^3 + 6(a-2)x^2 - 12ax + a^2, a \in \mathbb{R} \).

f. State the value of \(a\) for which \(f(x) = p(x)\) for all \(x\). 1 mark

g. Find all solutions to \(p'(x) = 0\), in terms of \(a\) where appropriate. 1 mark

h.

i. Find the values of \(a\) for which \(p\) has only one stationary point. 1 mark

ii. Find the minimum value of \(p\) when \(a = 2\). 1 mark

iii. If \(p\) has only one stationary point, find the values of \(a\) for which \(p(x) = 0\) has no solutions. 2 marks

Question 2 [2018 Exam 2 Section B Q2]

A drug, X, comes in 500 milligram (mg) tablets.
The amount, \(b\), of drug X in the bloodstream, in milligrams, \(t\) hours after one tablet is consumed is given by the function

\( b(t) = \frac{4500}{7} \left( e^{(-\frac{t}{5})} - e^{(-\frac{9t}{10})} \right) \)

a. Find the time, in hours, it takes for drug X to reach a maximum amount in the bloodstream after one tablet is consumed. Express your answer in the form \(a \log_e(c)\), where \(a, c \in \mathbb{R}\). 2 marks

The graph of \(y = b(t)\) is shown below for \(0 \le t \le 6\).

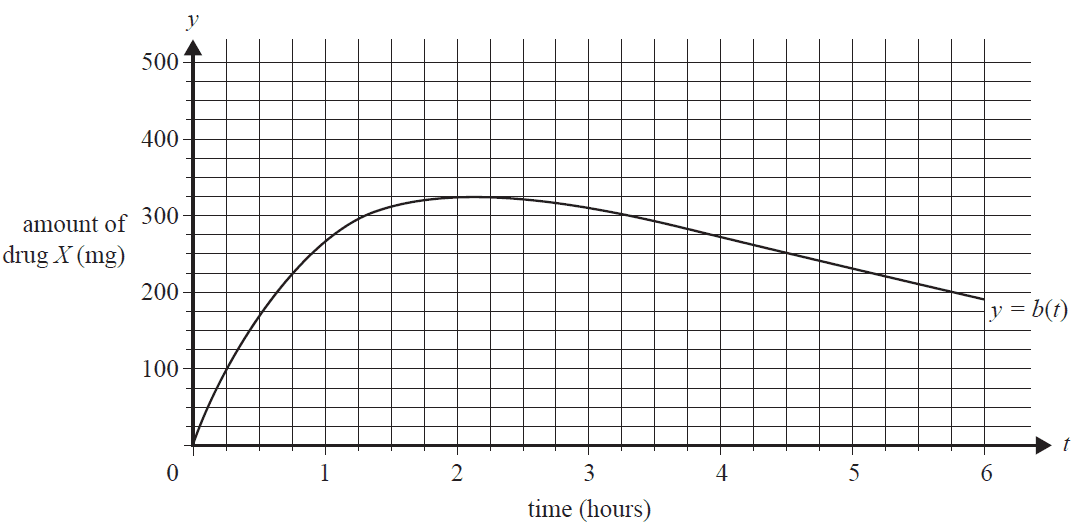
b. Find the average rate of change of the amount of drug X in the bloodstream, in milligrams per hour, over the interval [2, 6]. Give your answer correct to one decimal place. 2 marks

c. Find the average amount of drug X in the bloodstream, in milligrams, during the first six hours after one tablet is consumed. Give your answer correct to the nearest milligram. 2 marks

d. Six hours after one 500 milligram tablet of drug X is consumed (Tablet 1), a second identical tablet is consumed (Tablet 2). The amount of drug X in the bloodstream from each tablet consumed independently is shown in the graph below.

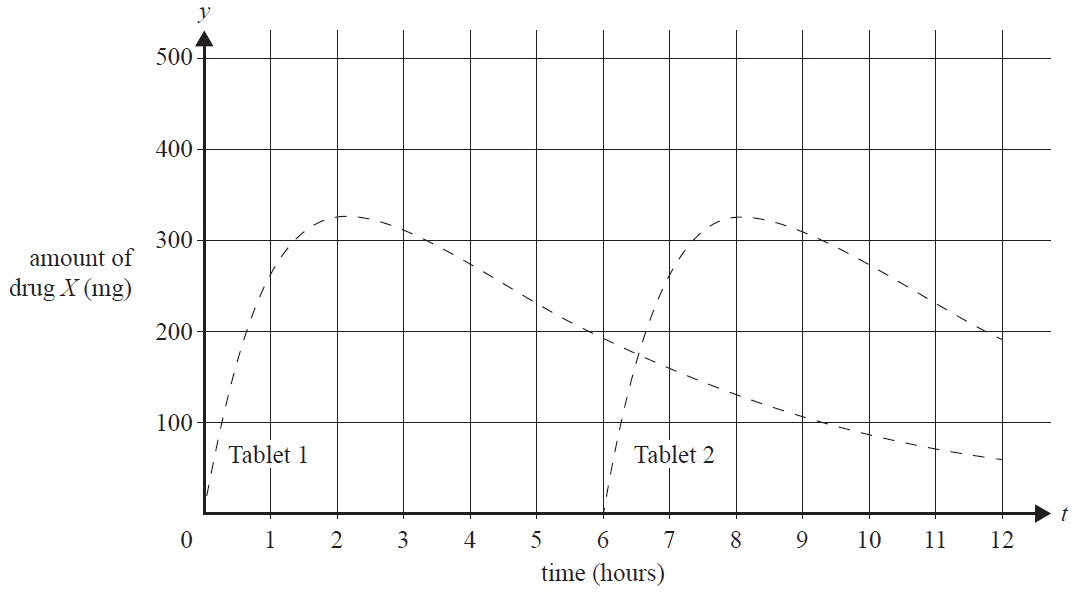
i. On the graph above, sketch the total amount of drug X in the bloodstream during the first 12 hours after Tablet 1 is consumed. 2 marks

ii. Find the maximum amount of drug X in the bloodstream in the first 12 hours and the time at which this maximum occurs. Give your answers correct to two decimal places. 2 marks

Question 3 [2018 Exam 2 Section B Q3]

A horizontal bridge positioned 5 m above level ground is 110 m in length. The bridge also touches the top of three arches. Each arch begins and ends at ground level. The arches are 5 m apart at the base, as shown in the diagram below.
Let \(x\) be the horizontal distance, in metres, from the left side of the bridge and let \(y\) be the height, in metres, above ground level.

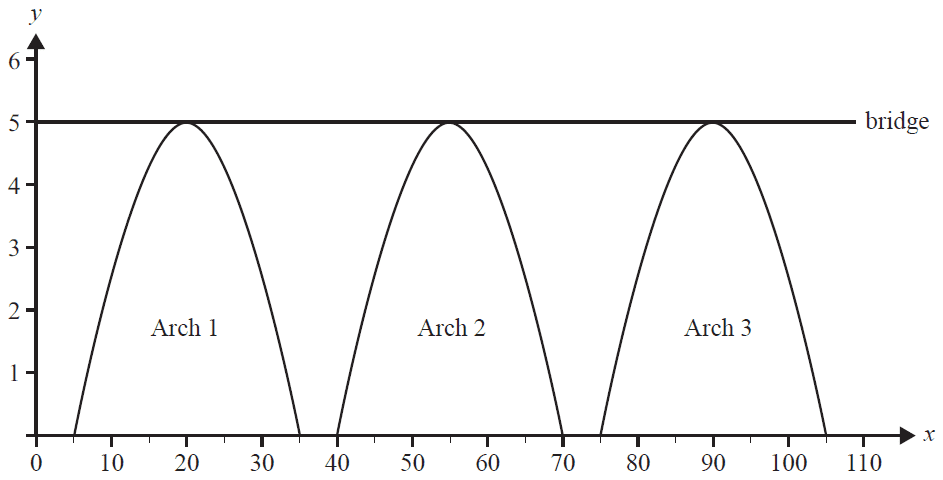
Arch 1 can be modelled by the function \( h_1 : [5, 35] \rightarrow \mathbb{R}, h_1(x) = 5\sin\left(\frac{(x-5)\pi}{30}\right) \).
Arch 2 can be modelled by the function \( h_2 : [40, 70] \rightarrow \mathbb{R}, h_2(x) = 5\sin\left(\frac{(x-40)\pi}{30}\right) \).
Arch 3 can be modelled by the function \( h_3 : [a, 105] \rightarrow \mathbb{R}, h_3(x) = 5\sin\left(\frac{(x-a)\pi}{30}\right) \).

a. State the value of \(a\), where \(a \in \mathbb{R}\). 1 mark

b. Describe the transformation that maps the graph of \(y = h_2(x)\) to \(y = h_3(x)\). 1 mark

The area above ground level between the arches and the bridge is filled with stone. The stone is represented by the shaded regions shown in the diagram below.

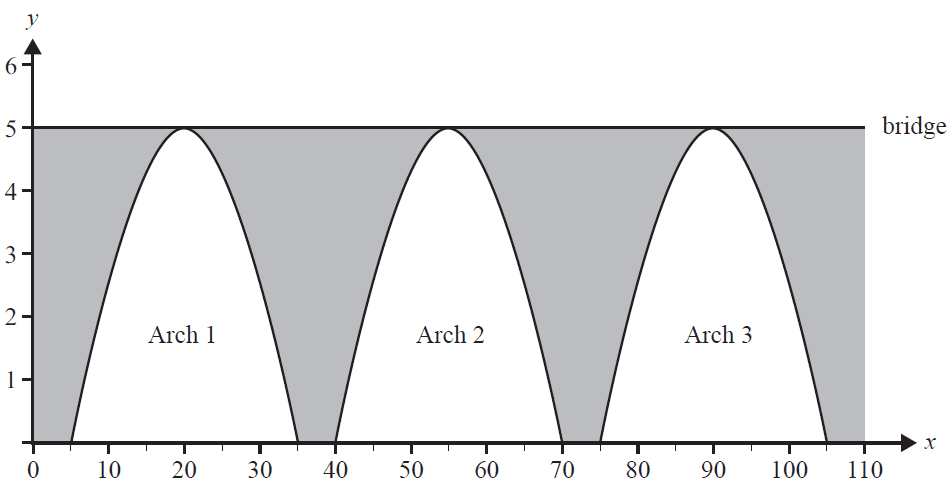
c. Find the total area of the shaded regions, correct to the nearest square metre. 3 marks

A second bridge has a height of 5 m above the ground at its left-most point and is inclined at a constant angle of elevation of \(\frac{\pi}{90}\) radians, as shown in the diagram below. The second bridge also has three arches below it, which are identical to the arches below the first bridge, and spans a horizontal distance of 110 m.
Let \(x\) be the horizontal distance, in metres, from the left side of the second bridge and let \(y\) be the height, in metres, above ground level.

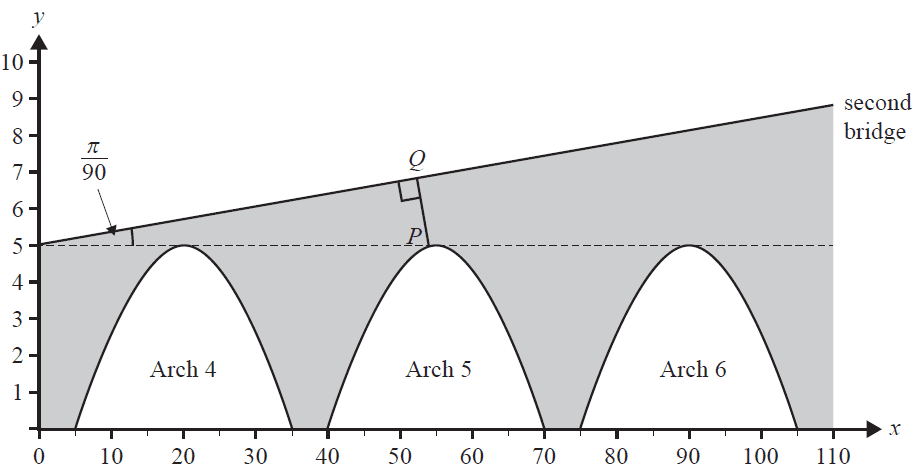
d. State the gradient of the second bridge, correct to three decimal places. 1 mark

e. \(P\) is a point on Arch 5. The tangent to Arch 5 at point \(P\) has the same gradient as the second bridge.
Find the coordinates of \(P\), correct to two decimal places. 2 marks

f. A supporting rod connects a point \(Q\) on the second bridge to point \(P\) on Arch 5. The rod follows a straight line and runs perpendicular to the second bridge, as shown in the diagram on page 18.
Find the distance \(PQ\), in metres, correct to two decimal places. 3 marks

Question 4 [2018 Exam 2 Section B Q4]

Doctors are studying the resting heart rate of adults in two neighbouring towns: Mathsland and Statsville. Resting heart rate is measured in beats per minute (bpm).
The resting heart rate of adults in Mathsland is known to be normally distributed with a mean of 68 bpm and a standard deviation of 8 bpm.

a. Find the probability that a randomly selected Mathsland adult has a resting heart rate between 60 bpm and 90 bpm. Give your answer correct to three decimal places. 1 mark

The doctors consider a person to have a slow heart rate if the person's resting heart rate is less than 60 bpm. The probability that a randomly chosen Mathsland adult has a slow heart rate is 0.1587.
It is known that 29% of Mathsland adults play sport regularly.
It is also known that 9% of Mathsland adults play sport regularly and have a slow heart rate.
Let \(S\) be the event that a randomly selected Mathsland adult plays sport regularly and let \(H\) be the event that a randomly selected Mathsland adult has a slow heart rate.

b.

i. Find \(\Pr(H|S)\), correct to three decimal places. 1 mark

ii. Are the events \(H\) and \(S\) independent? Justify your answer. 1 mark

c.

i. Find the probability that a random sample of 16 Mathsland adults will contain exactly one person with a slow heart rate. Give your answer correct to three decimal places. 2 marks

ii. For random samples of 16 Mathsland adults, \(\hat{P}\) is the random variable that represents the proportion of people who have a slow heart rate.
Find the probability that \(\hat{P}\) is greater than 10%, correct to three decimal places. 2 marks

iii. For random samples of \(n\) Mathsland adults, \(\hat{P}_n\) is the random variable that represents the proportion of people who have a slow heart rate.
Find the least value of \(n\) for which \(\Pr(\hat{P}_n > \frac{1}{n}) > 0.99\). 2 marks

The doctors took a large random sample of adults from the population of Statsville and calculated an approximate 95% confidence interval for the proportion of Statsville adults who have a slow heart rate. The confidence interval they obtained was (0.102, 0.145).

d.

i. Determine the sample proportion used in the calculation of this confidence interval. 1 mark

ii. Explain why this confidence interval suggests that the proportion of adults with a slow heart rate in Statsville could be different from the proportion in Mathsland. 1 mark

Every year at Mathsland Secondary College, students hike to the top of a hill that rises behind the school.
The time taken by a randomly selected student to reach the top of the hill has the probability density function \(M\) with the rule

\( M(t) = \begin{cases} \frac{3}{50} \left(\frac{t}{50}\right)^2 e^{-\left(\frac{t}{50}\right)^3} & t \ge 0 \\ 0 & t < 0 \end{cases} \)

where \(t\) is given in minutes.

e. Find the expected time, in minutes, for a randomly selected student from Mathsland Secondary College to reach the top of the hill. Give your answer correct to one decimal place. 2 marks

Students who take less than 15 minutes to get to the top of the hill are categorised as 'elite'.

f. Find the probability that a randomly selected student from Mathsland Secondary College is categorised as elite. Give your answer correct to four decimal places. 1 mark

g. The Year 12 students at Mathsland Secondary College make up \(\frac{1}{7}\) of the total number of students at the school. Of the Year 12 students at Mathsland Secondary College, 5% are categorised as elite.
Find the probability that a randomly selected non-Year 12 student at Mathsland Secondary College is categorised as elite. Give your answer correct to four decimal places. 2 marks

Question 5 [2018 Exam 2 Section B Q5]

Consider functions of the form

\( f : \mathbb{R} \rightarrow \mathbb{R}, f(x) = \frac{81x^2(a-x)}{4a^4} \)

and

\( h : \mathbb{R} \rightarrow \mathbb{R}, h(x) = \frac{9x}{2a^2} \)

where \(a\) is a positive real number.

a. Find the coordinates of the local maximum of \(f\) in terms of \(a\). 2 marks

b. Find the x-values of all of the points of intersection between the graphs of \(f\) and \(h\), in terms of \(a\) where appropriate. 1 mark

c. Determine the total area of the regions bounded by the graphs of \(y = f(x)\) and \(y = h(x)\). 2 marks

Consider the function \( g : \left[0, \frac{2a}{3}\right] \rightarrow \mathbb{R}, g(x) = \frac{81x^2(a-x)}{4a^4} \), where \(a\) is a positive real number.

d. Evaluate \(\frac{2a}{3} \times g\left(\frac{2a}{3}\right)\). 1 mark

e. Find the area bounded by the graph of \(g^{-1}\), the x-axis and the line \(x = g\left(\frac{2a}{3}\right)\). 2 marks

f. Find the value of \(a\) for which the graphs of \(g\) and \(g^{-1}\) have the same endpoints. 1 mark

g. Find the area enclosed by the graphs of \(g\) and \(g^{-1}\) when they have the same endpoints. 1 mark