2019 VCAA Maths Methods Exam 2

Question 1 [2019 Exam 2 Section A Q1]

Let \(f: R \to R, f(x) = 3\sin\left(\frac{2x}{5}\right) - 2\).
The period and range of \(f\) are respectively

• A. \(5\pi\) and \([-3, 3]\)
• B. \(5\pi\) and \([-5, 1]\)
• C. \(5\pi\) and \([-1, 5]\)
• D. \(\frac{5\pi}{2}\) and \([-5, 1]\)
• E. \(\frac{5\pi}{2}\) and \([-3, 3]\)

Question 2 [2019 Exam 2 Section A Q2]

The set of values of \(k\) for which \(x^2 + 2x - k = 0\) has two real solutions is

• A. \(\{-1, 1\}\)
• B. \((-1, \infty)\)
• C. \((-\infty, -1)\)
• D. \(\{-1\}\)
• E. \([-1, \infty)\)

Question 3 [2019 Exam 2 Section A Q3]

Let \(f: R\setminus\{4\} \to R, f(x) = \frac{a}{x-4}\), where \(a > 0\).
The average rate of change of \(f\) from \(x=6\) to \(x=8\) is

• A. \(a\log_e(2)\)
• B. \(\frac{a}{2}\log_e(2)\)
• C. \(2a\)
• D. \(-\frac{a}{4}\)
• E. \(-\frac{a}{8}\)

Question 4 [2019 Exam 2 Section A Q4]

\(\int_0^{\frac{\pi}{3}} (a\sin(x) + b\cos(x))dx\) is equal to

• A. \(\frac{(2-\sqrt{3})a-b}{2}\)


• B. \(\frac{b-(2-\sqrt{3})a}{2}\)


• C. \(\frac{(2-\sqrt{3})a+b}{2}\)


• D. \(\frac{(2-\sqrt{3})b-a}{2}\)


• E. \(\frac{(2-\sqrt{3})b+a}{2}\)

Question 5 [2019 Exam 2 Section A Q5]

Let \(f'(x) = 3x^2 - 2x\) such that \(f(4) = 0\).
The rule of \(f\) is

• A. \(f(x) = x^3 - x^2\)
• B. \(f(x) = x^3 - x^2 + 48\)
• C. \(f(x) = x^3 - x^2 - 48\)
• D. \(f(x) = 6x - 2\)
• E. \(f(x) = 6x - 24\)

Question 6 [2019 Exam 2 Section A Q6]

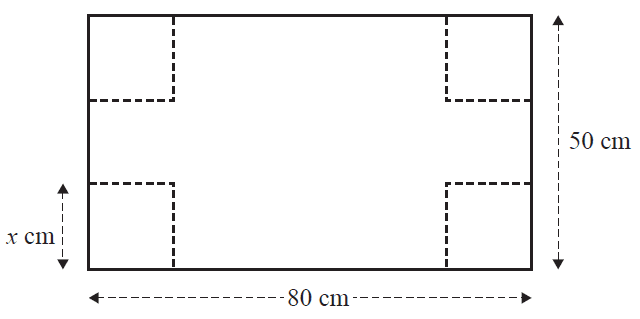
A rectangular sheet of cardboard has a length of 80 cm and a width of 50 cm. Squares, of side length \(x\) centimetres, are cut from each of the corners, as shown in the diagram below.

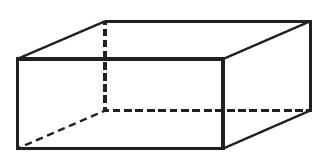
A rectangular box with an open top is then constructed, as shown in the diagram below.

The volume of the box is a maximum when \(x\) is equal to

• A. 10
• B. 20
• C. 25
• D. \(\frac{100}{3}\)
• E. \(\frac{200}{3}\)

Question 7 [2019 Exam 2 Section A Q7]

The discrete random variable \(X\) has the following probability distribution.

\(x\)	0	1	2	3
\(\Pr(X=x)\)	\(a\)	\(3a\)	\(5a\)	\(7a\)

The mean of \(X\) is

• A. \(\frac{1}{16}\)
• B. 1
• C. \(\frac{35}{16}\)
• D. \(\frac{17}{8}\)
• E. 2

Question 8 [2019 Exam 2 Section A Q8]

An archer can successfully hit a target with a probability of 0.9. The archer attempts to hit the target 80 times. The outcome of each attempt is independent of any other attempt.
Given that the archer successfully hits the target at least 70 times, the probability that the archer successfully hits the target exactly 74 times, correct to four decimal places, is

• A. 0.3635
• B. 0.8266
• C. 0.1494
• D. 0.3005
• E. 0.1701

Question 9 [2019 Exam 2 Section A Q9]

The point \((a, b)\) is transformed by

\(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} 1 \\ -2 \end{pmatrix}\)

If the image of \((a, b)\) is \((0, 0)\), then \((a, b)\) is

• A. (1, 1)
• B. (-1, 1)
• C. (-1, 0)
• D. (0, 1)
• E. (1, -1)

Question 10 [2019 Exam 2 Section A Q10]

Which one of the following statements is true for \(f: R \to R, f(x) = x + \sin(x)\)?

• A. The graph of \(f\) has a horizontal asymptote
• B. There are infinitely many solutions to \(f(x) = 4\)
• C. \(f\) has a period of \(2\pi\)
• D. \(f'(x) \ge 0\) for \(x \in R\)
• E. \(f'(x) = \cos(x)\)

Question 11 [2019 Exam 2 Section A Q11]

\(A\) and \(B\) are events from a sample space such that \(\Pr(A) = p\), where \(p > 0\), \(\Pr(B|A) = m\) and \(\Pr(B|A') = n\).
\(A\) and \(B\) are independent events when

• A. \(m = n\)
• B. \(m = 1-p\)
• C. \(m+n = 1\)
• D. \(m = p\)
• E. \(m+n = 1-p\)

Question 12 [2019 Exam 2 Section A Q12]

If \(\int_1^4 f(x)dx = 4\) and \(\int_2^4 f(x)dx = -2\), then \(\int_1^2 (f(x)+x)dx\) is equal to

• A. 2
• B. 6
• C. 8
• D. \(\frac{7}{2}\)
• E. \(\frac{15}{2}\)

Question 13 [2019 Exam 2 Section A Q13]

The graph of the function \(f\) passes through the point \((-2, 7)\).
If \(h(x) = f\left(\frac{x}{2}\right) + 5\), then the graph of the function \(h\) must pass through the point

• A. \((-1, -12)\)
• B. \((-1, 19)\)
• C. \((-4, 12)\)
• D. \((-4, -14)\)
• E. \((3, 3.5)\)

Question 14 [2019 Exam 2 Section A Q14]

The weights of packets of lollies are normally distributed with a mean of 200 g.
If 97% of these packets of lollies have a weight of more than 190 g, then the standard deviation of the distribution, correct to one decimal place, is

• A. 3.3 g
• B. 5.3 g
• C. 6.1 g
• D. 9.4 g
• E. 12.1 g

Question 15 [2019 Exam 2 Section A Q15]

Let \(f: [2, \infty) \to R, f(x) = x^2 - 4x + 2\) and \(f(5) = 7\). The function \(g\) is the inverse function of \(f\).
\(g'(7)\) is equal to

• A. \(\frac{1}{6}\)
• B. 5
• C. \(\frac{\sqrt{7}}{14}\)
• D. 6
• E. \(\frac{1}{7}\)

Question 16 [2019 Exam 2 Section A Q16]

Part of the graph of \(y = f(x)\) is shown below.

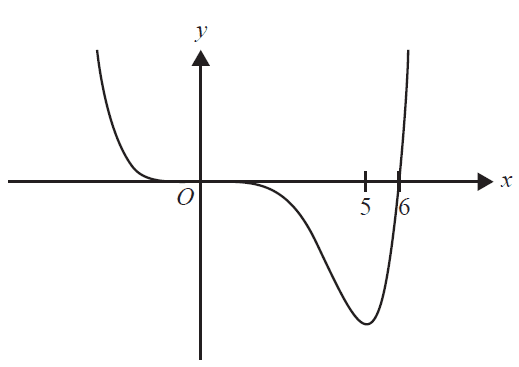
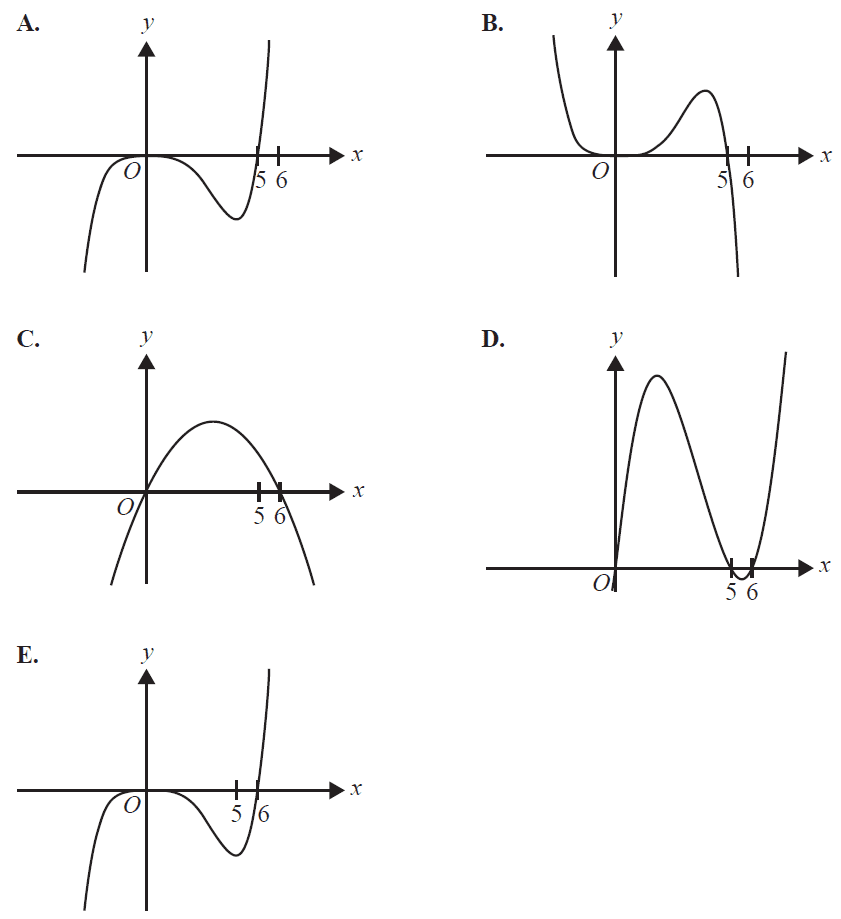
The corresponding part of the graph of \(y = f'(x)\) is best represented by

Question 17 [2019 Exam 2 Section A Q17]

A box contains \(n\) marbles that are identical in every way except colour, of which \(k\) marbles are coloured red and the remainder of the marbles are coloured green. Two marbles are drawn randomly from the box.
If the first marble is not replaced into the box before the second marble is drawn, then the probability that the two marbles drawn are the same colour is

• A. \(\frac{k^2 + (n-k)^2}{n^2}\)
• B. \(\frac{k^2 + (n-k-1)^2}{n^2}\)
• C. \(\frac{2k(n-k-1)}{n(n-1)}\)
• D. \(\frac{k(k-1) + (n-k)(n-k-1)}{n(n-1)}\)
• E. \(^nC_2\left(\frac{k}{n}\right)^2\left(1-\frac{k}{n}\right)^{n-2}\)

Question 18 [2019 Exam 2 Section A Q18]

The distribution of a continuous random variable, \(X\), is defined by the probability density function \(f\), where

\(f(x) = \begin{cases} p(x) & -a \le x \le b \\ 0 & \text{otherwise} \end{cases}\)

and \(a, b \in R^+\).
The graph of the function \(p\) is shown below.

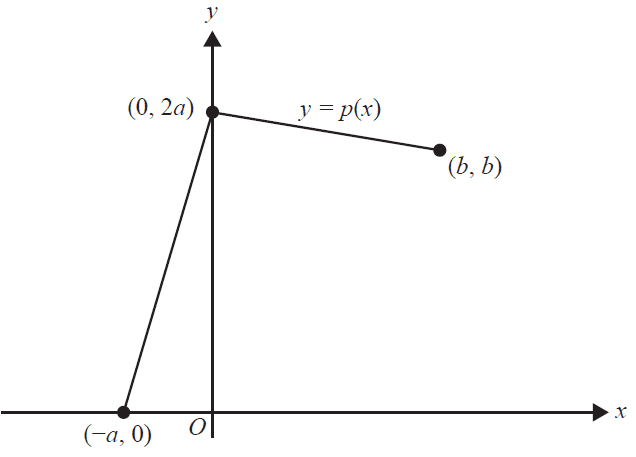
It is known that the average value of \(p\) over the interval \([-a, b]\) is \(\frac{3}{4}\).
\(\Pr(X>0)\) is

• A. \(\frac{2}{3}\)
• B. \(\frac{3}{4}\)
• C. \(\frac{4}{5}\)
• D. \(\frac{7}{9}\)
• E. \(\frac{5}{6}\)

Question 19 [2019 Exam 2 Section A Q19]

Given that \(\tan(a) = d\), where \(d > 0\) and \(0 < a < \frac{\pi}{2}\), the sum of the solutions to \(\tan(2x) = d\), where \(0 < x < \frac{5\pi}{4}\), in terms of \(a\), is

• A. 0
• B. \(2a\)
• C. \(\pi + 2a\)
• D. \(\frac{\pi}{2} + a\)
• E. \(\frac{3(\pi+a)}{2}\)

Question 20 [2019 Exam 2 Section A Q20]

The expression \(\log_x(y) + \log_y(z)\), where \(x, y\) and \(z\) are all real numbers greater than 1, is equal to

• A. \(-\frac{1}{\log_y(x)} - \frac{1}{\log_z(y)}\)
• B. \(\frac{1}{\log_x(y)} + \frac{1}{\log_y(z)}\)
• C. \(-\frac{1}{\log_x(y)} - \frac{1}{\log_y(z)}\)
• D. \(\frac{1}{\log_y(x)} + \frac{1}{\log_z(y)}\)
• E. \(\log_y(x) + \log_z(y)\)

Question 1 [2019 Exam 2 Section B Q1]

Let \(f: \mathbb{R} \to \mathbb{R}\), \(f(x) = x^2e^{-x^2}\).

a. Find \(f'(x)\). 1 mark

b.

i. State the nature of the stationary point on the graph of \(f\) at the origin. 1 mark

ii. Find the maximum value of the function \(f\) and the values of \(x\) for which the maximum occurs. 2 marks

iii. Find the values of \(d \in \mathbb{R}\) for which \(f(x) + d\) is always negative. 1 mark

c.

i. Find the equation of the tangent to the graph of \(f\) at \(x = -1\). 1 mark

ii. Find the area enclosed by the graph of \(f\) and the tangent to the graph of \(f\) at \(x = -1\), correct to four decimal places. 2 marks

d. Let \(M(m, n)\) be a point on the graph of \(f\), where \(m \in [0, 1]\).
Find the minimum distance between \(M\) and the point \((0, e)\), and the value of \(m\) for which this occurs, correct to three decimal places. 3 marks

Question 2 [2019 Exam 2 Section B Q2]

An amusement park is planning to build a zip-line above a hill on its property.
The hill is modelled by \(y = \frac{3x(x-30)^2}{2000}\), \(x \in [0, 30]\), where \(x\) is the horizontal distance, in metres, from an origin and \(y\) is the height, in metres, above this origin, as shown in the graph below.

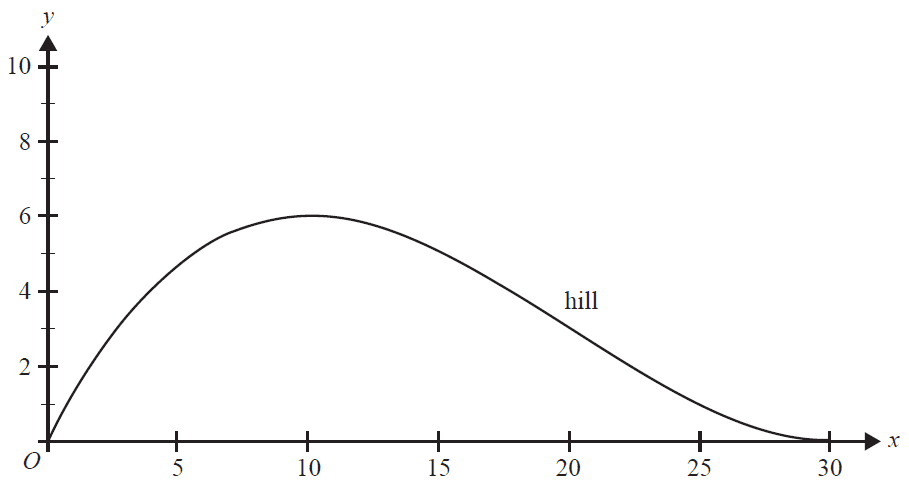
a. Find \(\frac{dy}{dx}\). 1 mark

b. State the set of values for which the gradient of the hill is strictly decreasing. 1 mark

The cable for the zip-line is connected to a pole at the origin at a height of 10 m and is straight for \(0 \le x \le a\), where \(10 \le a \le 20\). The straight section joins the curved section at \(A(a, b)\). The cable is then exactly 3 m vertically above the hill from \(a \le x \le 30\), as shown in the graph below.

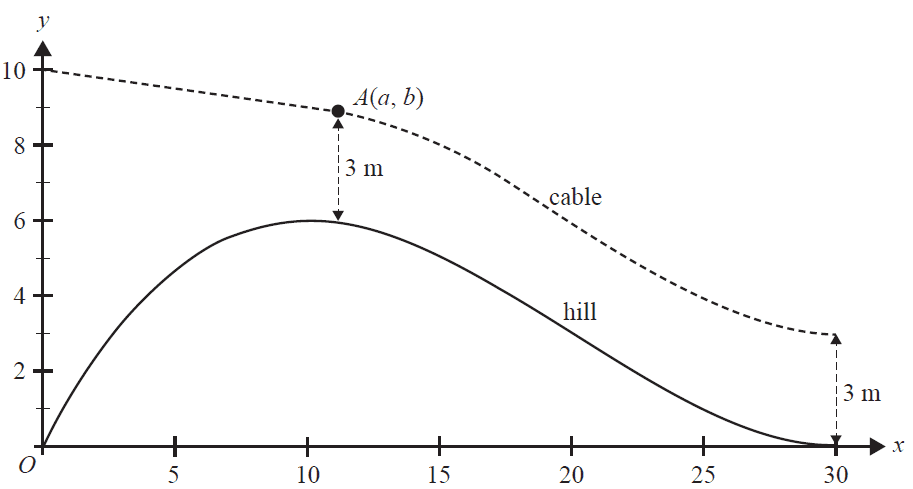
c. State the rule, in terms of \(x\), for the height of the cable above the horizontal axis for \(x \in [a, 30]\). 1 mark

d. Find the values of \(x\) for which the gradient of the cable is equal to the average gradient of the hill for \(x \in [10, 30]\). 3 marks

The gradients of the straight and curved sections of the cable approach the same value at \(x=a\), so there is a continuous and smooth join at \(A\).

e.

i. State the gradient of the cable at \(A\), in terms of \(a\). 1 mark

ii. Find the coordinates of \(A\), with each value correct to two decimal places. 3 marks

iii. Find the value of the gradient at \(A\), correct to one decimal place. 1 mark

Question 3 [2019 Exam 2 Section B Q3]

During a telephone call, a phone uses a dual-tone frequency electrical signal to communicate with the telephone exchange.
The strength, \(f\), of a simple dual-tone frequency signal is given by the function \(f(t) = \sin\left(\frac{\pi t}{3}\right) + \sin\left(\frac{\pi t}{6}\right)\) where \(t\) is a measure of time and \(t \ge 0\).
Part of the graph of \(y = f(t)\) is shown below.

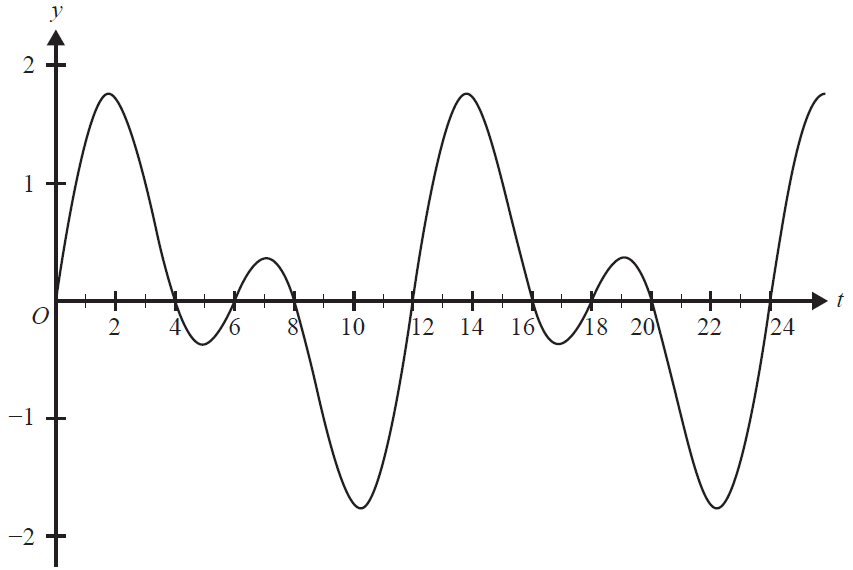
a. State the period of the function. 1 mark

b. Find the values of \(t\) where \(f(t) = 0\) for the interval \(t \in [0, 6]\). 1 mark

c. Find the maximum strength of the dual-tone frequency signal, correct to two decimal places. 1 mark

d. Find the area between the graph of \(f\) and the horizontal axis for \(t \in [0, 6]\). 2 marks

Let \(g\) be the function obtained by applying the transformation \(T\) to the function \(f\), where

\(T\begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} a & 0 \\ 0 & b \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} + \begin{pmatrix} c \\ d \end{pmatrix}\)

and \(a, b, c\) and \(d\) are real numbers.

e. Find the values of \(a, b, c\) and \(d\) given that \(\int_0^2 g(t)dt + \int_2^6 g(t)dt\) has the same area calculated in part d. 2 marks

f. The rectangle bounded by the line \(y=k\), \(k \in \mathbb{R}^+\), the horizontal axis, and the lines \(x=0\) and \(x=12\) has the same area as the area between the graph of \(f\) and the horizontal axis for one period of the dual-tone frequency signal.
Find the value of \(k\). 2 marks

Question 4 [2019 Exam 2 Section B Q4]

The Lorenz birdwing is the largest butterfly in Town A.
The probability density function that describes its life span, \(X\), in weeks, is given by

\(f(x) = \begin{cases} \frac{4}{625}(5x^3 - x^4) & 0 \le x \le 5 \\ 0 & \text{elsewhere} \end{cases}\)

a. Find the mean life span of the Lorenz birdwing butterfly. 2 marks

b. In a sample of 80 Lorenz birdwing butterflies, how many butterflies are expected to live longer than two weeks, correct to the nearest integer? 2 marks

c. What is the probability that a Lorenz birdwing butterfly lives for at least four weeks, given that it lives for at least two weeks, correct to four decimal places? 2 marks

The wingspans of Lorenz birdwing butterflies in Town A are normally distributed with a mean of 14.1 cm and a standard deviation of 2.1 cm.

d. Find the probability that a randomly selected Lorenz birdwing butterfly in Town A has a wingspan between 16 cm and 18 cm, correct to four decimal places. 1 mark

e. A Lorenz birdwing butterfly is considered to be very small if its wingspan is in the smallest 5% of all the Lorenz birdwing butterflies in Town A.
Find the greatest possible wingspan, in centimetres, for a very small Lorenz birdwing butterfly in Town A, correct to one decimal place. 1 mark

Each year, a detailed study is conducted on a random sample of 36 Lorenz birdwing butterflies in Town A.
A Lorenz birdwing butterfly is considered to be very large if its wingspan is greater than 17.5 cm. The probability that the wingspan of any Lorenz birdwing butterfly in Town A is greater than 17.5 cm is 0.0527, correct to four decimal places.

f.

i. Find the probability that three or more of the butterflies, in a random sample of 36 Lorenz birdwing butterflies from Town A, are very large, correct to four decimal places. 1 mark

ii. The probability that \(n\) or more butterflies, in a random sample of 36 Lorenz birdwing butterflies from Town A, are very large is less than 1%.
Find the smallest value of \(n\), where \(n\) is an integer. 2 marks

iii. For random samples of 36 Lorenz birdwing butterflies in Town A, \(\hat{P}\) is the random variable that represents the proportion of butterflies that are very large.
Find the expected value and the standard deviation of \(\hat{P}\), correct to four decimal places. 2 marks

iv. What is the probability that a sample proportion of butterflies that are very large lies within one standard deviation of 0.0527, correct to four decimal places? Do not use a normal approximation. 2 marks

g. The Lorenz birdwing butterfly also lives in Town B.
In a particular sample of Lorenz birdwing butterflies from Town B, an approximate 95% confidence interval for the proportion of butterflies that are very large was calculated to be \((0.0234, 0.0866)\), correct to four decimal places.
Determine the sample size used in the calculation of this confidence interval. 2 marks

Question 5 [2019 Exam 2 Section B Q5]

Let \(f: \mathbb{R} \to \mathbb{R}\), \(f(x) = 1 - x^3\). The tangent to the graph of \(f\) at \(x=a\), where \(0 < a < 1\), intersects the graph of \(f\) again at \(P\) and intersects the horizontal axis at \(Q\). The shaded regions shown in the diagram below are bounded by the graph of \(f\), its tangent at \(x=a\) and the horizontal axis.

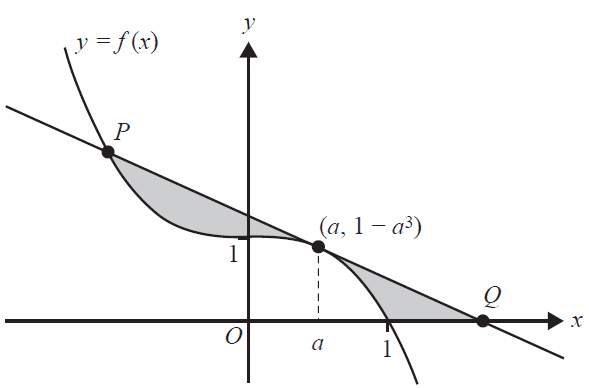
a. Find the equation of the tangent to the graph of \(f\) at \(x=a\), in terms of \(a\). 1 mark

b. Find the \(x\)-coordinate of \(Q\), in terms of \(a\). 1 mark

c. Find the \(x\)-coordinate of \(P\), in terms of \(a\). 2 marks

Let \(A\) be the function that determines the total area of the shaded regions.

d. Find the rule of \(A\), in terms of \(a\). 3 marks

e. Find the value of \(a\) for which \(A\) is a minimum. 2 marks

Consider the regions bounded by the graph of \(f^{-1}\), the tangent to the graph of \(f^{-1}\) at \(x=b\), where \(0 < b < 1\), and the vertical axis.

f. Find the value of \(b\) for which the total area of these regions is a minimum. 2 marks

g. Find the value of the acute angle between the tangent to the graph of \(f\) and the tangent to the graph of \(f^{-1}\) at \(x=1\). 1 mark