2021 VCAA Maths Methods Exam 2
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 80
Reading time: 15 minutes
Writing time: 2 hours
Section A – Multiple-choice questions
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The period of the function with rule \( y = \tan\left(\frac{\pi x}{2}\right) \) is
- A. 1
- B. 2
- C. 4
- D. 2π
- E. 4π
The graph of \( y = \log_e(x) + \log_e(2x) \), where \( x > 0 \), is identical, over the same domain, to the graph of
- A. \( y = 2\log_e\left(\frac{1}{2}x\right) \)
- B. \( y = 2\log_e(2x) \)
- C. \( y = \log_e(2x^2) \)
- D. \( y = \log_e(3x) \)
- E. \( y = \log_e(4x) \)
A box contains many coloured glass beads.
A random sample of 48 beads is selected and it is found that the proportion of blue-coloured beads in this sample is 0.125
Based on this sample, a 95% confidence interval for the proportion of blue-coloured glass beads is
- A. (0.0314, 0.2186)
- B. (0.0465, 0.2035)
- C. (0.0018, 0.2482)
- D. (0.0896, 0.1604)
- E. (0.0264, 0.2136)
The maximum value of the function \( h: [0, 2] \to R, h(x) = (x-2)e^x \) is
- A. \(-e\)
- B. 0
- C. 1
- D. 2
- E. \(e\)
Consider the following four functional relations.
\( f(x) = f(-x) \quad -f(x) = f(-x) \quad f(x) = -f(x) \quad (f(x))^2 = f(x^2) \)
The number of these functional relations that are satisfied by the function \( f: R \to R, f(x) = x \) is
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
The probability of winning a game is 0.25
The probability of winning a game is independent of winning any other game.
If Ben plays 10 games, the probability that he will win exactly four times is closest to
- A. 0.1460
- B. 0.2241
- C. 0.9219
- D. 0.0781
- E. 0.7759
The tangent to the graph of \( y = x^3 - ax^2 + 1 \) at \( x = 1 \) passes through the origin.
The value of \(a\) is
- A. \( \frac{1}{2} \)
- B. 1
- C. \( \frac{3}{2} \)
- D. 2
- E. \( \frac{5}{2} \)
The graph of the function \(f\) is shown below.
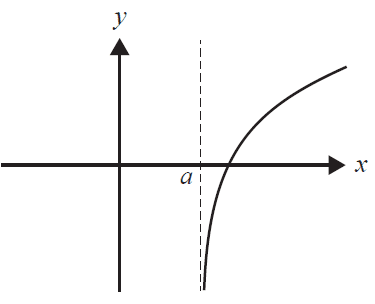
The graph corresponding to \(f'\) is
Let \( g(x) = x + 2 \) and \( f(x) = x^2 - 4 \).
If h is the composite function given by \( h: [-5, -1) \to R, h(x) = f(g(x)) \), then the range of \(h\) is
- A. (-3, 5]
- B. [-3, 5)
- C. (-3, 5)
- D. (-4, 5]
- E. [-4, 5]
Consider the functions \( f(x) = \sqrt{x+2} \) and \( g(x) = \sqrt{1-2x} \), defined over their maximal domains.
The maximal domain of the function \(h = f + g\) is
- A. \( \left[-2, \frac{1}{2}\right) \)
- B. \( [-2, \infty) \)
- C. \( (-\infty, -2] \cup \left[\frac{1}{2}, \infty\right) \)
- D. \( \left[-2, \frac{1}{2}\right] \)
- E. [-2, 1]
If \( \int_0^a f(x)dx = k \), then \( \int_0^a (3f(x) + 2)dx \) is
- A. \(3k + 2a\)
- B. \(3k\)
- C. \(k + 2a\)
- D. \(k + 2\)
- E. \(3k + 2\)
For a certain species of bird, the proportion of birds with a crest is known to be \( \frac{3}{5} \).
Let \( \hat{P} \) be the random variable representing the proportion of birds with a crest in samples of size \(n\) for this specific bird.
The smallest sample size for which the standard deviation of \( \hat{P} \) is less than 0.08 is
- A. 7
- B. 27
- C. 37
- D. 38
- E. 43
The value of an investment, in dollars, after n months can be modelled by the function
\( f(n) = 2500 \times (1.004)^n \)
where \( n \in \{0, 1, 2, ...\} \).
The average rate of change of the value of the investment over the first 12 months is closest to
- A. $10.00 per month.
- B. $10.20 per month.
- C. $10.50 per month.
- D. $125.00 per month.
- E. $127.00 per month.
A value of \(k\) for which the average value of \( y = \cos\left(kx - \frac{\pi}{2}\right) \) over the interval [0, π] is equal to the average value of \( y= \sin(x)\) over the same interval is
- A. \( \frac{1}{6} \)
- B. \( \frac{1}{5} \)
- C. \( \frac{1}{4} \)
- D. \( \frac{1}{3} \)
- E. \( \frac{1}{2} \)
Four fair coins are tossed at the same time.
The outcome for each coin is independent of the outcome for any other coin.
The probability that there is an equal number of heads and tails, given that there is at least one head, is
- A. \( \frac{1}{2} \)
- B. \( \frac{1}{3} \)
- C. \( \frac{3}{4} \)
- D. \( \frac{2}{5} \)
- E. \( \frac{4}{7} \)
Let \( \cos(x) = \frac{3}{5} \) and \( \sin^2(y) = \frac{25}{169} \), where \( x \in \left[\frac{3\pi}{2}, 2\pi\right] \) and \( y \in \left[\frac{3\pi}{2}, 2\pi\right] \).
The value of \(\sin(x) + \cos(y)\) is
- A. \( \frac{8}{65} \)
- B. \( -\frac{112}{65} \)
- C. \( \frac{112}{65} \)
- D. \( -\frac{8}{65} \)
- E. \( \frac{64}{65} \)
A discrete random variable \(X\) has a binomial distribution with a probability of success of \(p = 0.1\) for \(n\) trials, where \(n > 2\).
If the probability of obtaining at least two successes after \(n\) trials is at least 0.5, then the smallest possible value of \(n\) is
- A. 15
- B. 16
- C. 17
- D. 18
- E. 19
Let \( f: R \to R, f(x) = (2x-1)(2x+1)(3x-1) \) and \( g: (-\infty, 0) \to R, g(x) = x \log_e(-x) \).
The maximum number of solutions for the equation \( f(x-k) = g(x) \), where \( k \in R \), is
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
Which one of the following functions is differentiable for all real values of \(x\)?
- A. \( f(x) = \begin{cases} x & x < 0 \\ -x & x \ge 0 \end{cases} \)
- B. \( f(x) = \begin{cases} x & x < 0 \\ -x & x > 0 \end{cases} \)
- C. \( f(x) = \begin{cases} 8x+4 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
- D. \( f(x) = \begin{cases} 2x+1 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
- E. \( f(x) = \begin{cases} 4x+1 & x < 0 \\ (2x+1)^2 & x \ge 0 \end{cases} \)
Let \(A\) and \(B\) be two independent events from a sample space.
If \(\Pr(A) = p\), \(\Pr(B) = p²\) and \(\Pr(A) + \Pr(B) = 1\), then \(\Pr(A' ∪ B)\) is equal to
- A. \(1 - p - p²\)
- B. \(p² - p³\)
- C. \(p - p³\)
- D. \(1 - p + p³\)
- E. \(1 - p - p² + p³\)
End of Section A
Section B
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
A rectangular sheet of cardboard has a width of \(h\) centimetres. Its length is twice its width. Squares of side length \(x\) centimetres, where \(x > 0\), are cut from each of the corners, as shown in the diagram below.
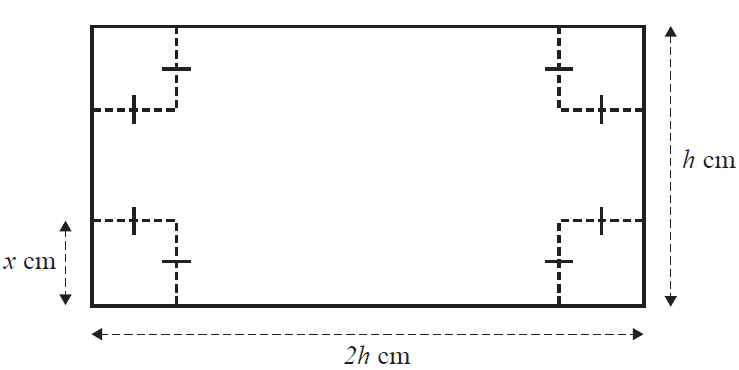
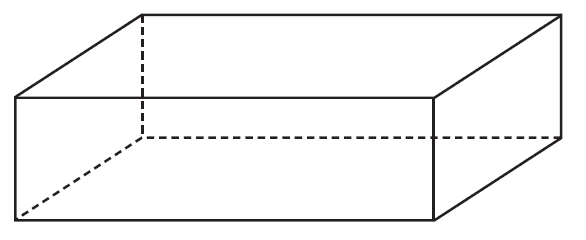
The sides of this sheet of cardboard are then folded up to make a rectangular box with an open top, as shown in the diagram below. Assume that the thickness of the cardboard is negligible and that \(V_{box} > 0\).
A box is to be made from a sheet of cardboard with \(h = 25\) cm.
a. Show that the volume, \(V_{box}\), in cubic centimetres, is given by \(V_{box}(x) = 2x(25 – 2x)(25 – x)\). 1 mark
b. State the domain of \(V_{box}\). 1 mark
c. Find the derivative of \(V_{box}\) with respect to \(x\). 1 mark
d. Calculate the maximum possible volume of the box and for which value of \(x\) this occurs. 3 marks
e. Waste minimisation is a goal when making cardboard boxes. Percentage wasted is based on the area of the sheet of cardboard that is cut out before the box is made. Find the percentage of the sheet of cardboard that is wasted when \(x = 5\). 2 marks
Now consider a box made from a rectangular sheet of cardboard where \(h > 0\) and the box's length is still twice its width.
f.
i. Let \(V_{box}\) be the function that gives the volume of the box. State the domain of \(V_{box}\) in terms of \(h\). 1 mark
ii. Find the maximum volume for any such rectangular box, \(V_{box}\), in terms of \(h\). 3 marks
g. Now consider making a box from a square sheet of cardboard with side lengths of \(h\) centimetres. Show that the maximum volume of the box occurs when \(x = \frac{h}{6}\). 2 marks
Four rectangles of equal width are drawn and used to approximate the area under the parabola \(y = x^2\) from \(x = 0\) to \(x = 1\). The heights of the rectangles are the values of the graph of \(y = x^2\) at the right endpoint of each rectangle, as shown in the graph below.
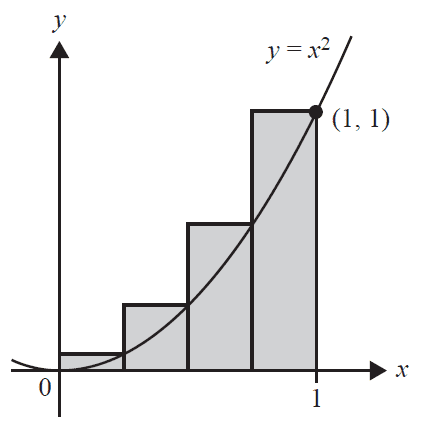
a. State the width of each of the rectangles shown above. 1 mark
b. Find the total area of the four rectangles shown above. 1 mark
c. Find the area between the graph of \(y = x^2\), the x-axis and the line \(x = 1\). 2 marks
d. The graph of \(f\) is shown below.
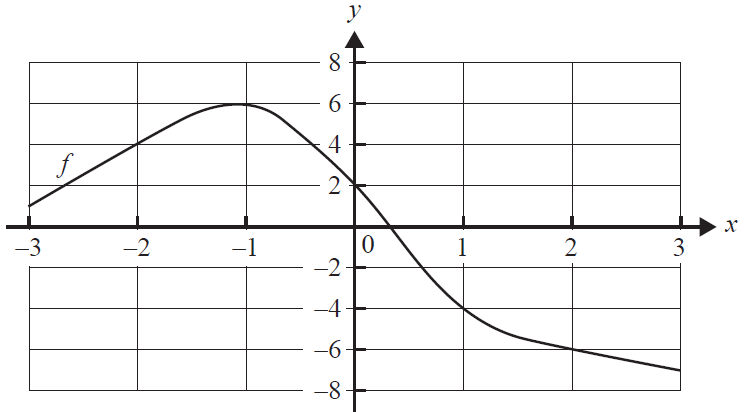
Approximate \(\int_{-2}^{2} f(x)dx\) using four rectangles of equal width and the right endpoint of each rectangle. 1 mark
e. Parts of the graphs of \(y = x^2\) and \(y = \sqrt{x}\) are shown below.
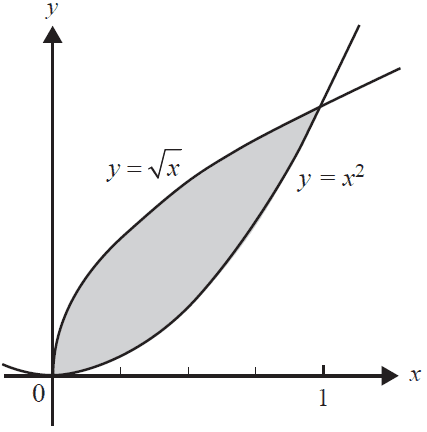
Find the area of the shaded region. 1 mark
f. The graph of \(y = x^2\) is transformed to the graph of \(y = ax^2\), where \(a \in (0, 2]\). Find the values of \(a\) such that the area defined by the region(s) bounded by the graphs of \(y = ax^2\) and \(y = \sqrt{x}\) and the lines \(x = 0\) and \(x = a\) is equal to \(\frac{1}{3}\). Give your answer correct to two decimal places. 4 marks
Let \(q(x) = \log_e(x^2 - 1) - \log_e(1 - x)\).
a. State the maximal domain and the range of \(q\). 2 marks
b.
i. Find the equation of the tangent to the graph of \(q\) when \(x = -2\). 1 mark
ii. Find the equation of the line that is perpendicular to the graph of \(q\) when \(x = -2\) and passes through the point \((-2, 0)\). 1 mark
Let \(p(x) = e^{-2x} - 2e^{-x} + 1\).
c. Explain why \(p\) is not a one-to-one function. 1 mark
d. Find the gradient of the tangent to the graph of \(p\) at \(x = a\). 1 mark
The diagram below shows parts of the graph of \(p\) and the line \(y = x + 2\).
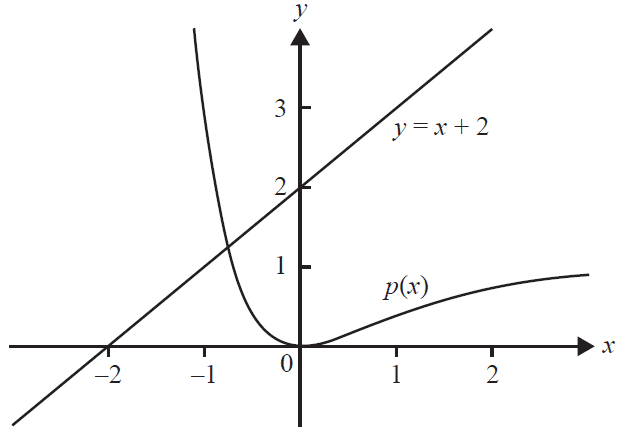
The line \(y = x + 2\) and the tangent to the graph of \(p\) at \(x = a\) intersect with an acute angle of \(\theta\) between them.
e. Find the value(s) of \(a\) for which \(\theta = 60^\circ\). Give your answer(s) correct to two decimal places. 3 marks
f. Find the x-coordinate of the point of intersection between the line \(y = x + 2\) and the graph of \(p\), and hence find the area bounded by \(y = x + 2\), the graph of \(p\) and the x-axis, both correct to three decimal places. 3 marks
A teacher coaches their school's table tennis team. The teacher has an adjustable ball machine that they use to help the players practise. The speed, measured in metres per second, of the balls shot by the ball machine is a normally distributed random variable \(W\). The teacher sets the ball machine with a mean speed of 10 metres per second and a standard deviation of 0.8 metres per second.
a. Determine \(\Pr(W \ge 11)\), correct to three decimal places. 1 mark
b. Find the value of \(k\), in metres per second, which 80% of ball speeds are below. Give your answer in metres per second, correct to one decimal place. 1 mark
The teacher adjusts the height setting for the ball machine. The machine now shoots balls high above the table tennis table. Unfortunately, with the new height setting, 8% of balls do not land on the table. Let \(\hat{P}\) be the random variable representing the sample proportion of balls that do not land on the table in random samples of 25 balls.
c. Find the mean and the standard deviation of \(\hat{P}\). 2 marks
d. Use the binomial distribution to find \(\Pr(\hat{P} > 0.1)\), correct to three decimal places. 2 marks
The teacher can also adjust the spin setting on the ball machine. The spin, measured in revolutions per second, is a continuous random variable \(X\) with the probability density function \[ f(x) = \begin{cases} \frac{x}{500} & 0 \le x < 20 \\ \frac{50-x}{750} & 20 \le x \le 50 \\ 0 & \text{elsewhere} \end{cases} \]
e. Find the maximum possible spin applied by the ball machine, in revolutions per second. 1 mark
f. Find the median spin, in revolutions per second, correct to one decimal place. 2 marks
g. Find the standard deviation of the spin, in revolutions per second, correct to one decimal place. 3 marks
h. The teacher adjusts the spin setting so that the median spin becomes 30 revolutions per second. This will transform the original probability density function \(f\) to a new probability density function \(g\), where \(g(x) = af(\frac{x}{b})\). Find the values of \(a\) and \(b\) for which the new median spin is 30 revolutions per second, giving your answer correct to two decimal places. 2 marks
Part of the graph of \(f: \mathbb{R} \rightarrow \mathbb{R}, f(x) = \sin(\frac{x}{2}) + \cos(2x)\) is shown below.
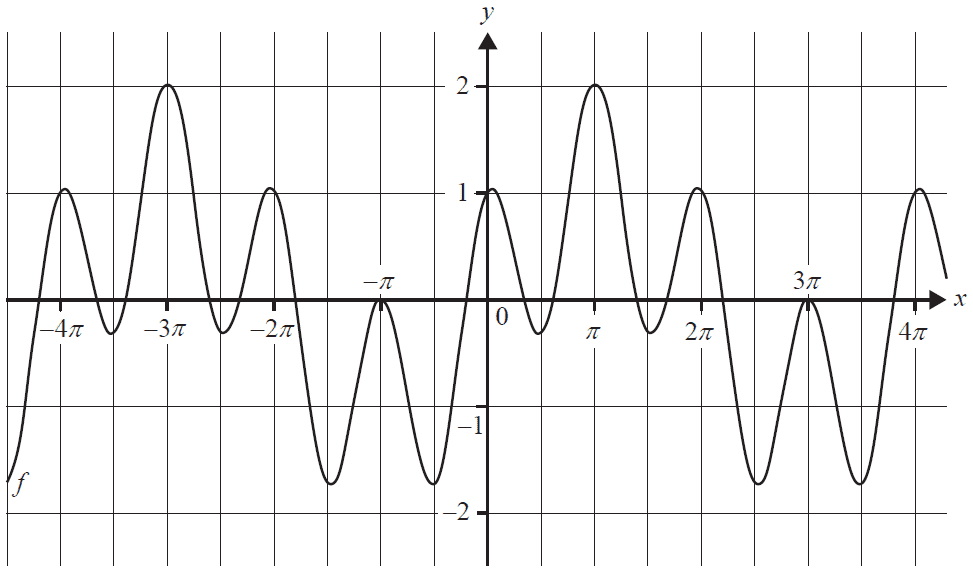
a. State the period of \(f\). 1 mark
b. State the minimum value of \(f\), correct to three decimal places. 1 mark
c. Find the smallest positive value of \(h\) for which \(f(h - x) = f(x)\). 1 mark
Consider the set of functions of the form \(g_a: \mathbb{R} \rightarrow \mathbb{R}, g_a(x) = \sin(\frac{x}{a}) + \cos(ax)\), where \(a\) is a positive integer.
d. State the value of \(a\) such that \(g_a(x) = f(x)\) for all \(x\). 1 mark
e.
i. Find an antiderivative of \(g_a\) in terms of \(a\). 1 mark
ii. Use a definite integral to show that the area bounded by \(g_a\) and the x-axis over the interval \([0, 2a\pi]\) is equal above and below the x-axis for all values of \(a\). 3 marks
f. Explain why the maximum value of \(g_a\) cannot be greater than 2 for all values of \(a\) and why the minimum value of \(g_a\) cannot be less than –2 for all values of \(a\). 1 mark
g. Find the greatest possible minimum value of \(g_a\). 1 mark
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au


