2022 VCAA Maths Methods Exam 2
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 80
Reading time: 15 minutes
Writing time: 2 hours
Section A – Multiple-choice questions
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The period of the function \( f(x) = 3\cos(2x + \pi) \) is
- A. \(2\pi\)
- B. \( \pi \)
- C. \( \frac{2\pi}{3} \)
- D. 2
- E. 3
The graph of \( y = \frac{1}{(x + 3)^2} + 4 \) has a horizontal asymptote with the equation
- A. \( y = 4 \)
- B. \( y = 3 \)
- C. \( y = 0 \)
- D. \( x = -2 \)
- E. \( x = -3 \)
The gradient of the graph of \( y = e^{3x} \) at the point where the graph crosses the vertical axis is equal to
- A. 0
- B. \( \frac{1}{e} \)
- C. 1
- D. e
- E. 3
Which one of the following functions is not continuous over the interval \( x \in [0, 5] \)?
- A. \( f(x) = \frac{1}{(x + 3)^2} \)
- B. \( f(x) = \sqrt{x + 3} \)
- C. \( f(x) = x^\frac{1}{3} \)
- D. \( f(x) = \tan\left(\frac{x}{3}\right) \)
- E. \( f(x) = \sin^2\left(\frac{x}{3}\right) \)
The largest value of \( a \) such that the function \( f : (-\infty, a] \to \mathbb{R}, f(x) = x^2 + 3x - 10 \), where \( f \) is one-to-one, is
- A. –12.25
- B. –5
- C. –1.5
- D. 0
- E. 2
Which of the pairs of functions below are not inverse functions?
- A. \( \begin{cases} f(x) = 5x + 3 \quad x \in \mathbb{R} \\ g(x) = \frac{x - 3}{5} \quad x \in \mathbb{R} \end{cases} \)
- B. \( \begin{cases} f(x) = \frac{2}{3}x + 2 \quad x \in \mathbb{R} \\ g(x) = \frac{3}{2}x - 3 \quad x \in \mathbb{R} \end{cases} \)
- C. \( \begin{cases} f(x) = x^2 \quad x < 0 \\ g(x) = \sqrt{x} \quad x > 0 \end{cases} \)
- D. \( \begin{cases} f(x) = \frac{1}{x} \quad x \ne 0 \\ g(x) = \frac{1}{x} \quad x \ne 0 \end{cases} \)
- E. \( \begin{cases} f(x) = \log_e(x) + 1 \quad x > 0 \\ g(x) = e^{x - 1} \quad x \in \mathbb{R} \end{cases} \)
The graph of \( y = f(x) \) is shown below.
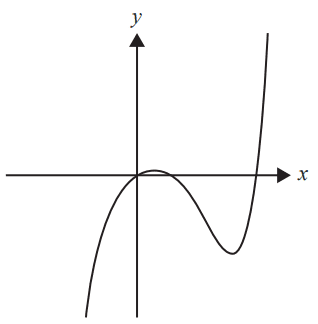
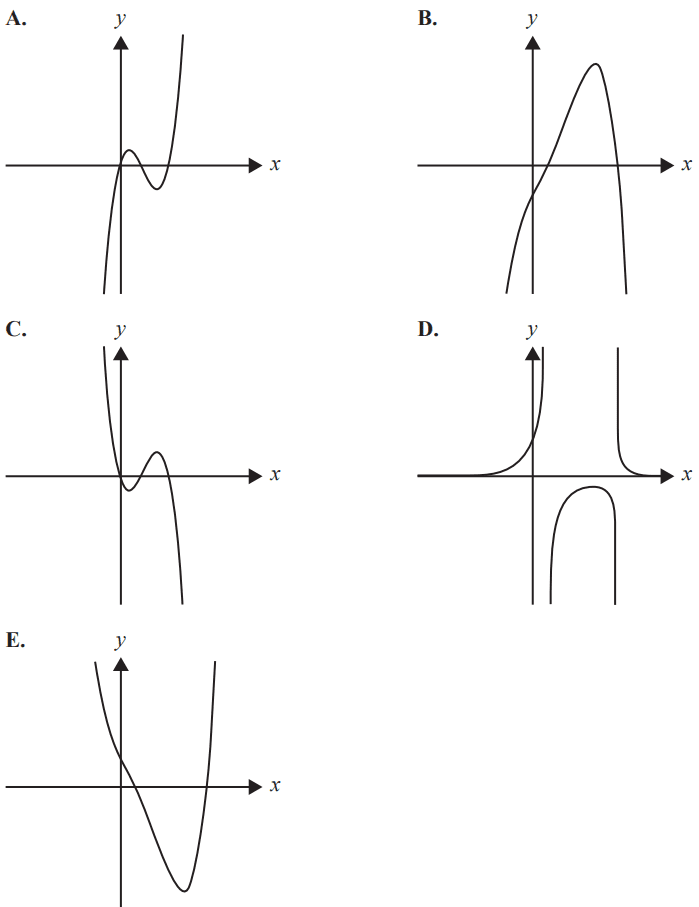
The graph of \( y = f'(x) \), the first derivative of \( f(x) \) with respect to \( x \), could be
If \( \int_0^b f(x)\,dx = 10 \) and \( \int_0^a f(x)\,dx = -4 \), where \( 0 < a < b \), then \( \int_a^b f(x)\,dx \) is equal to
- A. –6
- B. –4
- C. 0
- D. 10
- E. 14
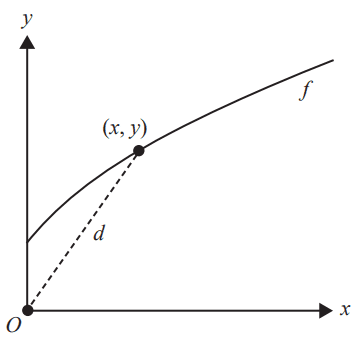
Let \( f : [0, \infty) \to \mathbb{R}, \ f(x) = \sqrt{2x + 1} \).
The shortest distance, \( d \), from the origin to the point \( (x, y) \) on the graph of \( f \) is given by
- A. \( d = x^2 + 2x + 1 \)
- B. \( d = x^2 + \sqrt{2x + 1} \)
- C. \( d = \sqrt{x^2 - 2x + 1} \)
- D. \( d = x + 1 \)
- E. \( d = 2x + 1 \)
An organisation randomly surveyed 1000 Australian adults and found that 55% of those surveyed were happy with their level of physical activity.
An approximate 95% confidence interval for the percentage of Australian adults who were happy with their level of physical activity is closest to
- A. (4.1, 6.9)
- B. (50.9, 59.1)
- C. (52.4, 57.6)
- D. (51.9, 58.1)
- E. (45.2, 64.8)
If \( \frac{d}{dx} \left( x \cdot \sin(x) \right) = \sin(x) + x \cdot \cos(x) \), then \( \frac{1}{k} \int x \cos(x)\, dx \) is equal to
- A. \( k \left( x \cdot \sin(x) - \int \sin(x)\, dx \right) + c \)
- B. \( \frac{1}{k} \cdot x \cdot \sin(x) - \int \sin(x)\, dx + c \)
- C. \( \frac{1}{k} \left( x \cdot \sin(x) - \int \sin(x)\, dx \right) + c \)
- D. \( \frac{1}{k} (x \cdot \sin(x) - \sin(x)) + c \)
- E. \( \frac{1}{k} \left( \int x \cdot \sin(x)\, dx - \int \sin(x)\, dx \right) + c \)
A bag contains three red pens and \( x \) black pens. Two pens are randomly drawn from the bag without replacement.
The probability of drawing a pen of each colour is equal to
- A. \( \frac{6x}{(2 + x)(3 + x)} \)
- B. \( \frac{3x}{(2 + x)(3 + x)} \)
- C. \( \frac{x}{2 + x} \)
- D. \( \frac{3 + x}{(2 + x)(3 + x)} \)
- E. \( \frac{3 + x}{5 + 2x} \)
The function \( f(x) = \log\left(\frac{a + x}{a - x}\right) \), where \( a \) is a positive real constant, has the maximal domain
- A. [–a, a]
- B. (–a, a)
- C. \( \mathbb{R} \setminus [–a, a] \)
- D. \( \mathbb{R} \setminus (–a, a) \)
- E. \( \mathbb{R} \)
A continuous random variable, \( X \), has a probability density function given by
\[ f(x) = \begin{cases} \frac{2}{9}x e^{-\frac{1}{9}x^2}, & x \geq 0 \\ 0, & x < 0 \end{cases} \]
The expected value of \( X \), correct to three decimal places, is
- A. 1.000
- B. 2.659
- C. 3.730
- D. 6.341
- E. 9.000
The maximal domain of the function with rule \( f(x) = \sqrt{x^2 - 2x - 3} \) is given by
- A. \( (-\infty, \infty) \)
- B. \( (-\infty, -3) \cup (3, \infty) \)
- C. \( (-1, 3) \)
- D. [–3, 1]
- E. \( (-\infty, -1] \cup [3, \infty) \)
The function \( f(x) = \frac{1}{3}x^3 + mx^2 + nx + p \), for \( m, n, p \in \mathbb{R} \), has turning points at \( x = -3 \) and \( x = 1 \) and passes through the point (3, 4).
The values of \( m, n \) and \( p \) respectively are
- A. \( m = 0, n = -\frac{7}{3}, p = 2 \)
- B. \( m = 1, n = -3, p = -5 \)
- C. \( m = -1, n = -3, p = 13 \)
- D. \( m = \frac{5}{4}, n = \frac{3}{2}, p = -\frac{83}{4} \)
- E. \( m = \frac{5}{2}, n = 6, p = -\frac{91}{2} \)
A function \( g \) is continuous on the domain \( x \in [a, b] \) and has the following properties:
• The average rate of change of \( g \) between \( x = a \) and \( x = b \) is positive.
• The instantaneous rate of change of \( g \) at \( x = \frac{a + b}{2} \) is negative.
Therefore, on the interval \( x \in [a, b] \), the function must be
- A. many-to-one
- B. one-to-many
- C. one-to-one
- D. strictly decreasing
- E. strictly increasing
If \( X \) is a binomial random variable where \( n = 20, p = 0.88 \), and \( \Pr(X \geq 16 \mid X \geq a) = 0.9175 \), correct to four decimal places, then \( a \) is equal to
- A. 11
- B. 12
- C. 13
- D. 14
- E. 15
A box is formed from a rectangular sheet of cardboard, which has a width of \( a \) units and a length of \( b \) units, by first cutting out squares of side length \( x \) units from each corner and then folding up to form an open-top container.
The maximum volume of the box occurs when \( x \) is equal to
- A. \( \frac{a - b + \sqrt{a^2 - ab + b^2}}{6} \)
- B. \( \frac{a + b + \sqrt{a^2 - ab + b^2}}{6} \)
- C. \( \frac{a - b - \sqrt{a^2 - ab + b^2}}{6} \)
- D. \( \frac{a + b - \sqrt{a^2 - ab + b^2}}{6} \)
- E. \( \frac{a + b - \sqrt{a^2 - 2ab + b^2}}{6} \)
A soccer player kicks a ball with an angle of elevation \( \theta^\circ \), where \( \theta \) is a normally distributed random variable with a mean of 42° and a standard deviation of 8°.
The horizontal distance that the ball travels before landing is given by the function \( d = 50 \sin(2\theta) \).
The probability that the ball travels more than 40 m horizontally before landing is closest to
- A. 0.969
- B. 0.937
- C. 0.226
- D. 0.149
- E. 0.027
End of Section A
Section B
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The diagram below shows part of the graph of \( y = f(x) \), where \( f(x) = \frac{x^2}{12} \).
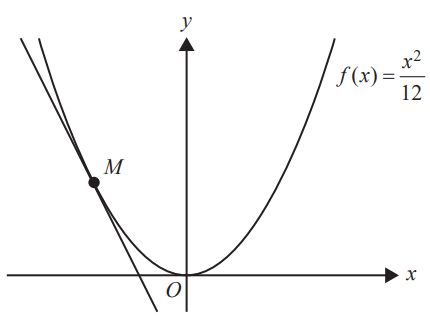
a. State the equation of the axis of symmetry of the graph of \( f \). 1 mark
b. State the derivative of \( f \) with respect to \( x \). 1 mark
The tangent to \( f \) at point M has gradient −2.
c. Find the equation of the tangent to \( f \) at point M. 2 marks
The diagram below shows part of the graph of \( y = f(x) \), the tangent to \( f \) at point M and the line perpendicular to the tangent at point M.
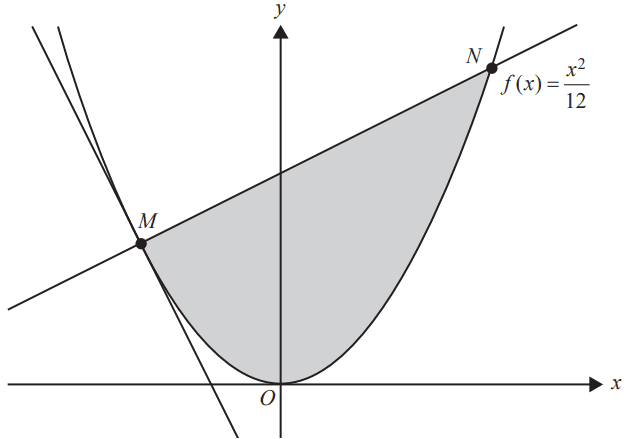
d. i. Find the equation of the line perpendicular to the tangent passing through point M. 1 mark
ii. The line perpendicular to the tangent at point M also cuts \( f \) at point N, as shown in the diagram above.
Find the area enclosed by this line and the curve \( y = f(x) \). 2 marks
e. Another parabola is defined by the rule \( g(x) = \frac{x^2}{4a} \), where \( a > 0 \).
A tangent to \( g \) and the line perpendicular to the tangent at \( x = -b \), where \( b > 0 \), are shown below.
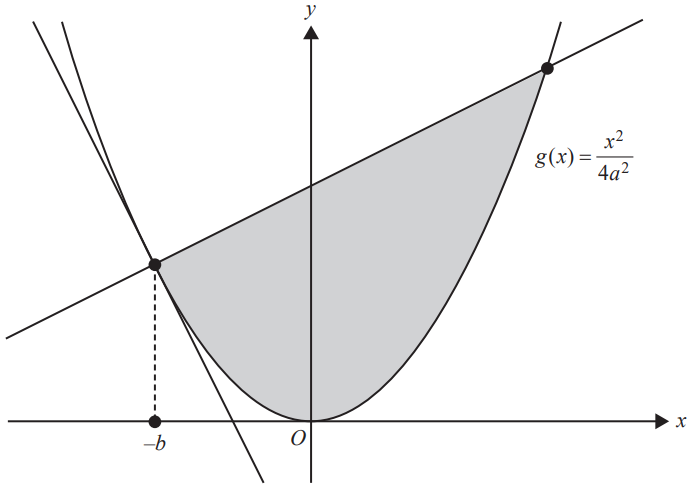
Find the value of \( b \), in terms of \( a \), such that the shaded area is a minimum. 4 marks
On a remote island, there are only two species of animals: foxes and rabbits. The foxes are the predators and the rabbits are their prey.
The populations of foxes and rabbits increase and decrease in a periodic pattern, with the period of both populations being the same, as shown in the graph below, for all \( t \geq 0 \), where time \( t \) is measured in weeks.
One point of minimum fox population, \( (20, 700) \), and one point of maximum fox population, \( (100, 2500) \), are also shown on the graph.
The graph has been drawn to scale.
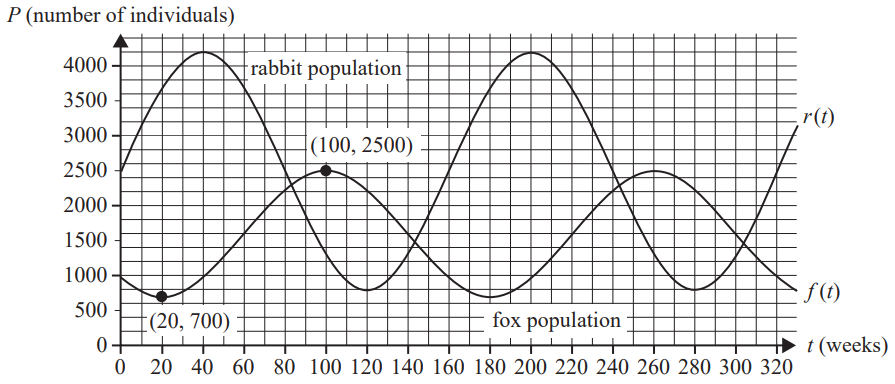
a. i. State the initial population of rabbits. 1 mark
ii. State the minimum and maximum population of rabbits. 1 mark
iii. State the number of weeks between maximum populations of rabbits. 1 mark
The population of foxes can be modelled by the rule \( f(t) = a \sin\big(b(t - 60)\big) + 1600 \).
b. Show that \( a = 900 \) and \( b = \frac{\pi}{80} \). 2 marks
c. Find the maximum combined population of foxes and rabbits. Give your answer correct to the nearest whole number. 1 mark
d. What is the number of weeks between the periods when the combined population of foxes and rabbits is a maximum? 1 mark
[The following question is no longer on the curriculum]
The population of foxes is better modelled by the transformation of \( y = \sin(t) \) under \( Q : \mathbb{R}^2 \rightarrow \mathbb{R}^2, \, Q \begin{pmatrix} t \\ y \end{pmatrix} = \begin{pmatrix} \frac{90}{\pi} & 0 \\ 0 & 900 \end{pmatrix} \begin{pmatrix} t \\ y \end{pmatrix} + \begin{pmatrix} 60 \\ 1600 \end{pmatrix} \).
e. Find the average population during the first 300 weeks for the combined population of foxes and rabbits, where the population of foxes is modelled by the transformation of \( y = \sin(t) \) under the transformation \( Q \). Give your answer correct to the nearest whole number. 4 marks
Over a longer period of time, it is found that the increase and decrease in the population of rabbits gets smaller and smaller.
The population of rabbits over a longer period of time can be modelled by the rule
\( s(t) = 1700 \cdot e^{-0.003t} \cdot \sin\left( \frac{\pi t}{80} \right) + 2500, \quad \text{for all } t \geq 0 \)
f. Find the average rate of change between the first two times when the population of rabbits is at a maximum. Give your answer correct to one decimal place. 2 marks
g. Find the time, where \( t > 40 \), in weeks, when the rate of change of the rabbit population is at its greatest positive value. Give your answer correct to the nearest whole number. 2 marks
h. Over time, the rabbit population approaches a particular value.
State this value. 1 mark
Mika is flipping a coin. The unbiased coin has a probability of \( \frac{1}{2} \) of landing on heads and \( \frac{1}{2} \) of landing on tails.
Let \( X \) be the binomial random variable representing the number of times that the coin lands on heads. Mika flips the coin five times.
a. i. Find \( \Pr(X = 5) \). 1 mark
ii. Find \( \Pr(X \geq 2) \). 1 mark
iii. Find \( \Pr(X \geq 2 \mid X < 5) \), correct to three decimal places. 2 marks
iv. Find the expected value and the standard deviation for \( X \). 2 marks
The height reached by each of Mika’s coin flips is given by a continuous random variable, \( H \), with the probability density function
\[ f(h) = \begin{cases} ah^2 + bh + c, & 1.5 \leq h \leq 3 \\ 0, & \text{otherwise} \end{cases} \]
where \( h \) is the vertical height reached by the coin flip, in metres, between the coin and the floor, and \( a, b, c \in \mathbb{R} \).
b. i. State the value of the definite integral \( \int_{1.5}^{3} f(h) \, dh \). 1 mark
ii. Given that \( \Pr(H \leq 2) = 0.35 \) and \( \Pr(H \geq 2.5) = 0.25 \), find the values of \( a \), \( b \), and \( c \). 3 marks
iii. The ceiling of Mika’s room is 3 m above the floor. The minimum distance between the coin and the ceiling is a continuous random variable, \( D \), with probability density function \( g \).
The function \( g \) is a transformation of the function \( f \) given by \( g(d) = f(rd + s) \), where \( d \) is the minimum distance between the coin and the ceiling, and \( r \) and \( s \) are real constants.
Find the values of \( r \) and \( s \). 1 mark
c. Mika’s sister Bella also has a coin. On each flip, Bella’s coin has a probability of \( p \) of landing on heads and \( (1 - p) \) of landing on tails, where \( p \) is a constant value between 0 and 1.
Bella flips her coin 25 times in order to estimate \( p \).
Let \( \hat{P} \) be the random variable representing the proportion of times that Bella’s coin lands on heads in her sample.
i. Is the random variable \( \hat{P} \) discrete or continuous? Justify your answer. 1 mark
ii. If \( \hat{p} = 0.4 \), find an approximate 95% confidence interval for \( p \), correct to three decimal places. 1 mark
iii. Bella knows that she can decrease the width of a 95% confidence interval by using a larger sample of coin flips.
If \( \hat{p} = 0.4 \), how many coin flips would be required to halve the width of the confidence interval found in part c.ii.? 1 mark
Consider the function \( f : \left( -\frac{1}{2}, \frac{1}{2} \right) \rightarrow \mathbb{R} \), \( f(x) = \log_e\left(x + \frac{1}{2}\right) - \log_e\left(\frac{1}{2} - x\right) \).
Part of the graph of \( y = f(x) \) is shown below.
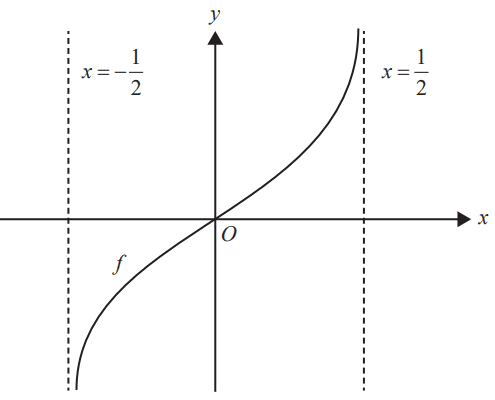
a. State the range of \( f(x) \). 1 mark
b. i. Find \( f'(0) \). 2 marks
ii. State the maximal domain over which \( f \) is strictly increasing. 1 mark
c. Show that \( f(x) + f(-x) = 0 \). 1 mark
d. Find the domain and the rule of \( f^{-1} \), the inverse of \( f \). 3 marks
Let \( h \) be the function \( h : \left( -\frac{1}{2}, \frac{1}{2} \right) \rightarrow \mathbb{R} \), \( h(x) = \frac{1}{k} \left( \log_e\left(x + \frac{1}{2}\right) - \log_e\left(\frac{1}{2} - x\right) \right) \), where \( k \in \mathbb{R} \) and \( k > 0 \).
The inverse function of \( h \) is defined by \( h^{-1} : \mathbb{R} \rightarrow \mathbb{R} \), \( h^{-1}(x) = \frac{e^{kx} - 1}{2(e^{kx} + 1)} \).
The area of the regions bound by the functions \( h \) and \( h^{-1} \) can be expressed as a function, \( A(k) \). The graph below shows the relevant area shaded.
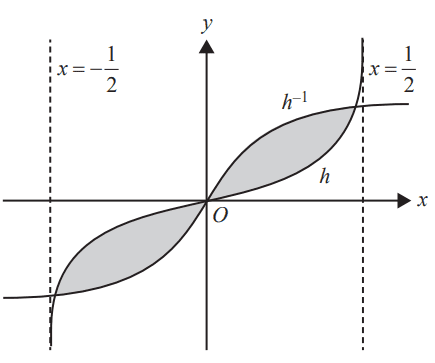
e. i. Determine the range of values of \( k \) such that \( A(k) > 0 \). 1 mark
Let \( g(x) = f(\sin(2x)) \), where the function \( f \) is differentiable.
The following table gives values for \( f(x) \) and \( f'(x) \):
| \( x \) | \( \frac{1}{2} \) | \( \frac{\sqrt{2}}{2} \) | \( \frac{\sqrt{3}}{2} \) |
|---|---|---|---|
| \( f(x) \) | \( -2 \) | \( 5 \) | \( 3 \) |
| \( f'(x) \) | \( 7 \) | \( 0 \) | \( \frac{1}{9} \) |
a. Find the value of \( g\left( \frac{\pi}{6} \right) \). 1 mark
The derivative of \( g \) with respect to \( x \) is given by \( g'(x) = 2 \cdot \cos(2x) \cdot f'(\sin(2x)) \).
b. Show that \( g'\left( \frac{\pi}{6} \right) = \frac{1}{9} \). 1 mark
c. Find the equation of the tangent to \( g \) at \( x = \frac{\pi}{6} \). 2 marks
d. Find the average value of the derivative function \( g'(x) \) between \( x = \frac{\pi}{8} \) and \( x = \frac{\pi}{6} \). 2 marks
e. Find four solutions to the equation \( g'(x) = 0 \) for the interval \( x \in [0, \pi] \). 3 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

