2023 VCAA Maths Methods Exam 2
This is the full VCE Maths Methods Exam with worked solutions. You can also try Mini-Tests, which are official VCAA exams split into short tests you can do anytime.
Number of marks: 80
Reading time: 15 minutes
Writing time: 2 hours
Section A – Multiple-choice questions
Instructions
• Answer all questions in pencil on your Multiple-Choice Answer Sheet.
• Choose the response that is correct for the question.
• A correct answer scores 1; an incorrect answer scores 0.
• Marks will not be deducted for incorrect answers.
• No marks will be given if more than one answer is completed for any question.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
The amplitude, \( A \), and the period, \( P \), of the function \( f(x) = -\frac{1}{2} \sin(3x + 2\pi) \) are
- A. \( A = -\frac{1}{2}, \quad P = \frac{\pi}{3} \)
- B. \( A = -\frac{1}{2}, \quad P = \frac{2\pi}{3} \)
- C. \( A = -\frac{1}{2}, \quad P = \frac{3\pi}{2} \)
- D. \( A = \frac{1}{2}, \quad P = \frac{\pi}{3} \)
- E. \( A = \frac{1}{2}, \quad P = \frac{2\pi}{3} \)
For the parabola with equation \( y = ax^2 + 2bx + c \), where \( a, b, c \in \mathbb{R} \), the equation of the axis of symmetry is
- A. \( x = -\frac{b}{a} \)
- B. \( x = -\frac{b}{2a} \)
- C. \( y = c \)
- D. \( x = \frac{b}{a} \)
- E. \( x = \frac{b}{2a} \)
Two functions, \( p \) and \( q \), are continuous over their domains, which are [−2, 3) and (−1, 5], respectively. The domain of the sum function \( p + q \) is
- A. [−2, 5]
- B. [−2, −1) ∪ (3, 5]
- C. [−2, −1) ∪ (−1, 3) ∪ (3, 5]
- D. [−1, 3]
- E. (−1, 3)
Consider the system of simultaneous linear equations below containing the parameter \( k \):
\( kx + 5y = k + 5 \)
\( 4x + (k + 1)y = 0 \)
The value(s) of \( k \) for which the system of equations has infinite solutions are
- A. \( k \in \{-5, 4\} \)
- B. \( k \in \{-5\} \)
- C. \( k \in \{4\} \)
- D. \( k \in \mathbb{R} \setminus \{-5, 4\} \)
- E. \( k \in \mathbb{R} \setminus \{-5\} \)
Which one of the following functions has a horizontal tangent at (0, 0)?
- A. \( y = x^{-1/3} \)
- B. \( y = x^{1/3} \)
- C. \( y = x^{2/3} \)
- D. \( y = x^{4/3} \)
- E. \( y = x^{3/4} \)
Suppose that \( \int_3^{10} f(x)\, dx = C \) and \( \int_7^{10} f(x)\, dx = D \). The value of \( \int_3^7 f(x)\, dx \) is
- A. \( C + D \)
- B. \( C + D - 3 \)
- C. \( C - D \)
- D. \( D - C \)
- E. \( CD - 3 \)
Let \( f(x) = \log_e x \), where \( x > 0 \) and \( g(x) = \sqrt{1 - x} \), where \( x < 1 \).
The domain of the derivative of \( (f \circ g)(x) \) is
- A. \( x \in \mathbb{R} \)
- B. \( x \in (-\infty, 1] \)
- C. \( x \in (-\infty, 1) \)
- D. \( x \in (0, \infty) \)
- E. \( x \in (0, 1) \)
A box contains \( n \) green balls and \( m \) red balls. A ball is selected at random, and its colour is noted. The ball is then replaced in the box. In 8 such selections, where \( n \ne m \), what is the probability that a green ball is selected at least once?
- A. \( 8 \left( \frac{n}{n + m} \right) \left( \frac{m}{n + m} \right)^7 \)
- B. \( 1 - \left( \frac{n}{n + m} \right)^8 \)
- C. \( 1 - \left( \frac{m}{n + m} \right)^8 \)
- D. \( 1 - \left( \frac{n}{n + m} \right) \left( \frac{m}{n + m} \right)^7 \)
- E. \( 1 - 8 \left( \frac{n}{n + m} \right) \left( \frac{m}{n + m} \right)^7 \)
\[ f(x) = \begin{cases} \tan\left(\frac{x}{2}\right) & 4 \leq x < 2\pi \\ \sin(ax) & 2\pi \leq x \leq 8 \end{cases} \]
The value of \( a \) for which \( f \) is continuous and smooth at \( x = 2\pi \) is- A. −2
- B. \( -\sqrt{2} \)
- C. \( -\frac{1}{2} \)
- D. \( \frac{1}{2} \)
- E. 2
A continuous random variable \( X \) has the following probability density function:
\[ g(x) = \begin{cases} \frac{x - 1}{20} & 1 \leq x < 6 \\ \frac{9 - x}{12} & 6 \leq x \leq 9 \\ 0 & \text{elsewhere} \end{cases} \]
The value of \( k \) such that \( \Pr(X < k) = 0.35 \) is
- A. \( \sqrt{14} - 1 \)
- B. \( \sqrt{14} + 1 \)
- C. \( \sqrt{15} - 1 \)
- D. \( \sqrt{15} + 1 \)
- E. \( 1 - \sqrt{15} \)
Two functions, \( f \) and \( g \), are continuous and differentiable for all \( x \in \mathbb{R} \). It is given that
\( f(-2) = -7, \quad g(-2) = 8, \quad f'(-2) = 3, \quad g'(-2) = 2 \)
The gradient of the graph \( y = f(x) \times g(x) \) at \( x = -2 \) is
- A. −10
- B. −6
- C. 0
- D. 6
- E. 10
The probability mass function for the discrete random variable \( X \) is shown below:
| X | −1 | 0 | 1 | 2 |
|---|---|---|---|---|
| Pr(\(X = x\)) | \(k^2\) | \(3k\) | \(k\) | \(-k^2 - 4k + 1\) |
The maximum possible value for the mean of \( X \) is:
- A. 0
- B. \( \frac{1}{3} \)
- C. \( \frac{2}{3} \)
- D. 1
- E. 2
The following algorithm applies Newton’s method using a For loop with 3 iterations...
\[ \begin{array}{l} \textbf{Inputs:} \quad f(x), \text{ a function of } x \\ \quad\quad\quad\quad df(x), \text{ the derivative of } f(x) \\ \quad\quad\quad\quad x_0, \text{ an initial estimate} \\ \\ \textbf{Define } \texttt{newton}(f(x), df(x), x_0) \\ \quad \textbf{For } i \text{ from } 1 \text{ to } 3 \\ \quad\quad \textbf{If } df(x_0) = 0 \textbf{ Then} \\ \quad\quad\quad \textbf{Return } \text{``Error: Division by zero''} \\ \quad\quad \textbf{Else} \\ \quad\quad\quad x_0 \leftarrow x_0 - f(x_0) \div df(x_0) \\ \quad \textbf{EndFor} \\ \quad \textbf{Return } x_0 \end{array} \]The return value of the function newton(x³ + 3x − 3, 3x² + 3, 1) is closest to
- A. 0.83333
- B. 0.81785
- C. 0.81773
- D. 1
- E. 3
A polynomial has the equation \( y = x(3x - 1)(x + 3)(x + 1) \).
The number of tangents to this curve that pass through the positive x-intercept is
- A. 0
- B. 1
- C. 2
- D. 3
- E. 4
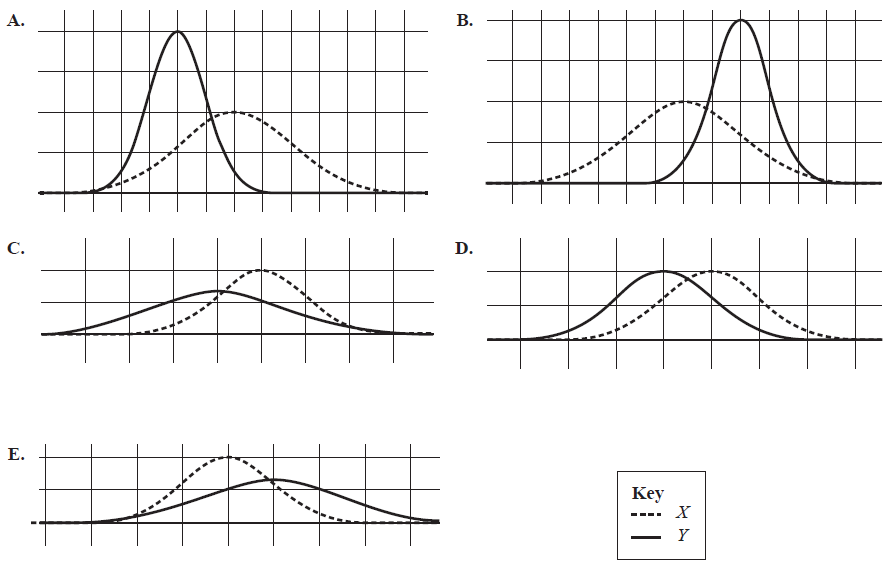
Let \( X \) be a normal random variable with mean 100 and standard deviation 20.
Let \( Y \) be a normal random variable with mean 80 and standard deviation 10.
Which of the diagrams below best represents the probability density functions for \( X \) and \( Y \), plotted on the same set of axes?
Let \( f(x) = e^{x - 1} \).
Given that the product function \( f(x) \times g(x) = e^{(x - 1)^2} \), the rule for the function \( g \) is:
- A. \( g(x) = e^{x - 1} \)
- B. \( g(x) = e^{(x - 2)(x - 1)} \)
- C. \( g(x) = e^{(x + 2)(x - 1)} \)
- D. \( g(x) = e^{x(x - 2)} \)
- E. \( g(x) = e^{x(x - 3)} \)
A cylinder of height \( h \) and radius \( r \) is formed from a rectangular metal sheet of length \( x \) and width \( y \), by cutting
along the dashed lines shown below.
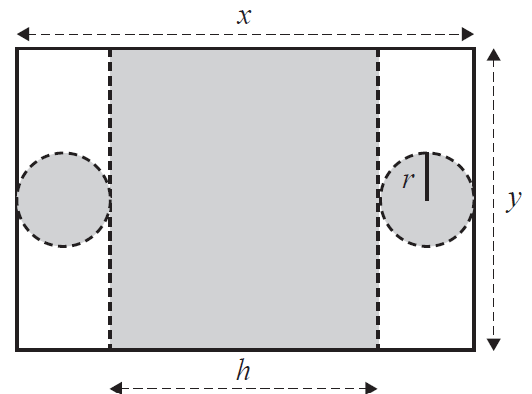
The volume of the cylinder in terms of \( x \) and \( y \) is
- A. \( \pi x^2 y \)
- B. \( \frac{\pi x y^2 - 2 y^3}{4\pi^2} \)
- C. \( \frac{2 y^3 - \pi x y^2}{4\pi^2} \)
- D. \( \frac{\pi x y - 2 y^2}{2\pi} \)
- E. \( \frac{2 y^2 - \pi x y}{2\pi} \)
Consider the function \( f : [-a\pi, a\pi] \to \mathbb{R} \), \( f(x) = \sin(ax) \), where \( a \) is a positive integer.
The number of local minima in the graph of \( y = f(x) \) is always equal to
- A. 2
- B. 4
- C. \( a \)
- D. \( 2a \)
- E. \( a^2 \)
Find all values of \( k \), such that the equation
\( x^2 + (4k + 3)x + 4k^2- \frac{9}{4} = 0 \)
has two real solutions for \( x \), one positive and one negative.
- A. \( k > -\frac{3}{4} \)
- B. \( k \geq -\frac{3}{4} \)
- C. \( k > \frac{3}{4} \)
- D. \( -\frac{3}{4} < k < \frac{3}{4} \)
- E. \( k < -\frac{3}{4} \text{ or } k > \frac{3}{4} \)
Let \( f(x) = \log_e\left(x + \frac{1}{\sqrt{2}}\right) \).
Let \( g(x) = \sin(x) \) where \( x \in (-\infty, 5) \).
The largest interval of \( x \) values for which \( (f \circ g)(x) \) and \( (g \circ f)(x) \) both exist is
- A. \( \left( -\frac{1}{\sqrt{2}}, \frac{5\pi}{4} \right) \)
- B. \( \left[ -\frac{1}{\sqrt{2}}, \frac{5\pi}{4} \right) \)
- C. \( \left( -\frac{\pi}{4}, \frac{5\pi}{4} \right) \)
- D. \( \left[ -\frac{\pi}{4}, \frac{5\pi}{4} \right) \)
- E. \( \left[ -\frac{\pi}{4}, -\frac{1}{\sqrt{2}} \right] \)
End of Section A
Section B
Instructions
• Answer all questions in the spaces provided.
• Write your responses in English.
• In questions where a numerical answer is required, an exact value must be given unless otherwise specified.
• In questions where more than one mark is available, appropriate working must be shown.
• Unless otherwise indicated, the diagrams in this book are not drawn to scale.
Let \( f : \mathbb{R} \rightarrow \mathbb{R} \), \( f(x) = x(x - 2)(x + 1) \). Part of the graph of \( f \) is shown below.
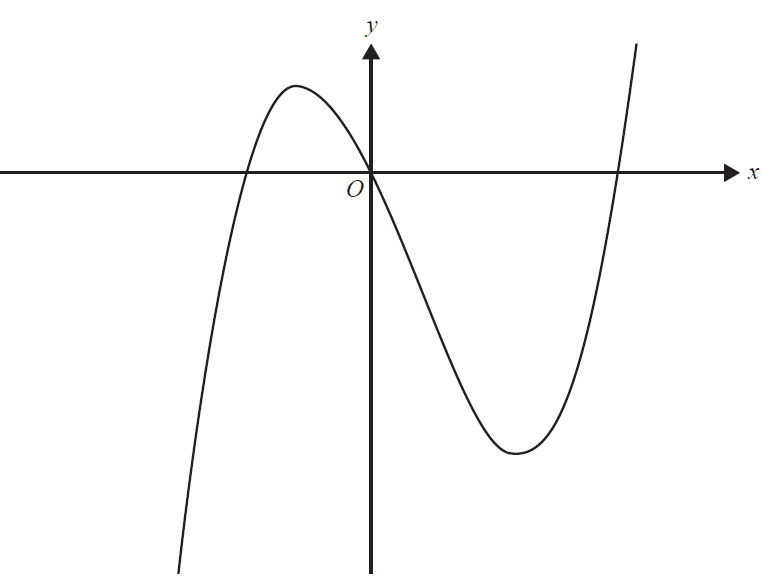
a. State the coordinates of all axial intercepts of \( f \). 1 mark
b. Find the coordinates of the stationary points of \( f \). 2 marks
c. i. Let \( g : \mathbb{R} \rightarrow \mathbb{R} \), \( g(x) = x - 2 \). Find the values of \( x \) for which \( f(x) = g(x) \). 1 mark
ii. Write down an expression using definite integrals that gives the area of the regions bound by \( f \) and \( g \). 2 marks
iii. Hence, find the total area of the regions bound by \( f \) and \( g \), correct to two decimal places. 1 mark
d. Let \( h : \mathbb{R} \rightarrow \mathbb{R} \), \( h(x) = (x - a)(x - b)^2 \), where \( h(x) = f(x) + k \) and \( a, b, k \in \mathbb{R} \). Find the possible values of \( a \) and \( b \). 4 marks
The following diagram represents an observation wheel, with its centre at point P. Passengers are seated in pods, which are carried around as the wheel turns. The wheel moves anticlockwise with constant speed and completes one full rotation every 30 minutes. When a pod is at the lowest point of the wheel (point A), it is 15 metres above the ground. The wheel has a radius of 60 metres.
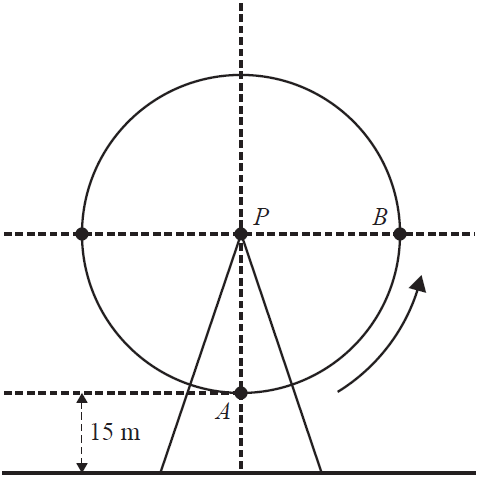
Consider the function \( h(t) = -60 \cos(bt) + c \) for some \( b, c \in \mathbb{R} \), which models the height above the ground of a pod originally situated at point A, after time \( t \) minutes.
a. Show that \( b = \frac{\pi}{15} \) and \( c = 75 \). 2 marks
b. Find the average height of a pod on the wheel as it travels from point A to point B. Give your answer in metres, correct to two decimal places. 2 marks
c. Find the average rate of change, in metres per minute, of the height of a pod on the wheel as it travels from point A to point B. 1 mark
After 15 minutes, the wheel stops moving and remains stationary for 5 minutes. After this, it continues moving at double its previous speed for another 7.5 minutes. The height above the ground of a pod that was initially at point A, after \( t \) minutes, can be modelled by the piecewise function \( w \):
\[ w(t) = \begin{cases} h(t) & 0 \leq t < 15 \\ k & 15 \leq t < 20 \\ h(mt + n) & 20 \leq t \leq 27.5 \end{cases} \] where \( k \geq 0 \), \( m \geq 0 \) and \( n \in \mathbb{R} \).
d. i. State the values of \( k \) and \( m \). 1 mark
ii. Find all possible values of \( n \). 2 marks
iii. Sketch the graph of the piecewise function \( w \) on the axes below, showing the coordinates of the endpoints. 3 marks
Consider the function \( g : \mathbb{R} \rightarrow \mathbb{R} \), \( g(x) = 2^x + 5 \).
a. State the value of \( \lim_{x \to -\infty} g(x) \). 1 mark
b. The derivative, \( g'(x) \), can be expressed in the form \( g'(x) = k \times 2^x \). Find the real number \( k \). 1 mark
c. i. Let \( a \) be a real number. Find, in terms of \( a \), the equation of the tangent to \( g \) at the point \( (a, g(a)) \). 1 mark
ii. Hence, or otherwise, find the equation of the tangent to \( g \) that passes through the origin, correct to three decimal places. 2 marks
Let \( h : \mathbb{R} \rightarrow \mathbb{R} \), \( h(x) = 2^x - x^2 \).
d. Find the coordinates of the point of inflection for \( h \), correct to two decimal places. 1 mark
e. Find the largest interval of \( x \) values for which \( h \) is strictly decreasing. Give your answer correct to two decimal places. 1 mark
f. Apply Newton’s method, with an initial estimate of \( x_0 = 0 \), to find an approximate x-intercept of \( h \). Write the estimates \( x_1 \), \( x_2 \) and \( x_3 \) in the table below, correct to three decimal places. 2 marks
| \( x_0 \) | 0 |
| \( x_1 \) | |
| \( x_2 \) | |
| \( x_3 \) |
g. For the function \( h \), explain why a solution to the equation \( \log_e(2) \times 2^x - 2x = 0 \) should not be used as an initial estimate \( x_0 \) in Newton’s method. 1 mark
h. There is a positive real number \( n \) for which the function \( f(x) = n^x - x^n \) has a local minimum on the x-axis. Find this value of \( n \). 2 marks
A manufacturer produces tennis balls. The diameter of the tennis balls is a normally distributed random variable \( D \), which has a mean of 6.7 cm and a standard deviation of 0.1 cm.
a. Find \( \Pr(D > 6.8) \), correct to four decimal places. 1 mark
b. Find the minimum diameter of a tennis ball that is larger than 90% of all tennis balls produced. Give your answer in centimetres, correct to two decimal places. 1 mark
Tennis balls are packed and sold in cylindrical containers. A tennis ball can fit through the opening at the top of the container if its diameter is smaller than 6.95 cm.
c. Find the probability that a randomly selected tennis ball can fit through the opening at the top of the container. Give your answer correct to four decimal places. 1 mark
d. In a random selection of 4 tennis balls, find the probability that at least 3 balls can fit through the opening at the top of the container. Give your answer correct to four decimal places. 2 marks
A tennis ball is classed as grade A if its diameter is between 6.54 cm and 6.86 cm, otherwise it is classed as grade B.
e. Given that a tennis ball can fit through the opening at the top of the container, find the probability that it is classed as grade A. Give your answer correct to four decimal places. 2 marks
f. The manufacturer would like to improve processes to ensure that more than 99% of all tennis balls produced are classed as grade A. Assuming that the mean diameter of the tennis balls remains the same, find the required standard deviation of the diameter, in centimetres, correct to two decimal places. 2 marks
g. An inspector takes a random sample of 32 tennis balls from the manufacturer and determines a confidence interval for the population proportion of grade A balls produced. The confidence interval is (0.7382, 0.9493), correct to 4 decimal places.
Find the level of confidence that the population proportion of grade A balls is within the interval, as a percentage correct to the nearest integer. 2 marks
A tennis coach uses both grade A and grade B balls. The serving speed, in metres per second, of a grade A ball is a continuous random variable, \( V \), with the probability density function
\[ f(v) = \begin{cases} \frac{1}{6\pi} \sin\left( \sqrt{\frac{v - 30}{3}} \right), & 30 \leq v \leq 3\pi^2 + 30 \\ 0, & \text{elsewhere} \end{cases} \]
h. Find the probability that the serving speed of a grade A ball exceeds 50 metres per second. Give your answer correct to four decimal places. 1 mark
i. Find the exact mean serving speed for grade A balls, in metres per second. 1 mark
The serving speed of a grade B ball is given by a continuous random variable, \( W \), with the probability density function \( g(w) \).
A transformation maps the graph of \( f \) to the graph of \( g \), where
\[ g(w) = af\left(\frac{w}{b}\right) \]
j. If the mean serving speed for a grade B ball is \( 2\pi^2 + 8 \) metres per second, find the values of \( a \) and \( b \). 2 marks
Let \( f : \mathbb{R} \rightarrow \mathbb{R} \), \( f(x) = e^x + e^{-x} \) and \( g : \mathbb{R} \rightarrow \mathbb{R} \), \( g(x) = \frac{1}{2} f(2-x) \).
a. Complete a possible sequence of transformations to map \( f \) to \( g \). 2 marks
- • Dilation of factor \( \frac{1}{2} \) from the x-axis.
- •
- •
Two functions \( g_1 \) and \( g_2 \) are created, both with the same rule as \( g \) but with distinct domains, such that \( g_1 \) is strictly increasing and \( g_2 \) is strictly decreasing.
b. Give the domain and range for the inverse of \( g_1 \). 2 marks
Shown below is the graph of \( g \), the inverses of \( g_1 \) and \( g_2 \), and the line \( y = x \).
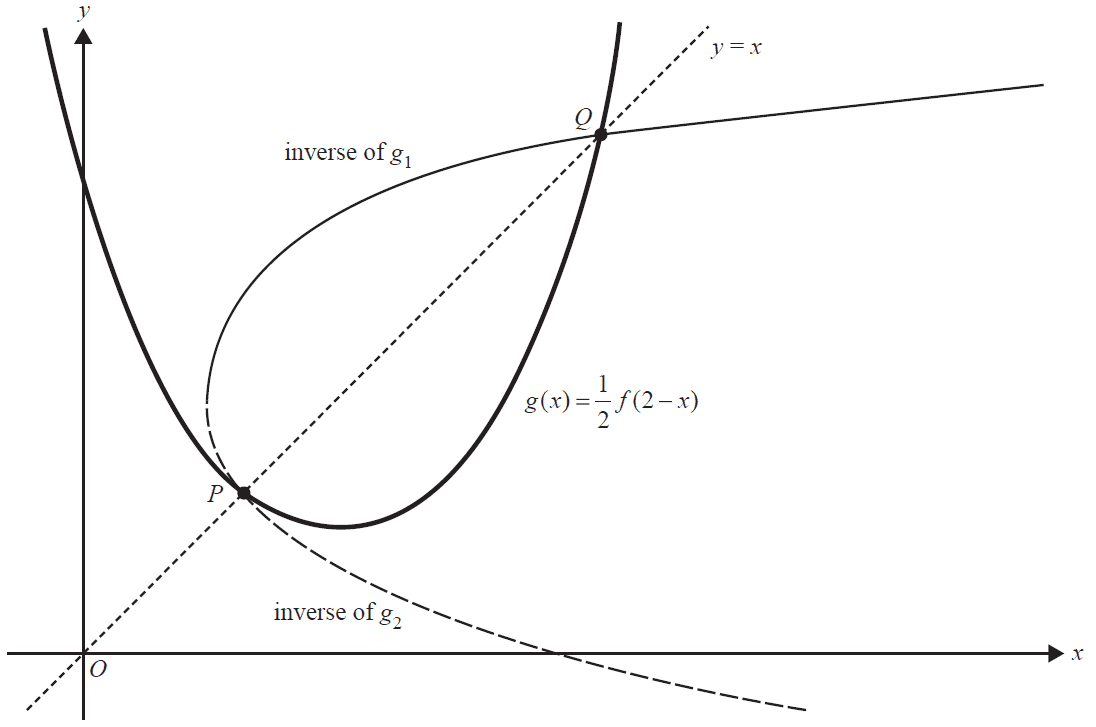
The intersection points between the graphs of \( y = x \), \( y = g(x) \) and the inverses of \( g_1 \) and \( g_2 \), are labelled P and Q.
c. i. Find the coordinates of \( P \) and \( Q \), correct to two decimal places. 1 mark
ii. Find the area of the region bound by the graphs of \( g \), the inverse of \( g_1 \) and the inverse of \( g_2 \). Give your answer correct to two decimal places. 2 marks
Let \( h : \mathbb{R} \rightarrow \mathbb{R} \), \( h(x) = \frac{1}{k} f(k-x) \), where \( k \in (0, \infty) \).
d. The turning point of \( h \) always lies on the graph of the function \( y = 2x^n \), where \( n \) is an integer. Find the value of \( n \). 1 mark
Let \( h_1 : [k, \infty) \rightarrow \mathbb{R} \), \( h_1(x) = h(x) \). The rule for the inverse of \( h_1 \) is \( y = \log_e\left( \frac{k}{2}x + \frac{1}{2} \sqrt{k^2 x^2 - 4} \right) + k \).
e. What is the smallest value of \( k \) such that \( h \) will intersect with the inverse of \( h_1 \)? Give your answer correct to two decimal places. 1 mark
It is possible for the graphs of \( h \) and the inverse of \( h_1 \) to intersect twice. This occurs when \( k = 5 \).
f. Find the area of the region bound by the graphs of \( h \) and the inverse of \( h_1 \), when \( k = 5 \). Give your answer correct to two decimal places. 2 marks
End of examination questions
VCE is a registered trademark of the VCAA. The VCAA does not endorse or make any warranties regarding this study resource. Past VCE exams and related content can be accessed directly at www.vcaa.vic.edu.au

