Question 1 (6 marks) [2019 Section 1 Q1]

Consider the derivative function \(f'(x) = xe^{x^2}\).

(a) Determine \(f''(1)\). (2 marks)

(b) Explain the meaning of your answer to part (a). (1 mark)

(c) Determine the expression for \(y=f(x)\), given that it intersects the y-axis at the point (0,2). (3 marks)

Question 2 (6 marks) [2019 Section 1 Q2]

The values of the functions \(g(x)\) and \(h(x)\), and their derivatives \(g'(x)\) and \(h'(x)\) are provided in the table below for \(x=1\), \(x=2\) and \(x=3\).

	\(x=1\)	\(x=2\)	\(x=3\)
\(g(x)\)	3	5	-3
\(h(x)\)	2	-2	6
\(g'(x)\)	-4	1	4
\(h'(x)\)	0	-6	-5

(a) Evaluate the derivative of \(\frac{g(x)}{h(x)}\) at \(x=3\). (2 marks)

(b) Evaluate the derivative of \(h(g(x))\) at \(x=1\). (2 marks)

(c) If \(h''(1) = -1\), describe with justification, what the graph of \(h(x)\) looks like at this point. (2 marks)

Question 3 (7 marks) [2019 Section 1 Q3]

Waiting times for patients at a hospital emergency department can be up to four hours. The associated probability density function is shown below.

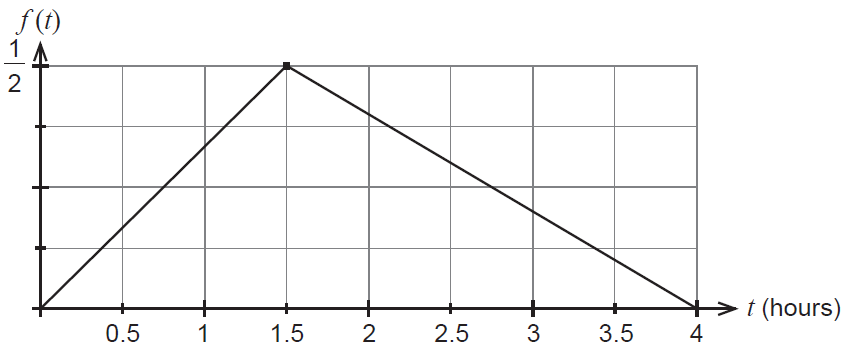
(a) What is the probability a patient will wait less than one hour? (3 marks)

(b) What is the probability a patient will wait between one hour and three hours? (4 marks)

Question 4 (6 marks) [2019 Section 1 Q4]

Consider the graph of \(y=\ln(x)\) shown below.

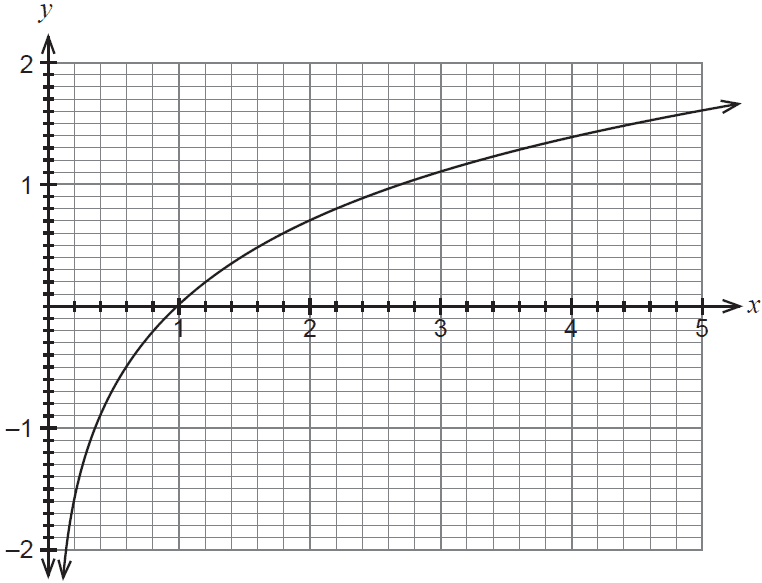
(a) Use the graph to estimate the value of \(p\) in each of the following.

(i) \(1.4 = \ln(p)\) (1 mark)

(ii) \(e^{p+1}-3=0\) (2 marks)

(b) On the axes below, sketch the graph of \(y = \ln(x-2)+1\). (3 marks)

Question 5 (8 marks) [2019 Section 1 Q5]

(a) Determine the area bound by the graph of \(f(x)=e^x\) and the x-axis between \(x=0\) and \(x=\ln 2\). (3 marks)

(b) Hence, determine the area bound by the graph of \(f(x)=e^x\), the line \(y=2\) and the y-axis. (2 marks)

(c) Determine the area bound by the graph of \(f(x)=e^x\), the line \(y=a\) and the y-axis, where \(a\) is a positive constant. (3 marks)

Question 6 (10 marks) [2019 Section 1 Q6]

The error \(X\) in digitising a communication signal has a uniform distribution with probability density function given by

\[ f(x) = \begin{cases} 1, & -0.5 < x < 0.5, \\ 0, & \text{otherwise.} \end{cases} \]

(a) Sketch the graph of \(f(x)\). (2 marks)

(b) What is the probability that the error is at least 0.35? (1 mark)

(c) If the error is negative, what is the probability that it is less than -0.35? (2 marks)

(d) An engineer is more interested in the square of the error. What is the probability that the square of the error is less than 0.09? (2 marks)

(e) Calculate the variance of the error. (3 marks)

Question 7 (9 marks) [2019 Section 1 Q7]

A company's profit, in millions of dollars, over a five-year period can be modelled by the function: \(P(t) = 2t\sin(3t)\) \(0 \le t \le 5\) where \(t\) is measured in years.

The graph of \(P(t)\) is shown below.

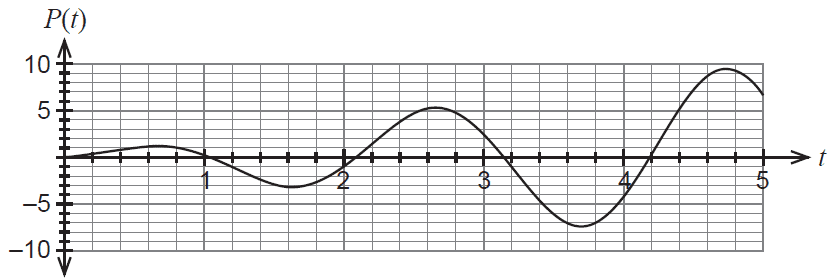
(a) Differentiate \(P(t)\) to determine the marginal profit function, \(P'(t)\). (2 marks)

(b) Calculate the rate of change of the marginal profit function when \(t = \frac{\pi}{18}\) years. (4 marks)

(c) Use the increments formula at \(t = \frac{7\pi}{6}\) to estimate the change in profit for a one month change in time. (3 marks)

Question 8 (7 marks) [2019 Section 2 Q8]

Big Foods is a large supermarket company. The manager of Big Foods wants to estimate the proportion of households that do the majority of their grocery shopping in their stores.

A junior staff member at Big Foods conducted a survey of 250 randomly-selected households and found that 56 did the majority of their grocery shopping at a Big Foods store.

(a)

(i) Calculate the sample proportion of households who did the majority of their grocery shopping at Big Foods. (1 mark)

(ii) Determine the 95% confidence interval for the proportion of households who do the majority of their grocery shopping at Big Foods. Give your answer to four decimal places. (3 marks)

(iii) What is the margin of error of the 95% confidence interval? Give your answer to four decimal places. (1 mark)

An independent research company conducted a large-scale survey of household supermarket preferences and estimated that the true proportion of households that conduct most of their grocery shopping at Big Foods was 0.17 (assume that this is indeed the true proportion).

(b) With reference to your answer to part (a)(ii), does this result suggest that the junior staff member at Big Foods made a mistake? (2 marks)

Question 9 (8 marks) [2019 Section 2 Q9]

It takes an elevator 16 seconds to ascend from the ground floor of a building to the sixth floor. The velocity of the elevator during its ascent is given by

\[ v(t) = \frac{9\pi}{16} \sin\left(\frac{\pi t}{16}\right) \text{ m/s.} \]

The velocity, \(v\), is measured in metres per second, while the time, \(t\), is measured in seconds.

(a) Determine the acceleration of the elevator during its ascent and provide a sketch of the acceleration function for \(0 \le t \le 16\). (2 marks)

(b) With reference to your answer from part (a), explain what is happening to the velocity of the elevator in the interval \(0 < t < 8\) and in the interval \(8 < t < 16\). (3 marks)

(c) Suppose that the ground floor has displacement \(x = 0\) m. Determine the displacement function of the elevator and hence determine the height above the ground floor of the sixth floor. (3 marks)

Question 10 (7 marks) [2019 Section 2 Q10]

A group of researchers conducted a study into the number of siblings of adult Australian citizens. They surveyed a total of 200 participants and recorded the number of siblings, \(X\), of each participant.

A few days later the lead researcher discovered that the survey data had been misplaced. Fortunately, one of the research assistants had been doing some rough calculations on a whiteboard and the lead researcher was able to recover the following information about the probability distribution for \(X\) and the mean \(\mu\).

\(x\)	0	1	2	3
\(P(X=x)\)	0.2	\(a\)	\(b\)	0.1

\(\mu = 1.3\)

The letters \(a\) and \(b\) have been used to denote unknown probabilities.

(a)

(i) Write two independent equations for \(a\) and \(b\). (2 marks)

(ii) Hence solve for the unknown probabilities. (2 marks)

Later that day the research assistant found the complete probability distribution in their records and discovered that they had made an error in their original calculation of the mean. The correct probability distribution is given in the table below.

\(x\)	0	1	2	3
\(P(X=x)\)	0.2	0.3	0.4	0.1

(b)

(i) Given that there were 200 participants in the study, complete the table below to show the number of participants \(N\) with 0, 1, 2 and 3 siblings. (1 mark)

\(x\)	0	1	2	3
\(P(X=x)\)	0.2	0.3	0.4	0.1
\(N\)	40

(ii) Determine the correct mean and standard deviation of the number of siblings \(X\). (2 marks)

Question 11 (8 marks) [2019 Section 2 Q11]

A pizza company runs a marketing campaign based on the delivery times of its pizzas. The company claims that it will deliver a pizza in a radius of 5 km within 30 minutes of ordering or it is free. The manager estimates that the actual time, \(T\), from order to delivery is normally distributed with mean 25 minutes and standard deviation 2 minutes.

(a) What is the probability that a pizza is delivered free? (1 mark)

(b) On a busy Saturday evening, a total of 50 pizzas are ordered. What is the probability that more than three are delivered free? (2 marks)

The company wants to reduce the proportion of pizzas that are delivered free to 0.1%.

(c) The manager suggests this can be achieved by increasing the advertised delivery time. What should the advertised delivery time be? (2 marks)

After some additional training the company was able to maintain the advertised delivery time as 30 minutes but reduce the proportion of pizzas delivered free to 0.1%.

(d) Assuming that the original mean of 25 minutes is maintained, what is the new standard deviation of delivery times? (3 marks)

Question 12 (6 marks) [2019 Section 2 Q12]

Part of Josie's workout at her gym involves a 10 minute run on a treadmill. The treadmill's program makes her run at a constant 12.3 km/h for the first 2 minutes and then her speed, \(s(t)\), is determined by the equation below, where \(t\) is the time in minutes after she began running.

\[ s(t) = 10 - \frac{\ln(t-1.99)}{t} \text{ km/h} \]

(a) Sketch the graph of her speed during this run versus time on the axes below. (3 marks)

(b) At what time(s) is Josie's speed 10 km/h? (1 mark)

(c) At what time(s) during her run is Josie's acceleration zero? (2 marks)

Question 13 (8 marks) [2019 Section 2 Q13]

The proportion of working adults who miss breakfast on week days is estimated to be 40%. A study takes a random sample of 400 working adults.

(a) For this sample:

(i) What is the (approximate) distribution of the sample proportion of workers who miss breakfast? (2 marks)

(ii) What is the probability that the sample proportion of workers who miss breakfast is greater than 44%? (2 marks)

Tom takes a random sample of 400 adults. He obtained his sample by selecting the first 400 workers he met in a busy mall in Perth city during lunch time.

(b) Discuss briefly two possible sources of bias in Tom's sample. (2 marks)

Amir suggests that a better sampling scheme is to obtain a random sample of 400 voters and contact them by telephone.

(c)

(i) Outline one source of bias in Amir's sampling scheme. (1 mark)

(ii) Which of Tom's or Amir's sampling scheme is better? Provide a reason for your choice. (1 mark)

Question 14 (7 marks) [2019 Section 2 Q14]

(a) What is the minimum sample size required to estimate a population proportion to within 0.01 with 95% confidence. (3 marks)

(b) Identify two factors that affect the width of a confidence interval for a population proportion and describe the effect of each. (4 marks)

Question 15 (14 marks) [2019 Section 2 Q15]

A wall in a new Western Australian hotel is to feature a rolling, wave-shaped window. Engineers have modelled the top edge of the wave shape by joining together two functions,

\(h_1(x) = 4 - 4(x-1)^2\), \(0 \le x \le 1\) and

\(h_2(x) = a(\cos(x-1)+1)\), \(1 < x \le d\) \(a,d\) constants.

The functions give the height, \(h\), above ground level of the top edge of the window measured in metres. The origin is defined as the leftmost point of the window which is at ground level and \(x\) is the horizontal distance to the right of the origin measured in metres. The graph of the two functions is shown below.

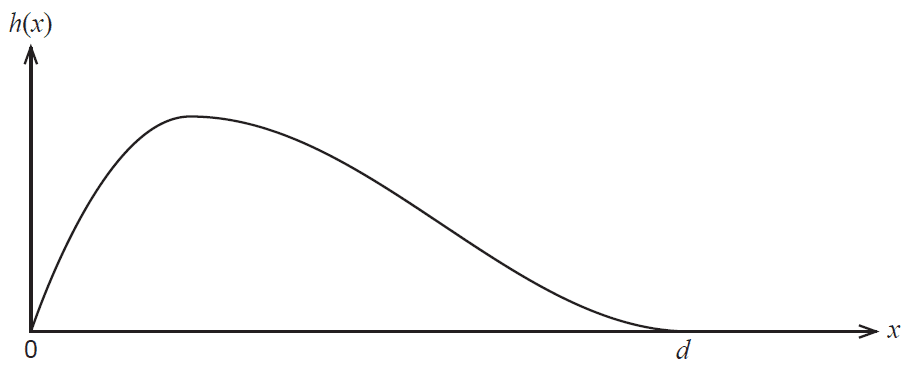
(a) Determine the value of the constant \(a\) in the function \(h_2(x) = a(\cos(x-1)+1)\). (3 marks)

(b) Determine the length of the bottom edge of the window. (2 marks)

(c) Determine the volume of glass required for the window if it has a uniform thickness of 3 cm. (5 marks)

The top edge of the wall, shown as the line AB below, is to just touch the window at the point C shown below. Point A is 1.39 m above the point B.

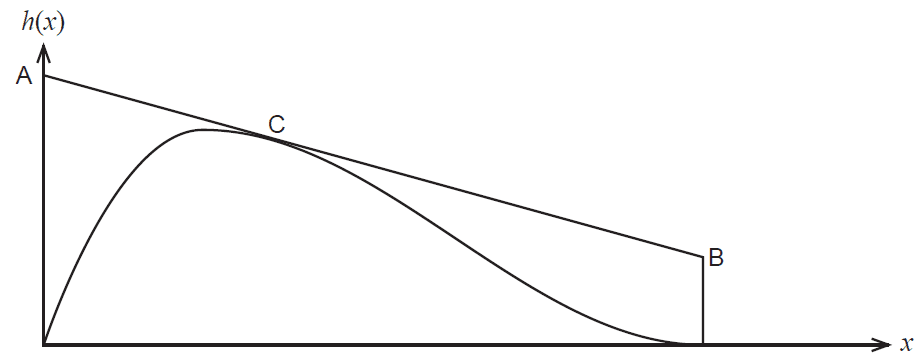
(d) How high is point C above the ground? (4 marks)

Question 16 (10 marks) [2019 Section 2 Q16]

A cylindrical glass vase is filled with 20 spherical Christmas decorations as shown below (not all the decorations are visible). All the decorations have a diameter of one-third the internal diameter of the vase and they are completely contained within the vase. For design purposes the sum of the internal diameter of the base of the vase and the vase's internal height is to be 42 cm.

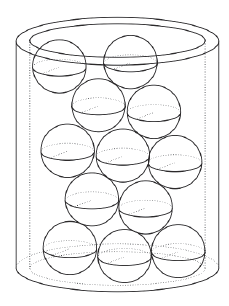
(a) Show that the volume of unused space in the vase, \(V\), can be expressed as a function of the internal radius of the vase, \(r\), and is given below as

\[ V(r) = 2\pi\left(21r^2 - \frac{121}{81}r^3\right) \] (3 marks)

(b) Use calculus to determine the dimensions of the vase that will maximise the unused space in it. Give your answers rounded to the nearest millimetre. (4 marks)

(c) Can more than 20 of the spherical decorations fit inside the vase in part (b)? Use calculations to verify your answer. (3 marks)

Question 17 (15 marks) [2019 Section 2 Q17]

A microbiologist is studying the effect of temperature on the growth of a certain type of bacteria under controlled laboratory conditions. A population of bacteria is incubated at a temperature of 30 °C and the size of the population measured at hourly intervals for six hours. The logarithm of the population size appears to lie on a straight line when plotted against time (measured in hours) and the line of best fit shown on the axes below.

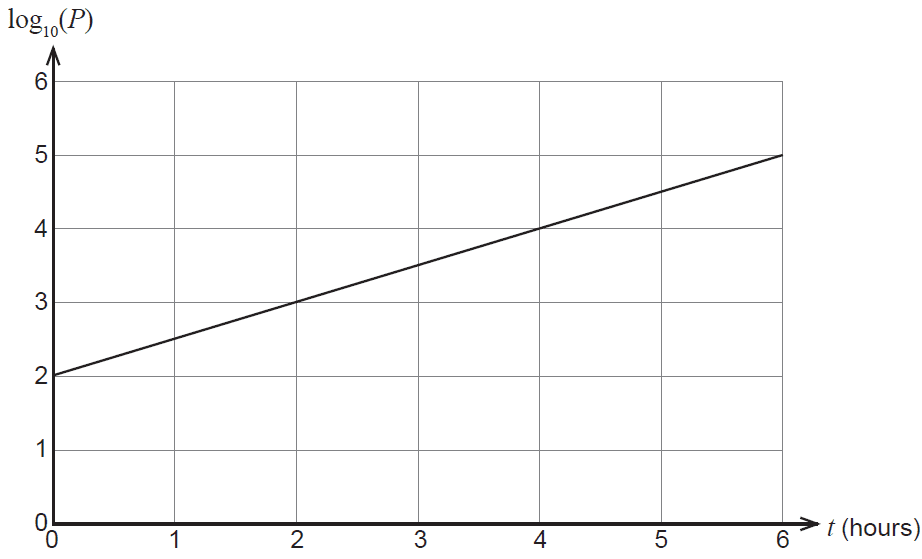
(a)

(i) On the basis of the graph above, what is the size of the bacteria population after two hours? (2 marks)

(ii) The equation of the line can be written in the form \(\log_{10}(P) = At + B\). Use the graph to determine the values of \(A\) and \(B\). (2 marks)

Another population of the same bacteria is cultured at 40 °C. The size of the population, \(P\), after \(t\) hours satisfies the equation

\[ \log_{10}(P) = \frac{1}{3}t + 2. \]

(b)

(i) Express the above equation in the form \(P = A(10)^{Bt}\). (3 marks)

(ii) Determine the size of the population after exactly four hours to the nearest whole number. (1 mark)

(iii) Express the above equation in the form \(t = C\log_{10}\left(\frac{P}{D}\right)\). (3 marks)

(iv) How many minutes does it take for the population to reach a size of 5000? Give your answer to the nearest minute. (2 marks)

(c) With reference to parts (a) and (b), describe the effect of temperature on the population growth of this type of bacteria. (2 marks)

Question 18 (9 marks) [2019 Section 2 Q18]

A building has five alarms configured in such a way that the system functions if at least two of the alarms work. The probability that an alarm fails overnight is 0.05. Let the random variable \(\hat{X}\) denote the number of alarms that fail overnight.

(a) State the distribution of \(\hat{X}\). (2 marks)

(b) What assumptions are required for the distribution in part (a) to be valid? (2 marks)

(c) What is the probability that the alarm system fails overnight? (2 marks)

One of the alarms is removed in the evening for maintenance and is not replaced.

(d) What is the probability that the alarm system still works in the morning? (3 marks)