Question 1 (5 marks) [2017 Section 1 Q1]

Anastasia is a university student. She records the time it takes for her to get from home to her campus each day. The histogram of relative frequencies below shows the journey times she recorded.

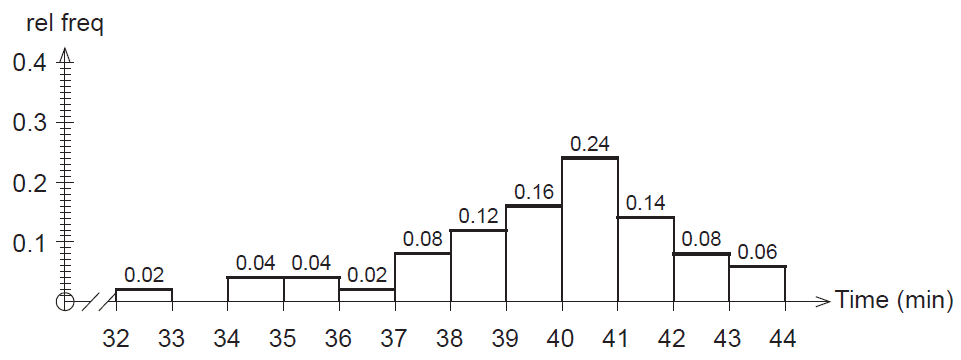
Use the above data to estimate the probability of her next journey from home to her university campus

(a) taking her less than 36 minutes. (1 mark)

(b) taking at least 35 minutes but no more than 39 minutes. (2 marks)

On three consecutive days, Anastasia needs to be on campus no later than 10 am.

(c) If she leaves her home at 9:22 am each day, use the above data to estimate the probability that she makes it on or before time on all three days. (2 marks)

Question 2 (6 marks) [2017 Section 1 Q2]

Michelle is a soccer goalkeeper and has built a machine to help her practise. The machine will shoot a soccer ball randomly along the ground at or near a goal that is seven metres wide. The machine is equally likely to shoot the ball so that the centre of the ball crosses the goal line anywhere between point A three metres left of the goal, and point B five metres right of the goal, as shown in the diagram below.

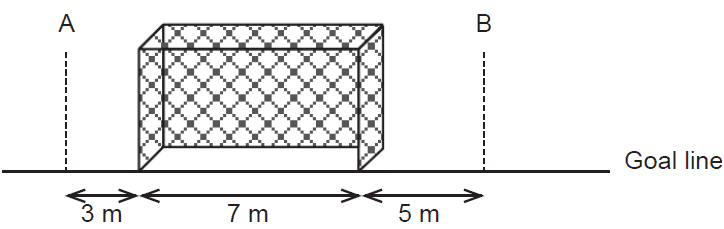
Michelle sets up a trial run without anyone in the goals. Assume the goal posts are of negligible width.

Let the random variable \(X\) be the distance the centre of the ball crosses the goal line to the right of point A.

(a) Complete the graphical representation of the probability density function for the random variable \(X\). (2 marks)

(b) What is the probability that the machine shoots a ball so that its centre misses the goal to the left? (1 mark)

(c) What is the probability that the machine shoots a ball so that its centre is inside the goal? (1 mark)

(d) If the machine shoots a ball so that its centre misses the goal, what is the probability that the ball's centre misses to the right? (2 marks)

Question 3 (4 marks) [2017 Section 1 Q3]

Solve \(4e^{2x} = 81 - 5e^{2x}\) exactly for \(x\).

Question 4 (3 marks) [2017 Section 1 Q4]

Two independent samples of different sizes were taken from a population. The first sample had sample size \(n_1\) and the second sample had sample size \(n_2\). The sample proportions of males in the samples were the same. When 99% confidence intervals were calculated for each sample, it was found that the corresponding margin of error in the second sample was half that of the first sample.

What is the ratio of the two sample sizes, \(\frac{n_2}{n_1}\)?

Question 5 (8 marks) [2017 Section 1 Q5]

(a) Consider the shaded area shown between the graph of \(y=e^x\), the y axis and the line \(y=2\).

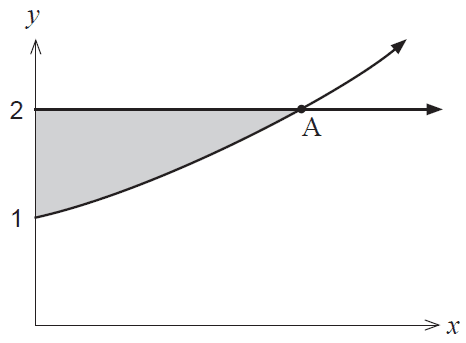
(i) Determine the coordinates of the point A. (1 mark)

(ii) Hence or otherwise determine the area between the graph of \(y=e^x\), the y axis and the line \(y=2\). (3 marks)

(b) If the area between the graph of \(y=e^x\), the y axis, the x axis and the line \(x=k\), where \(k \ge 0\), is to be equal to 2 square units, determine the exact value of \(k\). (4 marks)

Question 6 (7 marks) [2017 Section 1 Q6]

(a) Evaluate \(\int_{0}^{1} \frac{-12x}{1+3x^2} dx\). (3 marks)

(b) Given \(f(x) = \ln(2-x^3)\)

(i) determine \(f'(1)\). (3 marks)

(ii) In relation to the graph of \(f(x)\), explain the meaning of your answer to (b)(i). (1 mark)

Question 7 (6 marks) [2017 Section 1 Q7]

Given that \(\log_{10}2 = x\) and \(\log_{10}7 = y\)

(a) express \(\log_{10}14\) in terms of \(x\) and \(y\). (2 marks)

(b) show that \(\log_{10}17.5 = y - 2x + 1\). (2 marks)

(c) evaluate \(10^{y-x}\). (2 marks)

Question 8 (5 marks) [2017 Section 1 Q8]

(a) Differentiate \(2x\sin(3x)\) with respect to \(x\). (2 marks)

(b) Hence show that \(\int x \cos(3x) dx = \frac{3x \sin(3x) + \cos(3x)}{9} + c\). (3 marks)

Question 9 (8 marks) [2017 Section 1 Q9]

Consider the function \(f(x)\) shown graphed below. The table gives the value of the function at the given \(x\) values.

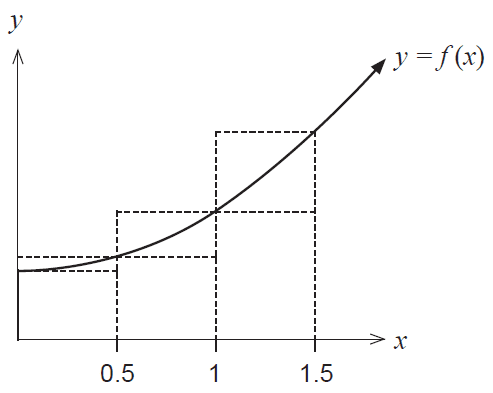
\(x\)	0	0.5	1	1.5
\(f(x)\)	20	21	24	29

(a) By considering the areas of the rectangles shown, demonstrate and explain why

\[ 32.5 < \int_0^{1.5} f(x) dx < 37 \] (3 marks)

Consider the table of further values of \(f(x)\) given below.

\(x\)	0	0.5	1	1.5	2	2.5	3
\(f(x)\)	20	21	24	29	36	45	56

(b) Use the table values to determine the best estimate possible for \(\int_1^3 f(x)dx\). (3 marks)

(c) State two ways in which you could determine a more accurate value for \(\int_1^3 f(x)dx\). (2 marks)

Question 10 (3 marks) [2017 Section 2 Q10]

Use the quotient rule to show that \( \frac{d}{dx} \tan(x) = \frac{1}{\cos^2(x)} \).

Question 11 (9 marks) [2017 Section 2 Q11]

A pizza shop estimates that the time \(X\) hours to deliver a pizza from when it is ordered is a continuous random variable with probability density function given by

\[ f(x) = \begin{cases} \frac{4}{3} - \frac{2}{3}x, & 0 < x < 1 \\ 0, & \text{otherwise.} \end{cases} \]

(a) What is the probability of a pizza being delivered within half an hour of being ordered? (2 marks)

(b) Calculate the mean delivery time to the nearest minute. (3 marks)

(c) Calculate the standard deviation of the delivery time to the nearest minute. (4 marks)

Question 12 (13 marks) [2017 Section 2 Q12]

The Slate Tablet Company produces a variety of electronic tablets. It wants to gather information on consumers' interest in its tablets.

(a) In each of the following cases, comment, giving reasons, whether or not the proposed sampling method introduces bias.

(i) A Slate Tablet Company representative stood outside an electronics store on a Saturday morning and asked people entering the store 'If you were to purchase an electronic tablet would you choose a Slate Tablet or an inferior brand?' (2 marks)

(ii) Fifteen hundred randomly selected mobile phone numbers were telephoned and people were asked 'Which brand of electronic tablet do you prefer?' (2 marks)

A common problem with a particular tablet is screen failure. The manufacturer of Slate Tablets has found that 1% of its tablet screens will fail within three years. A sample of 200 tablets is taken. Let the random variable \(\hat{X}\) denote the number of tablets that have screen failure within three years in the sample of 200.

(b) What is the distribution of \(\hat{X}\)? (2 marks)

(c) What is the probability that more than four tablets will have screen failure within three years? (2 marks)

In a random sample of 200 Slate Tablets, four of them had screen failure within three years.

(d) Calculate an approximate 95% confidence interval for the proportion of tablets that have screen failure within three years. Give your answer to four decimal places. (3 marks)

(e) The company's quality control department wants the proportion of tablets with faulty screens to be between 0.5% and 1%. Based on your confidence interval, decide whether the quality control department is meeting its target. Justify your decision. (2 marks)

Question 13 (9 marks) [2017 Section 2 Q13]

Ravi runs a dice game in which a player throws two standard six-sided dice and the sum of the uppermost faces is calculated. If the sum is less than five, the player wins $20. If the sum is greater than eight, the player wins $10. Otherwise the player receives no money.

(a) Complete the table below. (2 marks)

Amount won
Probability

(b) What is the expected amount of money won by a player each time they play? (2 marks)

(c) Liu Yang decides to play the game. If Ravi charges her $5 to roll two dice, who is likely to be better off in the long-term? Explain. (3 marks)

(d) If Ravi wants to make a long-term profit per game of 20% of what he charges, what should he charge a player to roll the two dice? (2 marks)

Question 14 (9 marks) [2017 Section 2 Q14]

Let \(f(x) = x \ln(x+3)\).

(a) Use calculus to locate and classify all the stationary points of \(f(x)\) and find any points of inflection. (5 marks)

(b) On the axes provided sketch the graph of \(f(x)\), labelling all key features. (4 marks)

Question 15 (10 marks) [2017 Section 2 Q15]

The volume \(V(h)\) in cubic metres of a liquid in a large vessel depends on the height \(h\) (metres) of the liquid in the vessel and is given by

\[ V(h) = \int_0^h e^{\frac{x^2}{100}} dx, \quad 0 \le h \le 15. \]

(a) Determine \(\frac{dV}{dh}\) when the height is 0.5 m. (2 marks)

(b) What is the meaning of your answer to part (a)? (1 mark)

(c) The height of the liquid depends on time \(t\) (seconds) as follows: \(h(t) = 3t^2 - t + 4, t \ge 0\).

(i) Determine \(\frac{dh}{dt}\) when the height is 6 m. (2 marks)

(ii) Use the chain rule to determine \(\frac{dV}{dt}\) when the height is 6 m. (2 marks)

(iii) Given the volume of the liquid at 2 seconds is 8.439 m³, use the incremental formula to estimate the volume 0.1 second later. (3 marks)

Question 16 (8 marks) [2017 Section 2 Q16]

A group of biologists has decided that colonies of a native Australian animal are in danger if their populations are less than 1000. One such colony had a population of 2300 at the start of 2011. The population was growing continuously such that \(P = P_0 e^{0.065t}\) where \(P\) is the number of animals in the colony \(t\) years after the start of 2011.

(a) Determine, to the nearest 10 animals, the population of the colony at the start of 2014. (2 marks)

(b) Determine the rate of change of the colony's population when \(t = 2.5\) years. (2 marks)

(c) At the beginning of 2017, a disease caused the colony's population to decrease continuously at the rate of 8.25% of the population per year. If this rate continues, when will the colony become 'in danger'? Give your answer to the nearest month. (4 marks)

Question 17 (6 marks) [2017 Section 2 Q17]

A beverage company has decided to release a new product. 'Joosilicious' is to be sold in 375 mL cans that are perfectly cylindrical. {Hint: 1 mL = 1 cm³}

(a) If the cans have a base radius of \(x\) cm show that the surface area of the can, \(S\), is given by: \( S = 2\pi x^2 + \frac{750}{x} \). (2 marks)

(b) Using calculus methods, and showing full reasoning and justification, find the dimensions of the can that will minimise its surface area. (4 marks)

Question 18 (11 marks) [2017 Section 2 Q18]

Alex is a beekeeper and has noticed that some of the bees are very sleepy. She takes a random sample of 320 bees and finds that 15 of them are indeed so-called lullabees that fall asleep easily.

(a) Calculate the sample proportion of lullabees. (1 mark)

(b) Determine a 90% confidence interval for the true proportion of lullabees, rounded to four decimal places. (3 marks)

(c) What is the margin of error in the above estimate? (2 marks)

It turns out that the true proportion of lullabees is 0.02.

(d) Now that Alex knows this, she decides to take a new sample.

(i) Suppose a new sample of 290 bees was taken. Given that the true proportion of lullabees is 0.02, what is the probability that the sample proportion in this new sample is at most 0.03? (3 marks)

(ii) If Alex takes a larger sample, will the above probability increase or decrease? Explain. (2 marks)

Question 19 (12 marks) [2017 Section 2 Q19]

A global financial institution transfers a large aggregate data file every evening from offices around the world to its Hong Kong head office. Once the file is received it must be processed in the company's data warehouse. The time \(T\) required to process a file is normally distributed with a mean of 90 minutes and a standard deviation of 15 minutes.

(a) An evening is selected at random. What is the probability that it takes more than two hours to process the file? (2 marks)

(b) What is the probability that the process takes more than two hours on two out of five days in a week? (3 marks)

The company is considering outsourcing the processing of the files.

(c)

(i) A quotation for this job from an IT company is given in the table below. Complete the table. (1 mark)

Job duration (minutes)	\(T \le 60\)	\(60 < T < 120\)	\(T \ge 120\)
Probability
Cost \(Y\) ($)	200	600	1200

(ii) What is the mean cost? (2 marks)

(iii) Calculate the standard deviation of the cost. (2 marks)

(iv) In the following year, the cost (currently \(\$Y\)) will increase due to inflation and also the introduction of an additional fixed cost, so the new cost \(\$N\) is given by: \(N=aY+b\). In terms of \(a\) and/or \(b\), state the mean cost in the following year and the standard deviation of the cost in the following year. (2 marks)

Question 20 (9 marks) [2017 Section 2 Q20]

A model train travels on a straight track such that its acceleration after \(t\) seconds is given by \(a(t) = pt - 13\) cm/s², \(0 \le t \le 10\), where \(p\) is a constant.

(a) Determine the initial acceleration of the model train. (1 mark)

The model train has an initial velocity of 5 cm/s. After 2 seconds it has a displacement of -50 cm. A further 4 seconds later its displacement is 178 cm.

(b) Determine the value of the constant \(p\). (4 marks)

(c) When is the model train at rest? (2 marks)

(d) How far has the model train travelled when its acceleration is 47 cm/s²? (2 marks)